Conway's card game problem has finally been solved

Created: January 21, 2025
Updated: January 27, 2025

Introduction

There are few events in mathematical folklore more renown than when David Hilbert introduced his famous list of unsolved problems at the turn of the 19th century. He hoped that this list, containing 23 questions unresolved by 19th century mathematics, would focus the efforts of of mathematicians over the next millennium. Among them are problems that have greatly informed the course of mathematics, like the search for a rigorous foundation for arithmetic, the continuum hypothesis and the Riemann hypothesis.

But much less well known is a list of problems due to another famous mathematician, John Conway. He kept a private list of what he called his “anti-Hilbert problems”, writing in a private email exchange that:

“Hilbert’s were some problems for mathematicians to work on during this century. Mine are problems we should NOT be working on during the next.”

Although no complete list of his anti-Hilbert problems can be found, known to be among them is a simple question about an old card game called “Beggar-my-neighbour”.

This problem, solved in March 2024, is a unique example of a semi-obscure problem which is simple enough to explain to a child, yet whose solution withstood several decades of rigorous attack. In this post, I’ll explain the game and the problem itself, some reasons for why it was so difficult to solve, and go through the broad strokes that the researchers took to finally reach a solution.

The game

Beggar-my-neighbour, also known by more a collection of more violent names like “beat your neighbour” or “beat jack out of doors”, is played as follows:

  • Setup: A full pack of 52 cards is dealt to two players, and they keep their cards face-down on a table.

  • Play: The first player turns over the card at the top of their pack and places it in the middle. If the card is a number card (i.e. has value from 2 through 10), then nothing happens and the second player places down their card in the middle. Play alternates like this as long as no face card (i.e. an ace, jack, queen or a king) appears.
  • If a face card does appear, then the other player has to “pay” for it by placing down several of their cards: 4 for an ace, 3 for a king, 2 for a queen and 1 for a jack. Once they’ve placed these cards down, the player who initially dealt the face card collects the pack of cards which has collected in the middle and adds it to the bottom of their deck.

  • However, if the other player places down a face card while they are paying, the play switches, and the other player must instead pay the other player for the value of that face card.

  • Ending: Once a player turns over their last card, the game ends, and the winner is the player holding the whole deck.

This game has been around a very long time – it appears explicitly in Charles Dickens’ “Great Expectations”, but might even be 100 years older than that. You can try the game for yourself here. Note that at each stage each player has exactly one move, and so the game is completely determined by the initial deal.

Example game

Here’s an example game. The initial cards have been dealt and the middle of the table is empty.

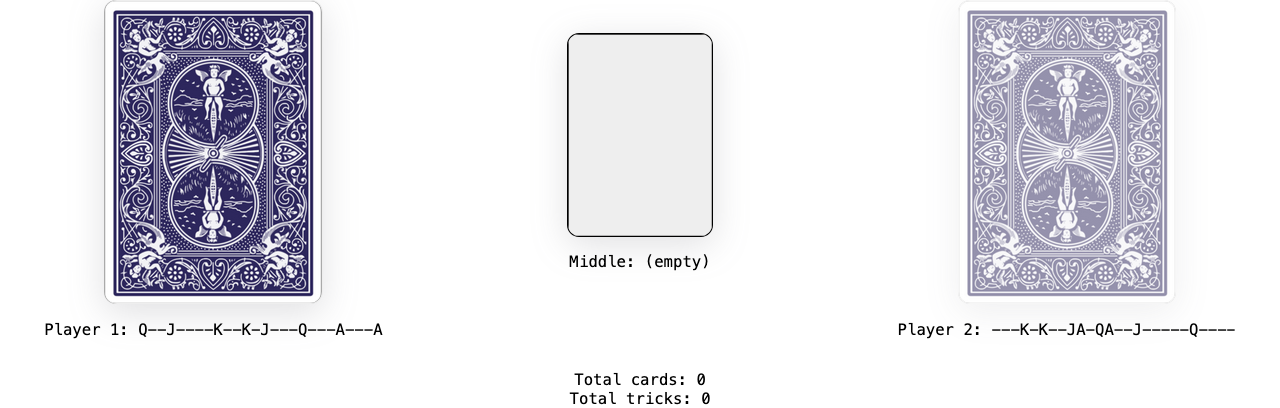
I’m showing the contents of each players’ hands here but in a real game, these would be kept hidden. Since the values of the non-face cards don’t matter, here they’re just denoted with a -, and the suit information is irrelevant to the game so each face card is just ace (A), king (K), queen (Q) or jack (J).

Player 1 goes first and turns over the top card, placing it in the middle of the table.

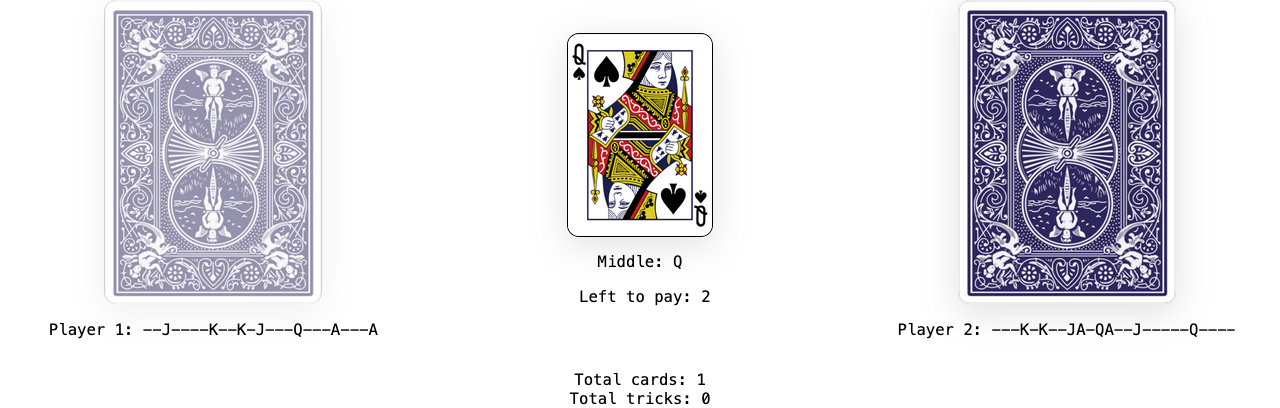
Now the second player has to place down two of their cards in order to pay for it. Since neither of these are face cards, they finish paying and the first player wins that trick and these cards get added to the first player’s hand.

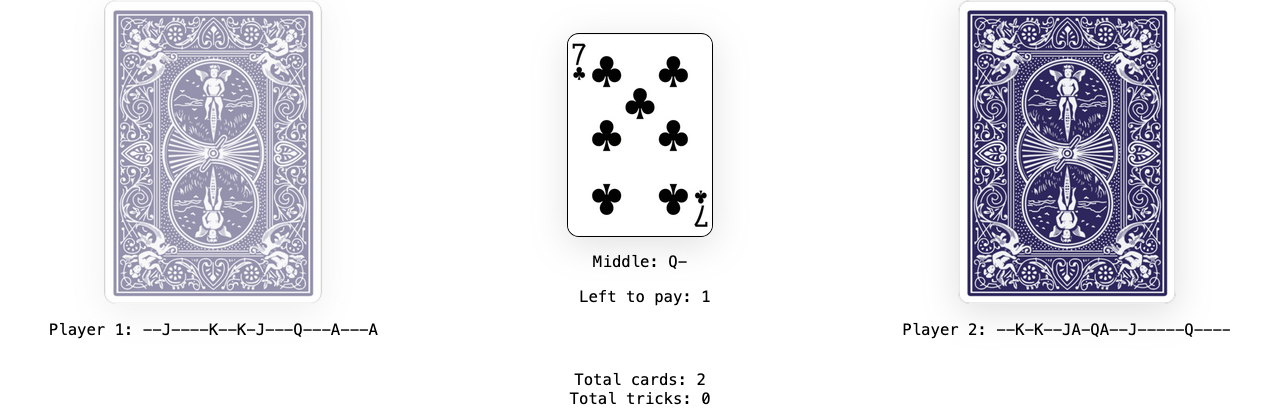
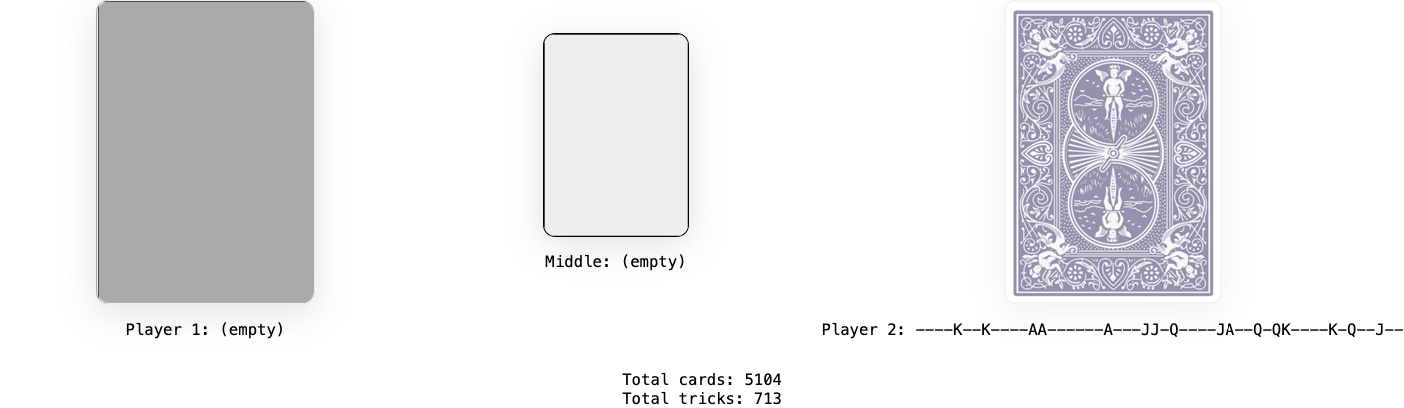
Play continues like this, with the first player going first since they won the last set of cards. After several more iterations, the state of the game looks like this:

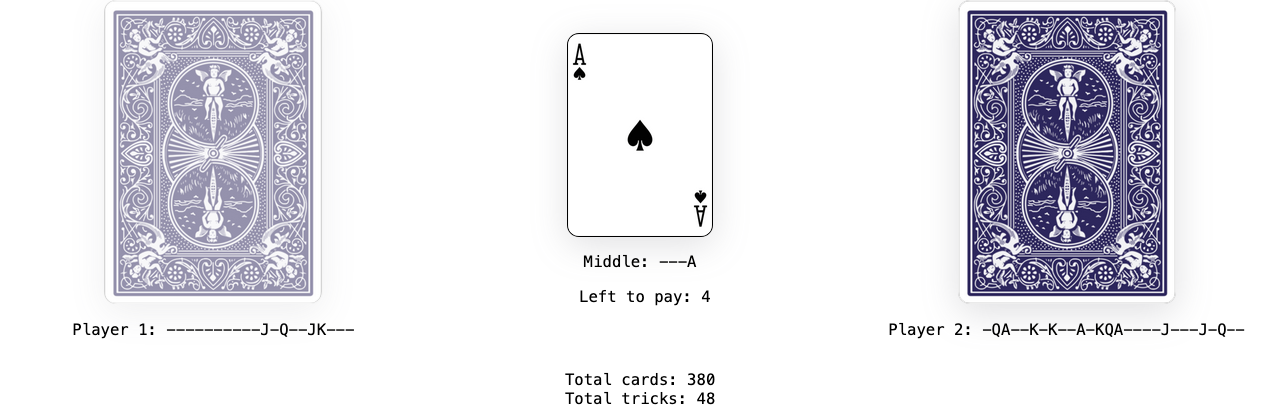
The game continues until one player uses all their cards. This game, found by computer search, ends up taking a very long time but is eventually a win for the second player:

The problem

Once you’ve played this game for a while, it becomes apparent that some games last for longer than others, but every game seems to end eventually. It is therefore a very natural question to ask:

Is there a game of beggar-my-neighbour goes on forever?

Richard Guy, one of Conway’s close collaborators wrote about the game: “This problem reappears periodically. It was one of Conway’s ‘anti-Hilbert problems’ about 40 years ago, but must have suggested itself to players of the game over the several centuries of its existence”. Now, 60 years after it was posed, this problem has finally been solved in the positive by a group of 8 researchers explicitly constructing a non-terminating game, spearheaded by

Some reasons for pessimism

How would you go about answering this problem? One approach is just to get a computer to play out lots of games, and this is precisely what people did in the first few decades of this problem’s existence.

A quick back-of-the-envelope calculation shows that there are

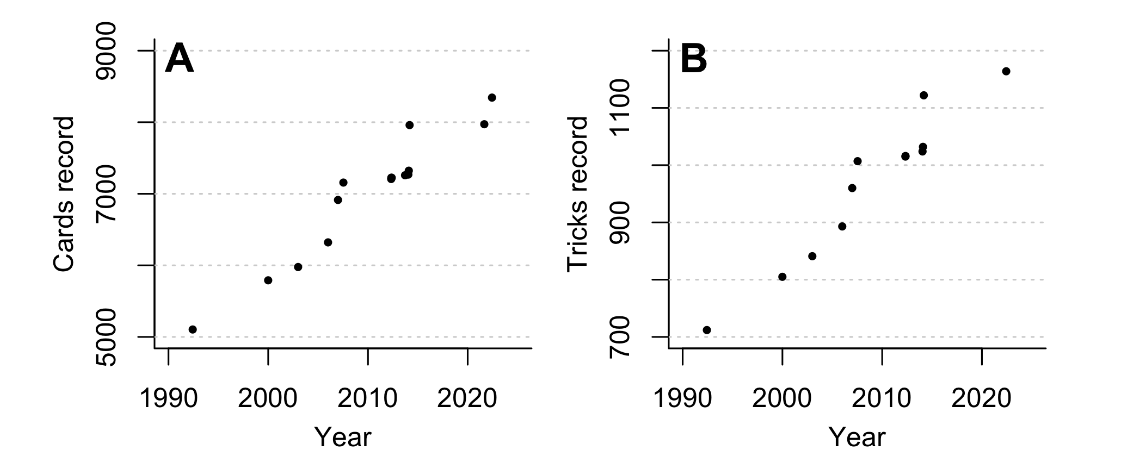
\[{52 \choose 4} {48 \choose 4} {44 \choose 4} {40 \choose 4} \approx 6.54 \times 10^{20}\]

possible starting configurations, ignoring details irrelevant to the outcome of the game. While this number is huge – if you could check each game for termination in one nanosecond, it would take 20,000 years to check every configuration – you might hope that the relative frequency of looping games is high enough that you only need to search through a small portion of these games before getting a hit.

But alas, this turned out to not be the case. Over several years, many people found starting hands which went on for longer and longer, but none that formed cycle. Clearly a different approach was needed. Indeed, before this non-terminating game was constructed, on the order of $10^{13}$ games had been checked; eating up significant compute.

One way to think about searching through this game tree is by imagining an astronomical mess of tangled computer cables many millions of years across. The cables are tightly interconnected, branching and converging. Somewhere, deep in the tangle, there might be one cable with its two ends connected. Finding a looping configuration by random search is like shaking the mess and seeing what falls out, hoping that it is what you happen to be looking for. But given that this was tried for several years without success means that a more clever approach was necessary.

Another reason to be pessimistic is the possibility that there are no looping games whatsoever, and that any search is going to fail. This is not so much of a remote possibility: it’s possible to consider variants of the game (e.g. less than 52 cards, no aces, and so on) which are amenable to brute-force search, and for some of these it can be checked that no looping configuration exists.

But there is something exciting about the idea of running your own search and getting lucky finding a looping game, or at the very least, finding a game that goes on for longer than all previous records. Perhaps this is why Conway designated this problem as one of his “anti-Hilbert” problems – it seems like the problem is a huge time and compute sink, the equivalent of playing a computational lottery.

Finding a needle in a haystack

Given this, how was a looping game found by researchers in early 2024? Rather than simulating trillions of games on a computer, the researchers used several clever tricks to whittle down their search so that in the end it was much less random but more like gently coaxing a cycling game out of the game tree.

I won’t cover the details here since the paper itself does a very good job of explaining how they arrived at their non-terminating game. But the general observations that lead to the solution were:

  • While some variants have no non-terminating games, a few variants do have non-terminating games. For example, J--/-J- is a terminating game over a deck with just six cards and two jacks.
  • It’s possible to expand non-terminating games over smaller decks to larger decks, e.g. by doubling up each hand: J--J--/-J--J-.
  • If you drop the condition that the starting hands must have the same number of cards for both players, then it’s possible to find unbalanced non-terminating games, and then you can play through the game to see if it becomes balanced at any point in the cycle.
  • While there was direct finds with this approach, the unbalanced non-terminating games that were found had a certain structure which allowed the researchers to guess that there would be a balanced non-terminating game which had a particular shape.
  • Running another search for games with this particular shape eventually yielded a non-terminating game.

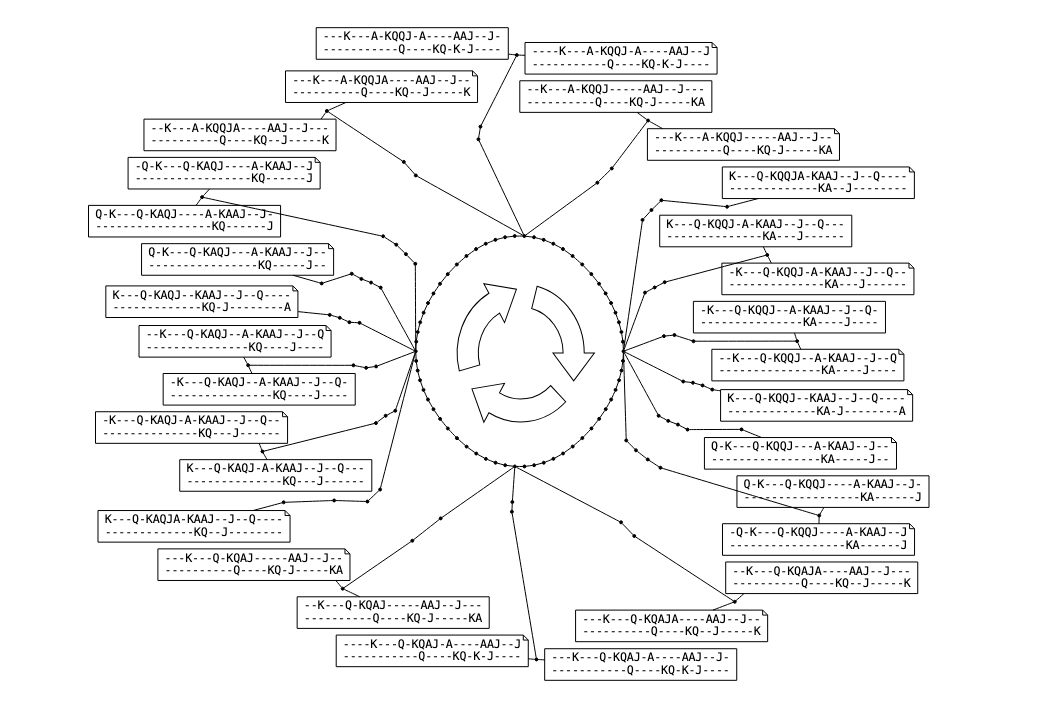
Here it is, the culmination of several decades of work:

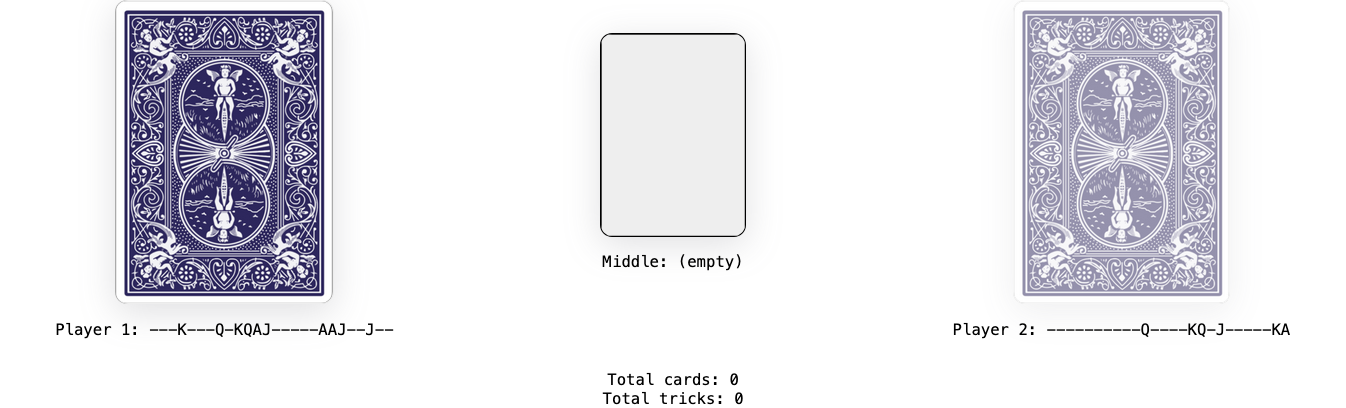
Since the game does enter a cycle, by searching backwards for balanced hands at different points in the loop, they actually found a family of non-terminating games. Each large box is a possible starting state, and the dog-eared boxes are games where the second player should start rather than the first player.

Conclusion

John Conway passed away in 2020 but his legacy lives on in his results, creations and problems. This particular problem was just one in a zoo of mathematical curiosities that he and his collaborators built over their lifetimes, and there are many other problems, some solved, and some not:

And while the researchers solved the biggest problem concerning beggar-my-neighbour, there are still many more questions you could ask. They themselves suggest several in the paper:

  • How many cycles are there in the game tree?
  • How many non-terminating games exist?
  • What is the longest possible terminating game?

There’s good arguments that these questions are probably even more difficult to answer than finding a non-terminating game, but they’re definitely questions for 21st mathematics to chew on.

References



Related posts