Winning colourful Nim with the eeny-meeny rule
A more detailed version of this is now available as a PDF. This now includes a proof that the eeny-meeny rule is correct for any $k$!
Colourless Nim
Nim is a game where two players take turns removing (“nimming”) stones from different piles. On each player’s turn, they can remove as many stones as they like, but they all have to be from one pile. The player who makes the last move wins – or equivalently, the player who is left with no remaining moves loses.
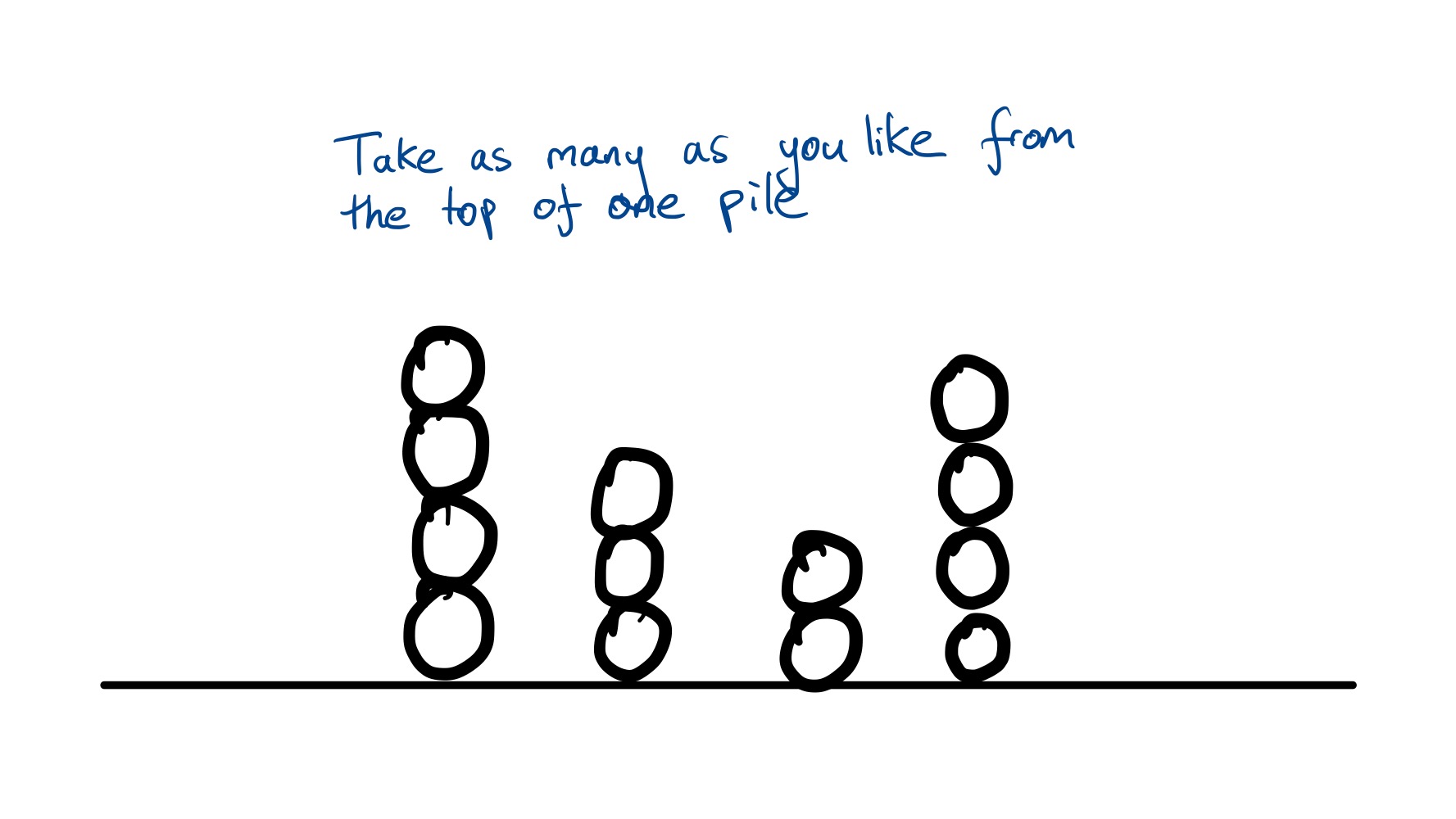
This simple game turns out to run surprisingly deep in the field of mathematics known as combinatorial game theory, which is concerned for the most part with beating opponents at two-player perfect information games, like tic-tac-toe, checkers and Go. Specifically, there’s a result called the Sprague-Grundy theorem which states (informally) that every combinatorial game where each player has access to the same set of moves on each of their turns is equivalent to a game of Nim. Combinatorial games like this are called “impartial games”.
This means the following – if you’re playing an impartial game, and:
- You are a perfect Nim player, and
- You know how to convert positions in this game into an game of Nim
…then you can always win at that impartial game.
Luckily, perfect play at Nim is reasonably easy if you know the trick, a result called Bouton’s theorem, which says that you can always guarantee a win if, on your turn, you remove stones to make the bitwise XOR (sometimes called the nim-sum) of all the pile sizes equal to $0$.
Mentally calculating the bitwise XOR of lots of numbers sounds difficult, but it is surprisingly simple.
Colourful Nim
Now suppose you’re playing the game with a set of English pool balls which are red and yellow, and you add the rule that you can only remove sections of contiguous colour from the tops of each pile:

You could also play this game with cards facing up and down, knives and forks, bananas and apples, and so on. You just need two distinguishable items you can make piles out of.
If you want to try it out online, you can play it here.
The winning strategy for just one pile is reasonably straightforward to work out (consider which moves you can force your opponent to take). But when there are multiple piles, things are a lot more interesting and working out the best move is non-trivial.
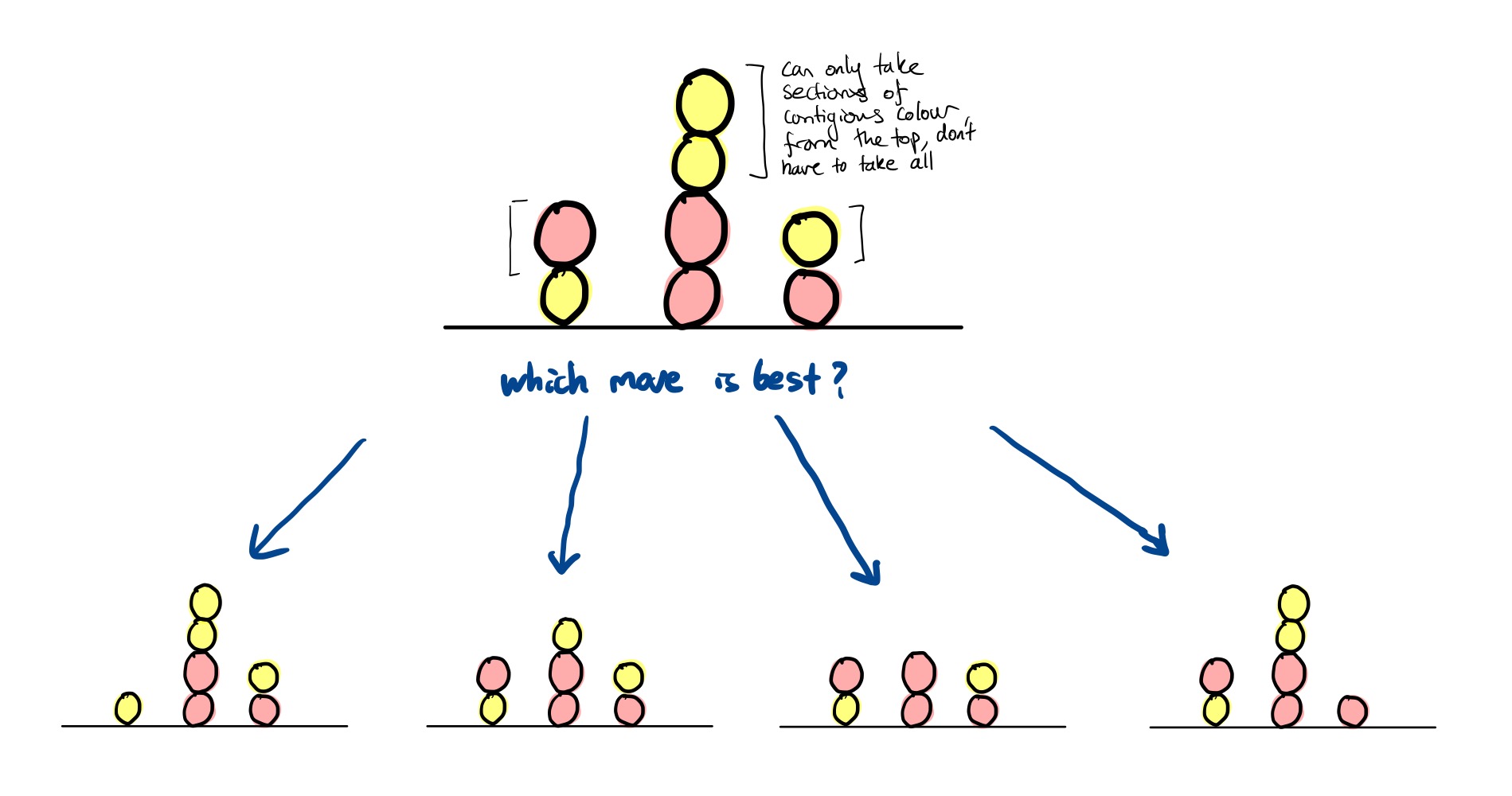
A (possible) winning strategy for multiple piles
The following gives the perfect strategy for any number of piles.
…or at least I’m 99% sure it does. I haven’t succeeded in proving the strategy is correct for any number of piles and any number of colour changes, but have done so when there are any number of piles, each of which has at most 4 colour changes.
To describe the winning strategy, we’ll need some notation.
Notation: Write $(n _ 1, \ldots, n _ k)$ for a pile with $n _ k$ balls of one colour at the top, followed by $n _ {k-1}$ balls of the next colour, followed by $n _ {k-2}$ of the original colour, and so on, all the way until $n _ 1$ which gives the number of balls in the bottom section of the pile.
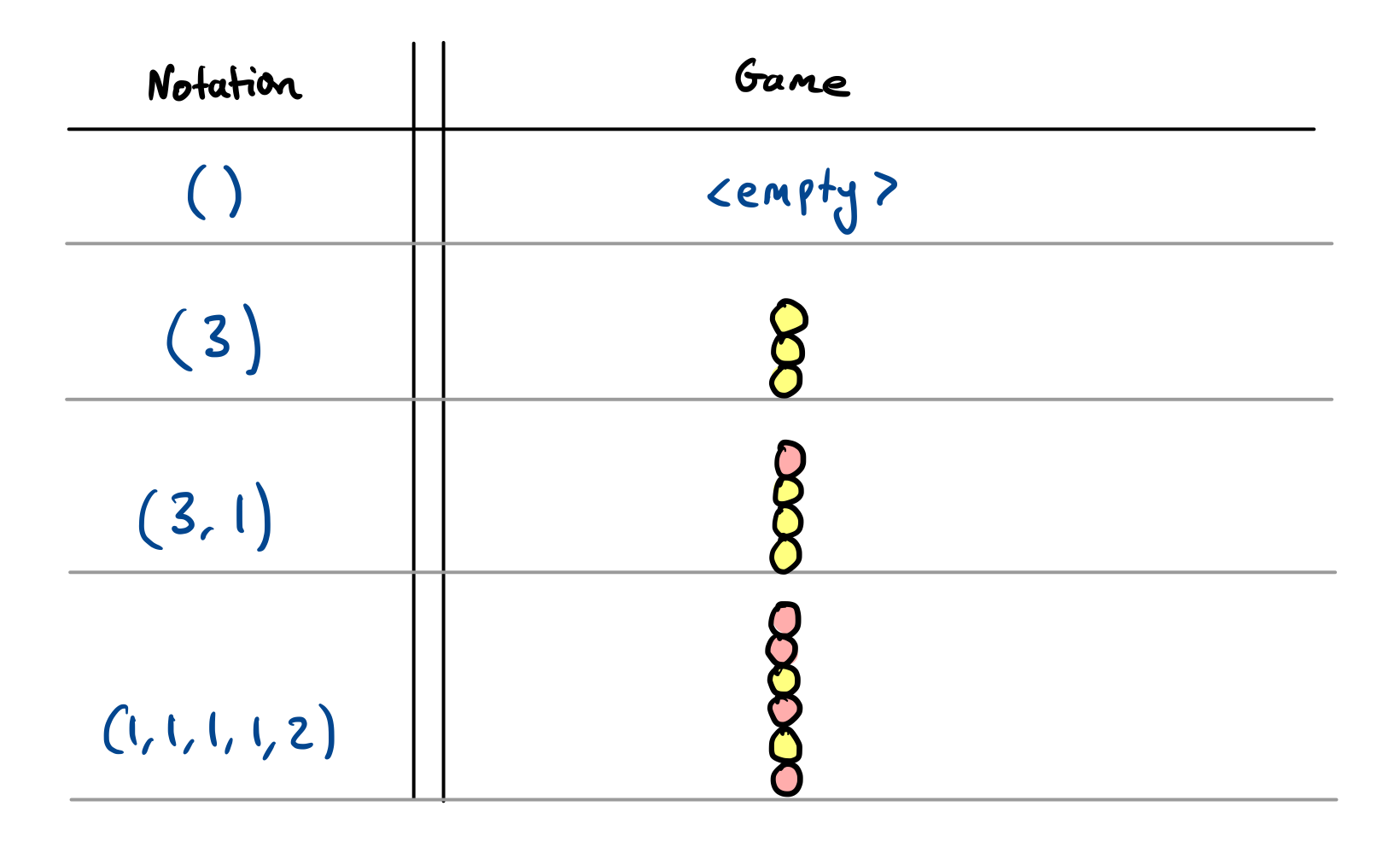
Note that for all practical purposes when trying to win, it doesn’t matter if the pile starts yellow or starts red, it is really only the sequence of colour changes that matters.
The strategy is almost identical to ordinary Nim. In ordinary Nim, you win by making the XOR of all the pile sizes equal to zero. Now instead of making the XOR of all the pile sizes equal to zero, you make the XOR of the “Grundy values” of each pile equal to zero. Write $\mathcal G(n _ 1, \ldots, n _ k)$ for the Grundy value of the pile $(n _ 1, \ldots, n _ k)$.
It’s not necessary to know exactly what “Grundy value” means to win, we just need to know how to calculate it. But intuitively, the Grundy value of a pile tells you the size of the equivalent Nim heap as guaranteed to exist by the Sprague-Grundy theorem.
The empty game has Grundy value $0$, or in the notation, $\mathcal G() = 0$. If the pile is just of one colour, then the Grundy value is just the number of balls in that pile. In our notation, this means $G(n _ 1) = n _ 1$. This makes sense, a pile with no colour changes is equivalent to a game of Nim.
To calculate the Grundy value for piles with colour changes, things get a bit more complicated. To do this, you need the “eeny-meeny rule”.
The eeny-meeny rule
Say you’re looking at a pile $(n _ 1, \ldots, n _ k)$. The rule is:
\[\mathcal G(n_1, \ldots, n_k) = \begin{cases} n_k - 1 &\text{if the eeny-meeny condition is met} \\ n_k &\text{otherwise} \end{cases}\]So either $\mathcal G(n _ 1, \ldots, n _ k)$ is $n _ k$ or $n _ k-1$, and the eeny-meeny condition tells you if you need to subtract one. When is the eeny-meeny condition met?
- Start by looking at the top of the pile, $n _ k$, and work your way down each section of colour in steps, saying “eeny” and “meeny” alternately.
- Call $n _ k$ eeny compared to $n _ {k-1}$ if $n _ k < n _ {k-1}$ (exiguous, very small in size or amount).
- Call $n _ {k}$ meeny compared to $n _ {k-1}$ if $n _ k > n _ {k-1}$ (massive, large and heavy or solid).
- If you say “eeny” moving from $n _ k$ to $n _ {k-1}$ and $n _ k$ is eeny compared to $n _ {k-1}$ (i.e. $n _ k < n _ {k-1}$), then the condition is met! You should subtract one, so $\mathcal G(n _ 1, \ldots, n _ k) = n _ k - 1$ in this case.
- If you say “meeny” moving from $n _ k$ to $n _ {k-1}$ and $n _ k$ is meeny compared to $n _ {k-1}$ (i.e. $n _ k > n _ {k-1}$), then the condition is also met! You should subtract one, so $\mathcal G(n _ 1, \ldots, n _ k) = n _ k - 1$ in this case.
- If $n _ k = n _ {k-1}$, continue working your way down the pile.
- If $n _ k$ is meeny compared to $n _ {k-1}$ when it is supposed to be eeny or $n _ k$ is eeny compared to $n _ {k-1}$ when it is supposed to be meeny, then you can stop checking. The condition is not met, and you can stop looking.
- …
- There is one more special case: if you say eeny as you reach the end of the pile, then $n _ 2$ can be eeny compared $n _ 1$ with equality, so $n _ 2 \le n _ 1$ is a valid comparison.
In more mathematical notation, you’re applying the two formulas:
\[\mathcal{G}(n_1, \ldots, n_{2k}) = \begin{cases} n_{2k}-1 &\text{if }&& n_{2k} < n_{2k-1}, \text{ or} \\ & &&n_{2k} = n_{2k-1} > n_{2k-2}, \text{ or} \\ & && \quad\quad\quad\quad\quad\quad\vdots\\ & &&n_{2k} = n_{2k-1} = n_{2k-2} < n_{2k-3} \\ &\ldots\text{until}\ldots &&n_{2k} = n_{2k-1} = \cdots = n_2 > n_1 \\ \\ n_{2k} &\text{otherwise} && \end{cases}\]in the even case, and
\[\mathcal{G}(n_1, \ldots, n_{2k-1}) = \begin{cases} n_{2k-1}-1 &\text{if }&& n_{2k} < n_{2k-1}, \text{ or} \\ & &&n_{2k} = n_{2k-1} > n_{2k-2}, \text{ or} \\ & && \quad\quad\quad\quad\quad\quad\vdots\\ & &&n_{2k} = n_{2k-1} = n_{2k-2} < n_{2k-3} \\ &\ldots\text{until}\ldots &&n_{2k} = n_{2k-1} = \cdots = n_2 \le n_1 \\ \\ n_{2k-1} &\text{otherwise} && \end{cases}\]in the odd case. Or, an equivalent Python program is the following:
def eeny_meeny(pos):
# Assumes `pos` is a list like [n_1, ..., n_k].
# For an empty pile, the value is zero.
if len(pos) == 0:
return 0
# For a single-coloured pile, the value is just the
# number of balls.
if len(pos) == 1:
return pos[0]
# Get the value at the top of the pile
n_k = pos[-1]
# Work out if the eeny-meeny condition is met
condition_met = False
state = "eeny"
i = len(pos) - 1
while i >= 1 and not condition_met:
n = pos[i]
n_next = pos[i-1]
if state == "eeny":
if n < n_next: # n is eeny compared to n_next
condition_met = True
elif i == 1 and n <= n_next: # special case for eeny end
condition_met = True
elif n == n_next: # Keep going if equal
pass
elif n > n_next: # meeny when its supposed to be eeny
break
if state == "meeny":
if n > n_next: # n is meeny compared to n_next
condition_met = True
elif n == n_next: # Keep going if equal
pass
elif n < n_next: # eeny when its supposed to be meeny
break
state = "eeny" if state == "meeny" else "meeny" # Flip the state
i -= 1
if condition_met:
return n_k - 1
else:
return n_k
This looks quite complicated, but it is just a rule that lets you work out whether the Grundy value is the number of balls in the top section, or that number minus one. Here are some illustrations.
Example calculations
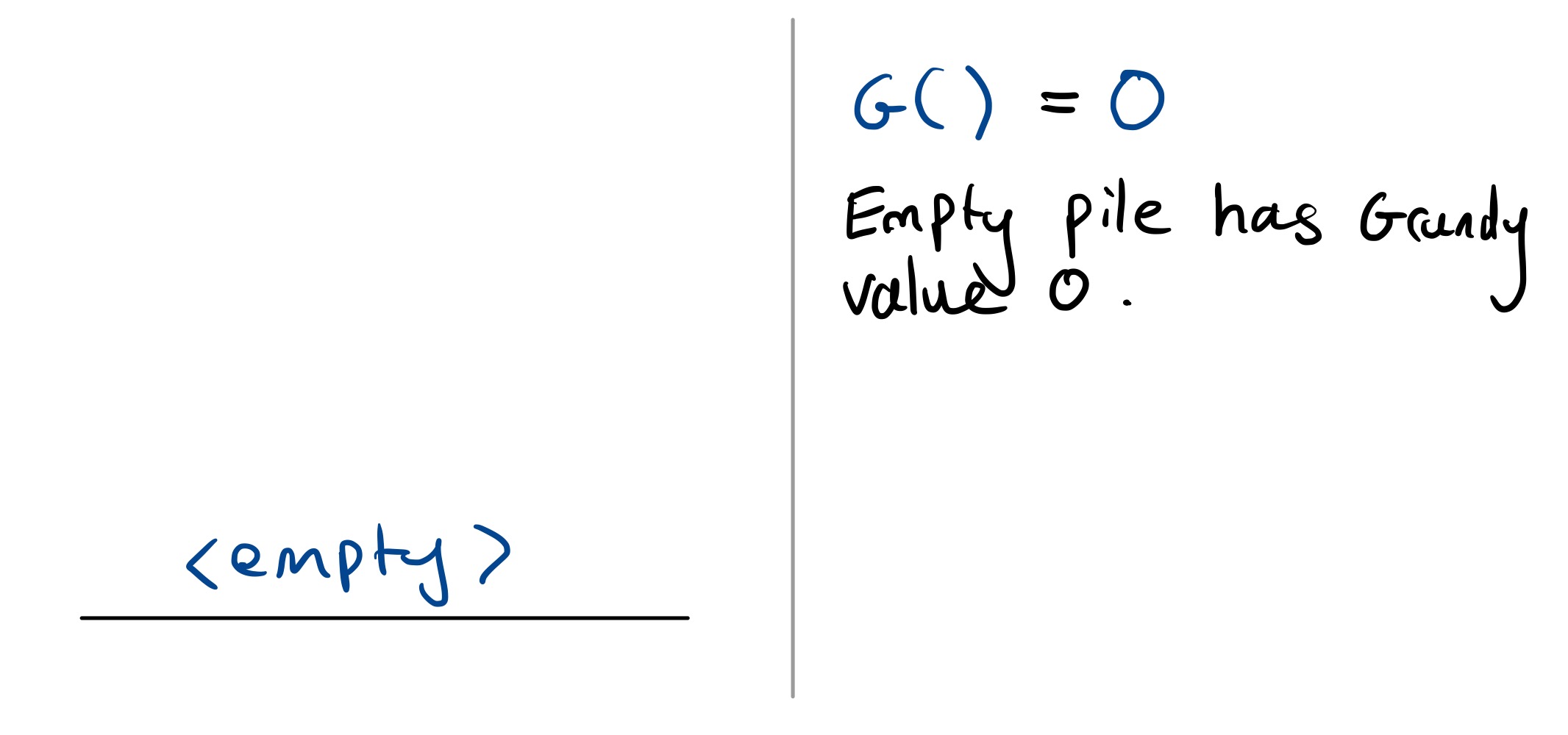
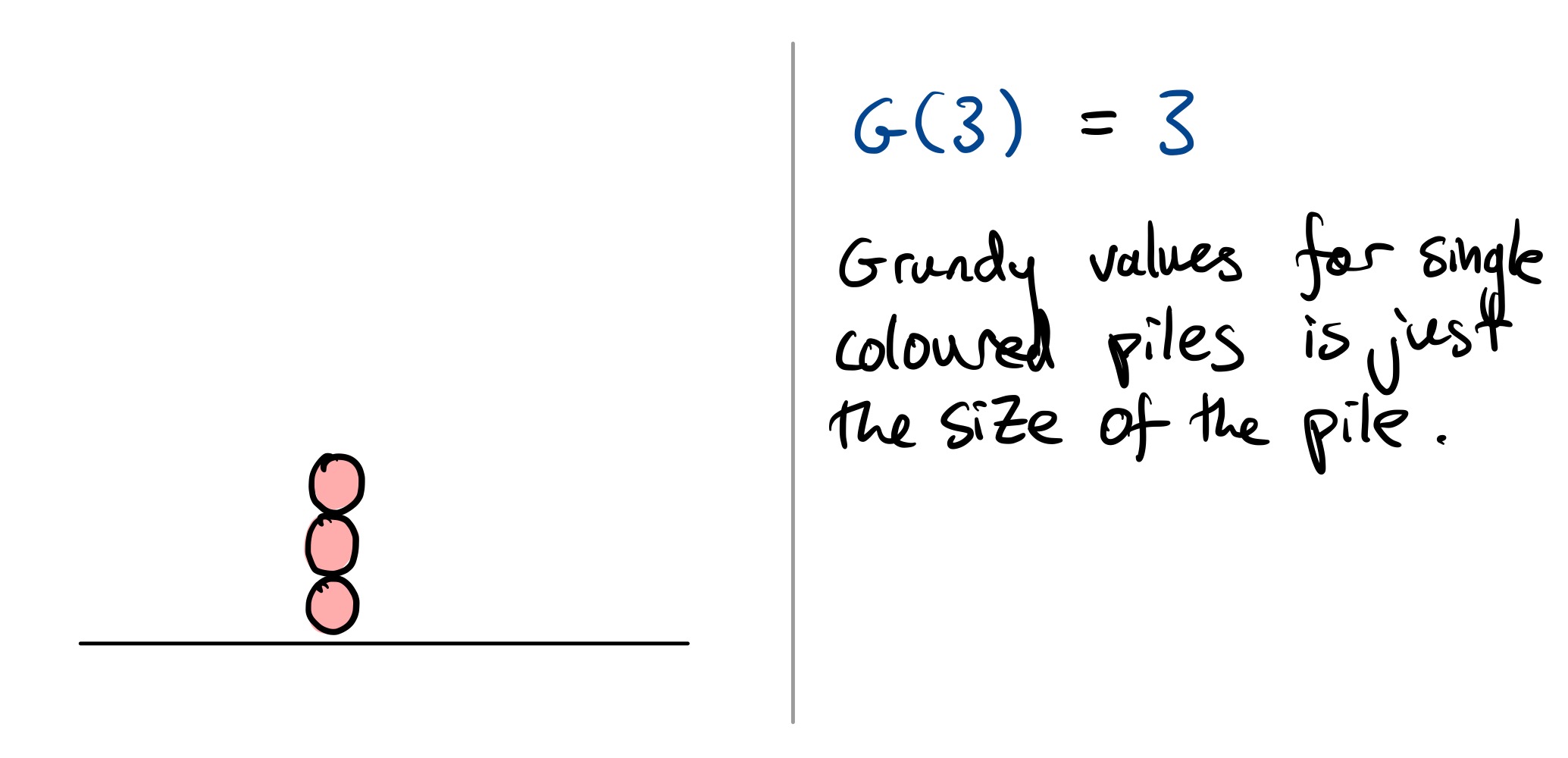
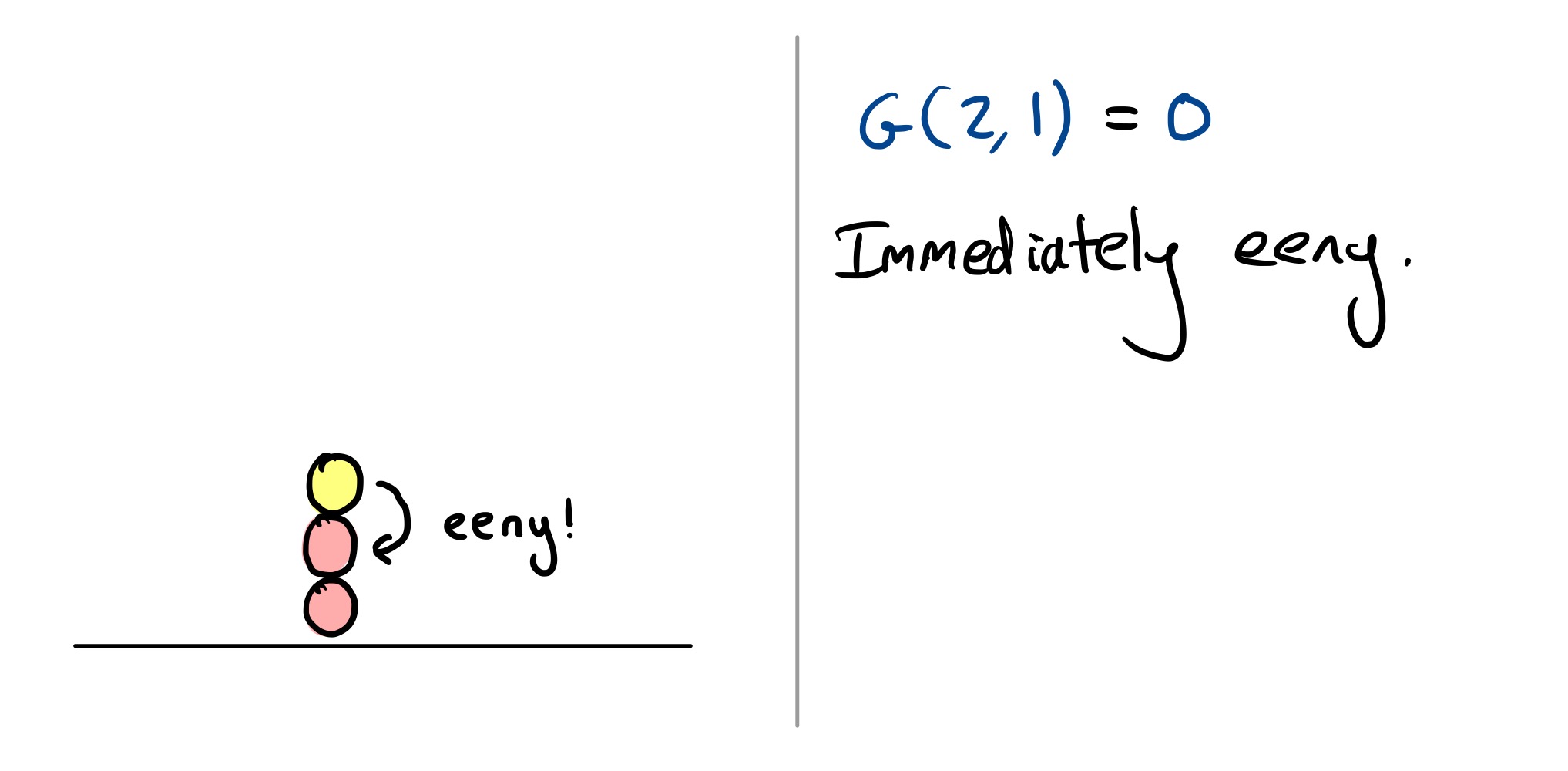

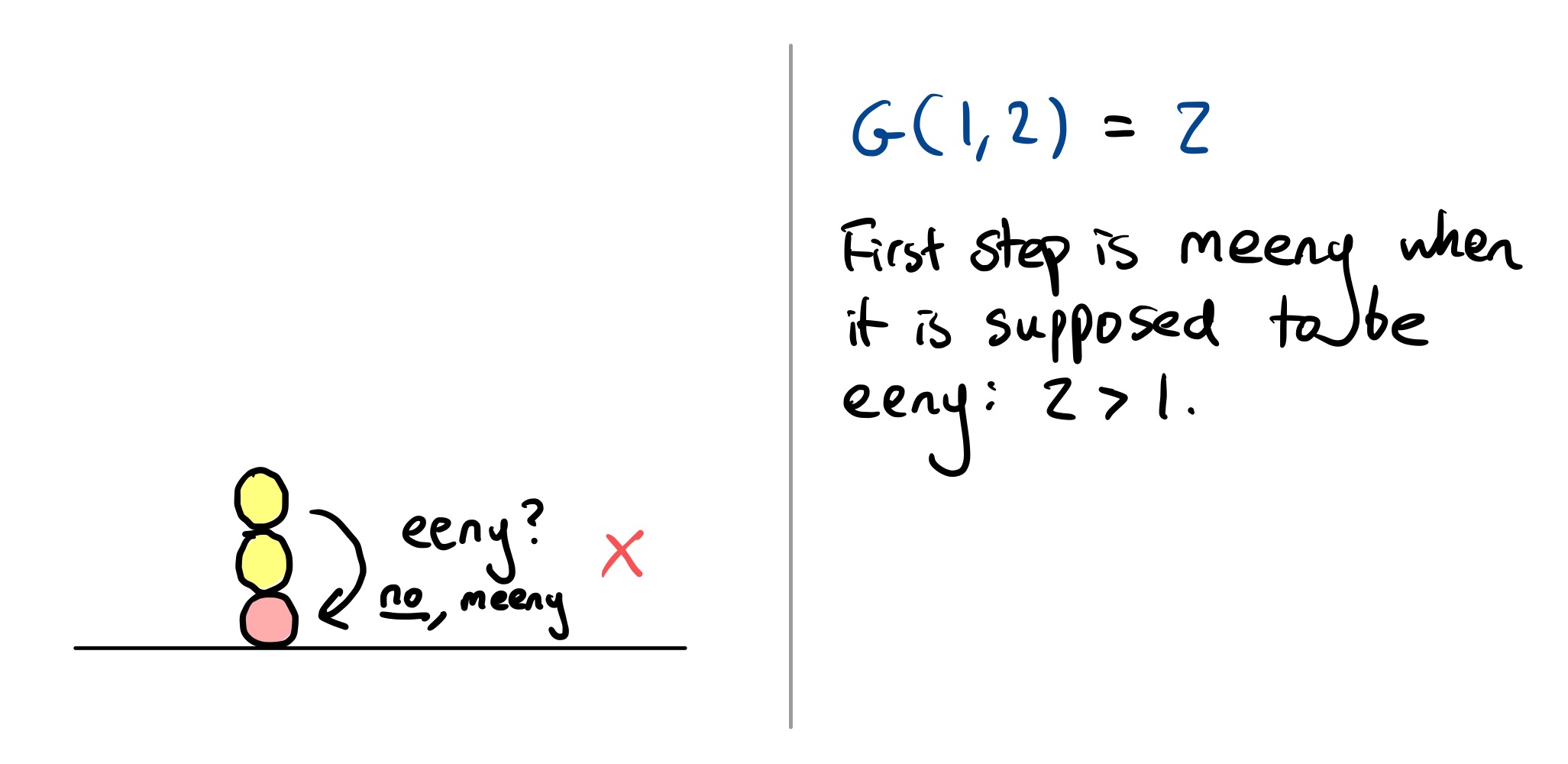
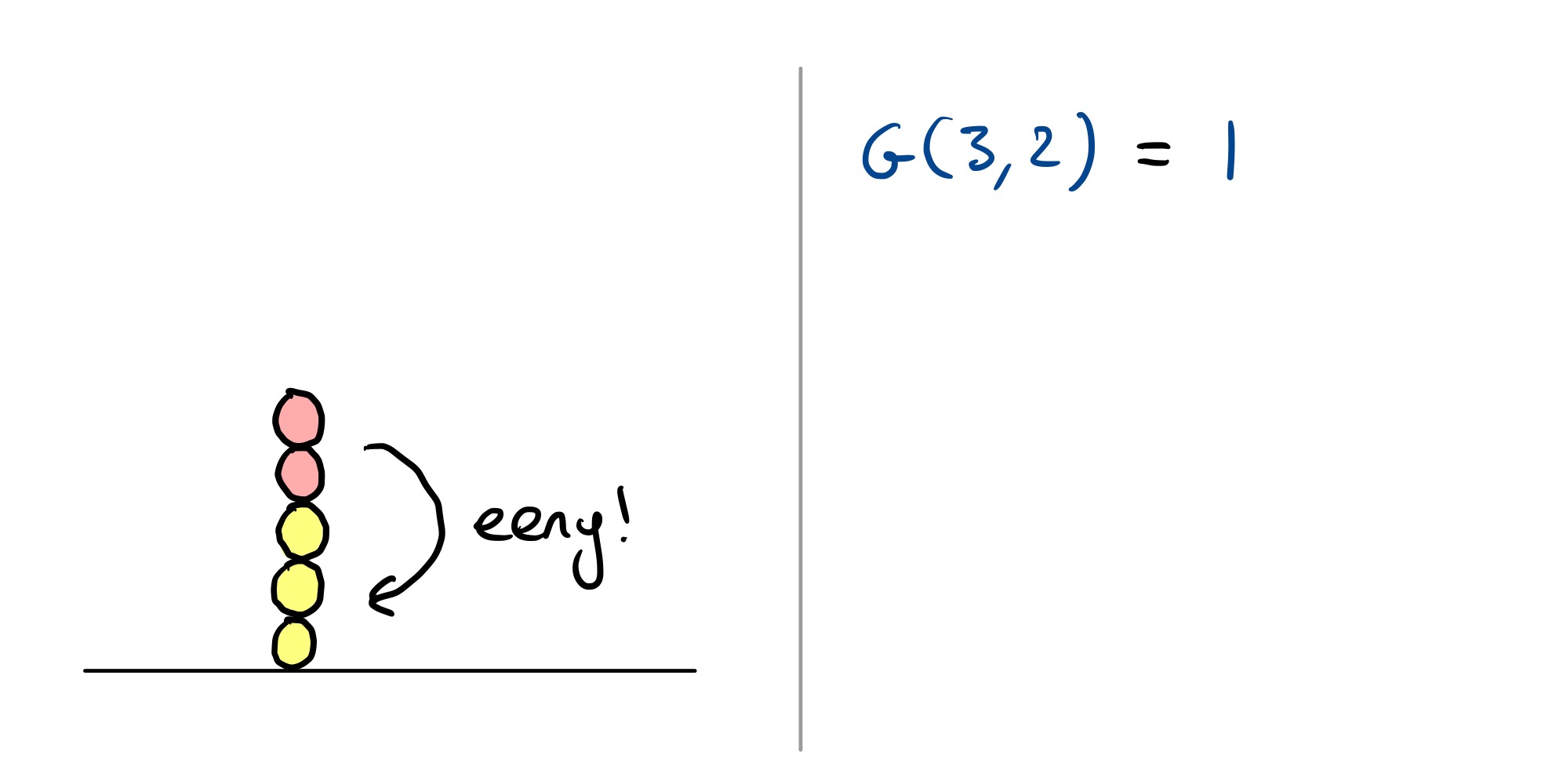
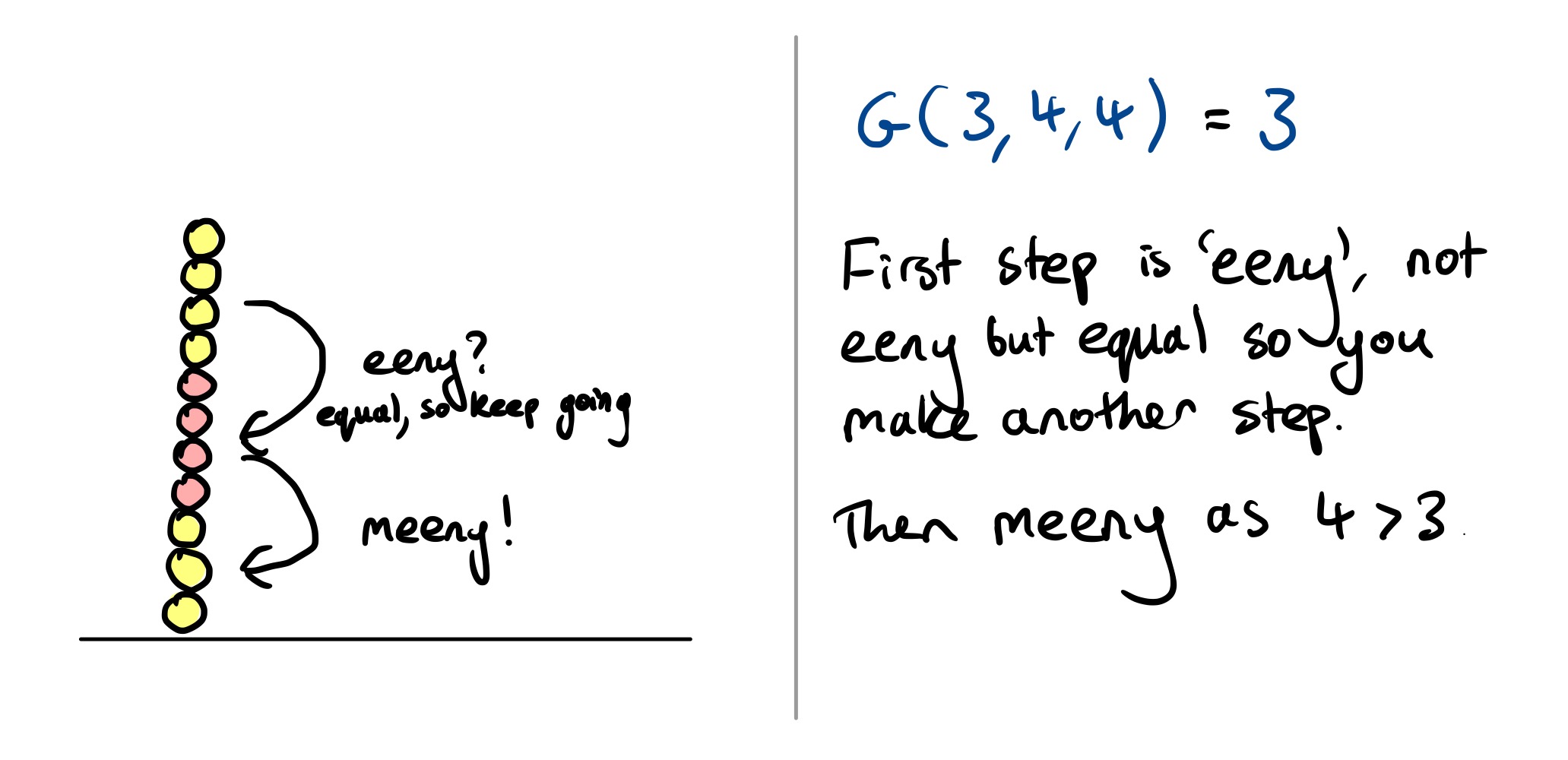




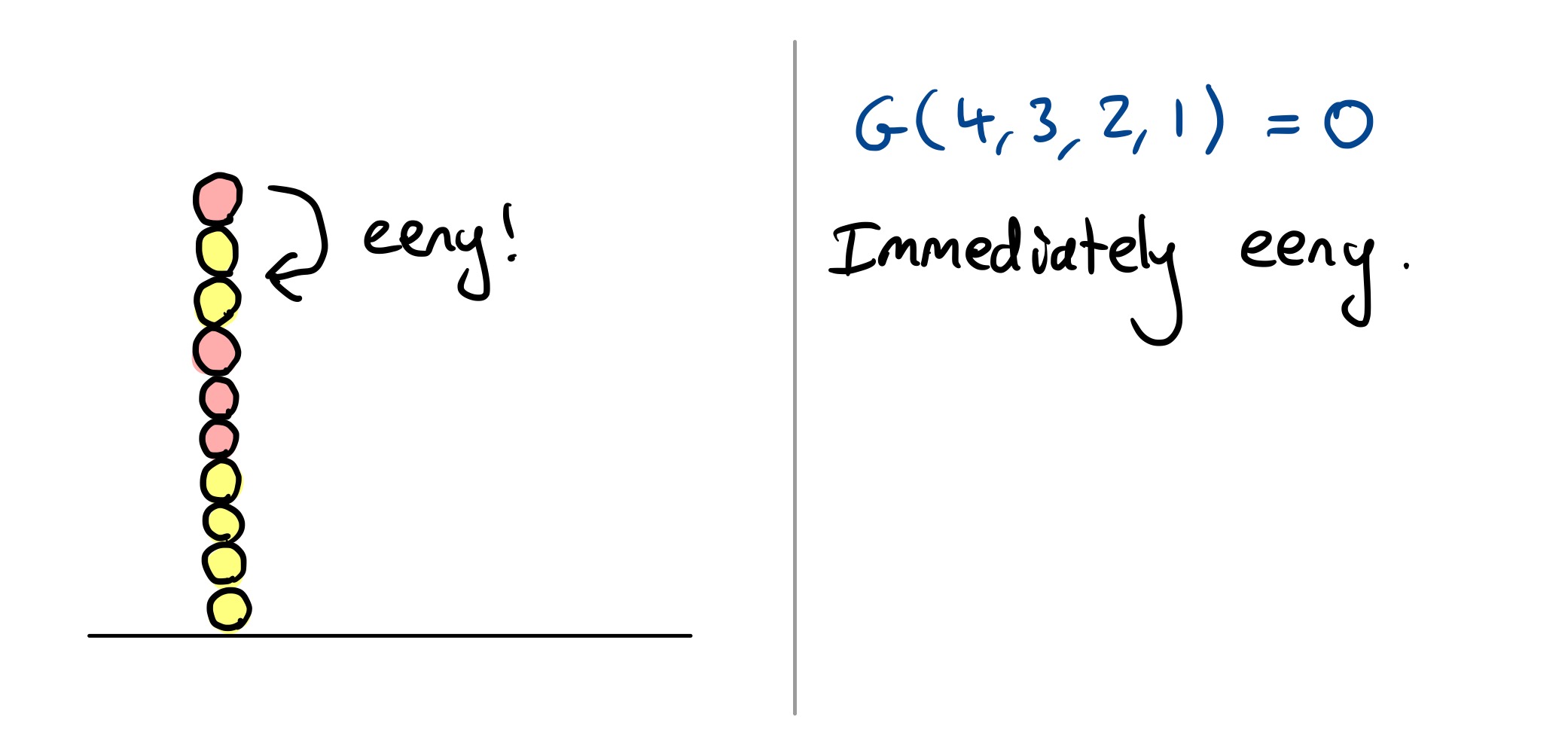
Winning (or losing)
After you’ve done this calculation for each pile, you’ll have a collection of Grundy values $g _ 1, \ldots, g _ m$ where $m$ is the number of piles. The best move to make is to make the bitwise XOR of all these values equal to zero, and in fact all other moves are losing.
More specifically, writing $g _ i \oplus g _ j$ for the bitwise XOR of two Grundy values $g _ i$ and $g _ j$, there are two cases:
- If you calculate $g _ 1 \oplus \cdots \oplus g _ m = 0$ at the start of your turn, then you are in trouble since if your opponent players perfectly, you have lost. In this case, your best bet is to move into the most complicated position you can spot, hoping they won’t be able analyse it.
- Otherwise, $g _ 1 \oplus \cdots \oplus g _ m \ne 0$. In this case, you can force a win. To do this, like in ordinary Nim, you should play a move that changes the bitwise XOR of all the piles to be zero.
Some example games
Game 1: A single pile
What’s the best move in this game with just a single pile?

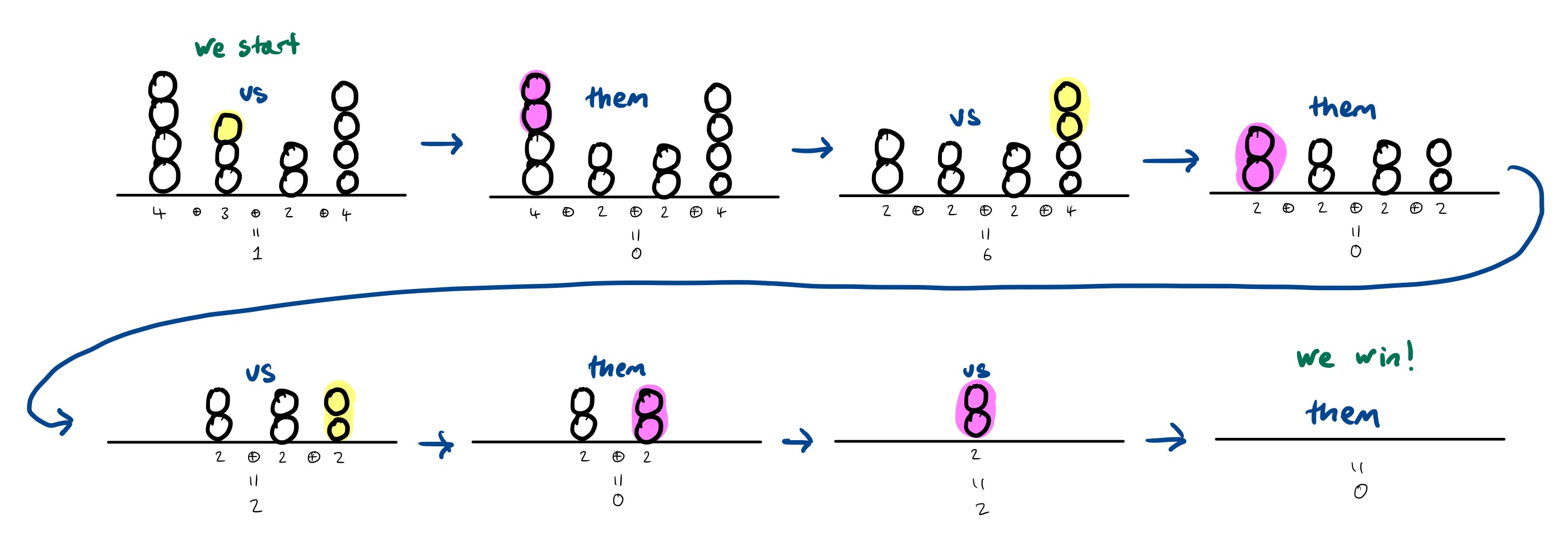
In the notation, this first position is $(1, 2, 2, 2)$. Here’s how you can win:
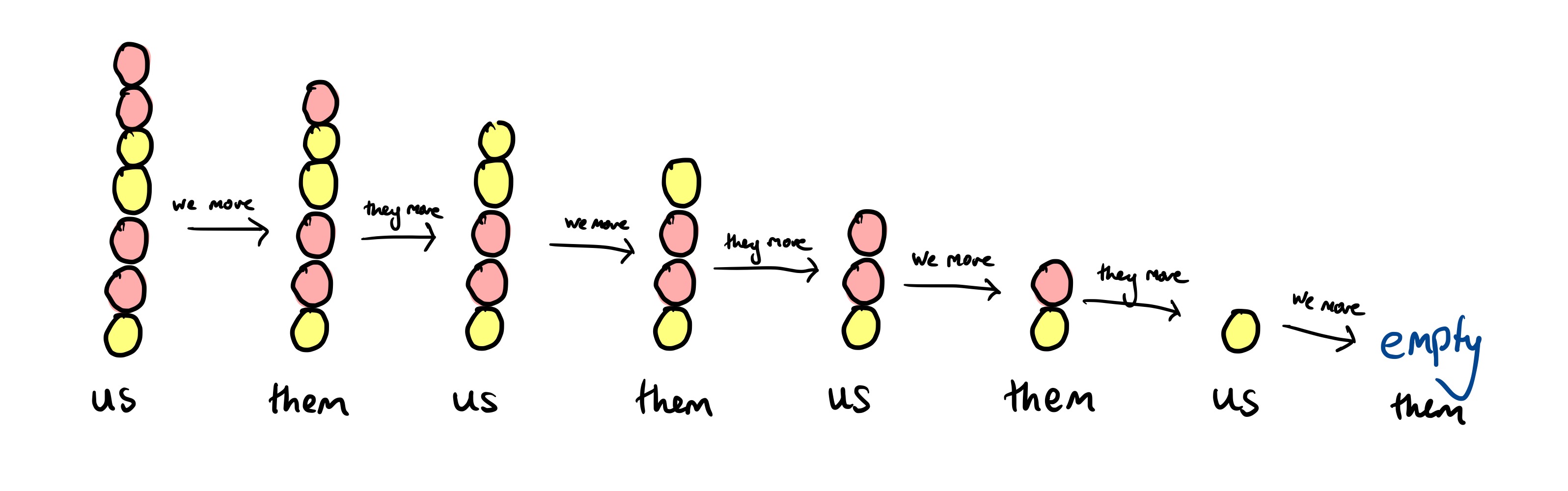
Or, annotated with the Grundy value of each intermediate pile:
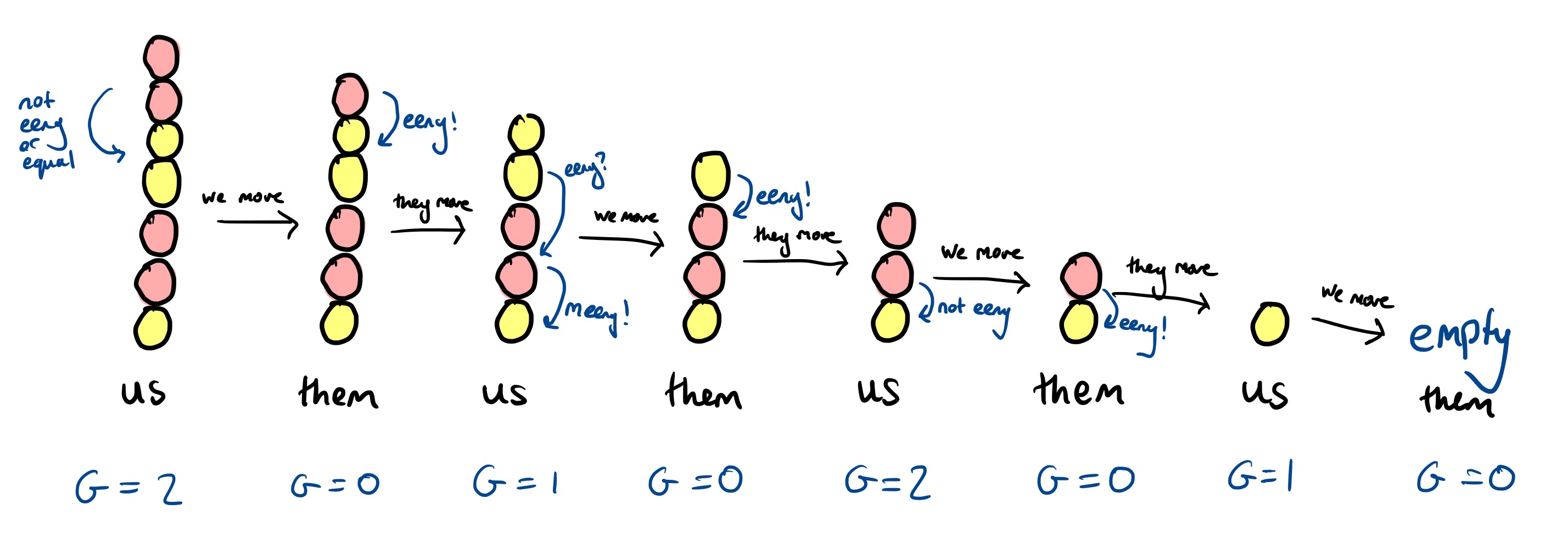
You don’t need the full complication of the eeny-meeny rule when there is just one pile, it’s reasonably easy to see which move wins. But it is vital when there is more than one pile.
Game 2: Two simple piles
What’s the move here?
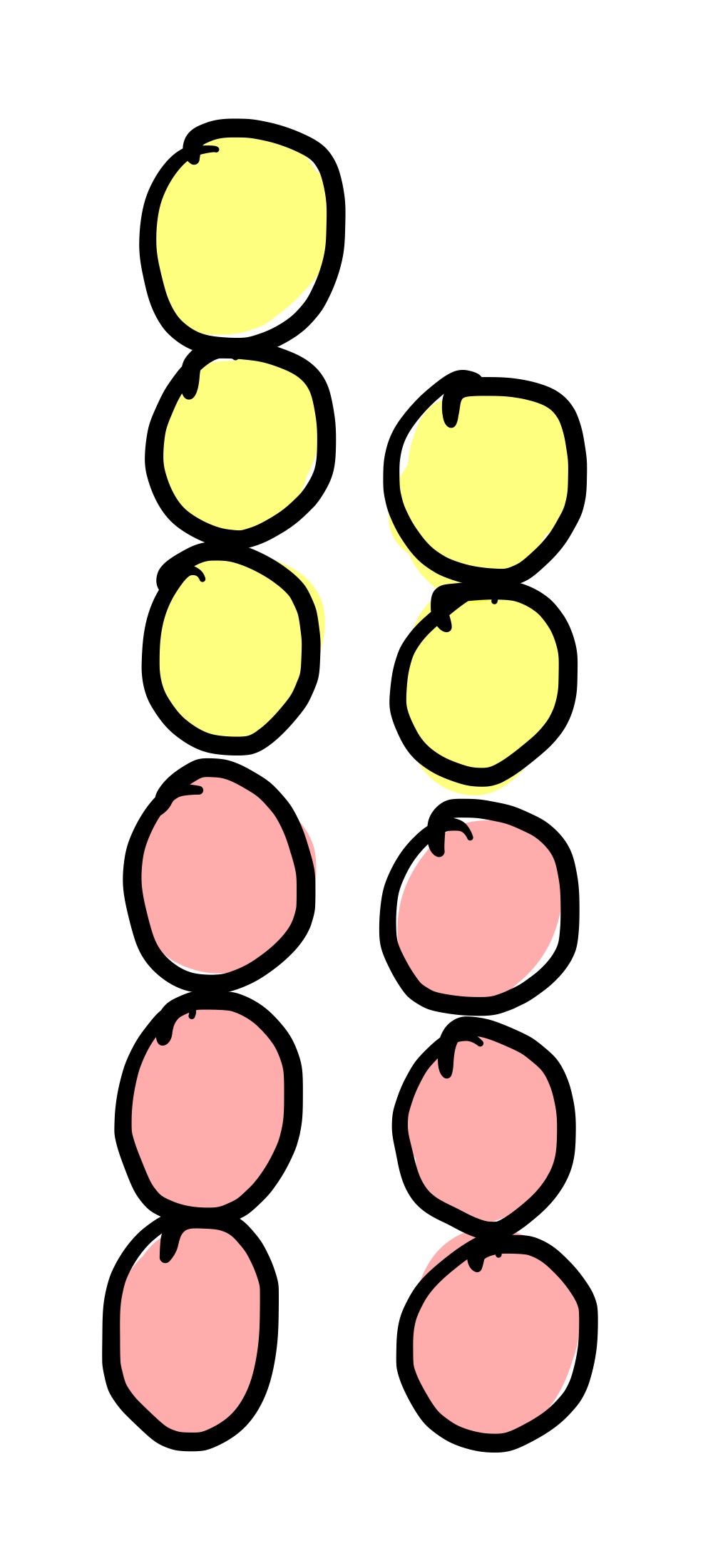
The Grundy value of the first pile is $2$, and the Grundy value of the second is $1$. To win, you therefore make the Grundy value of the first pile also $1$, since $1 \oplus 1 = 0$. To do this, remove just one ball from the first pile. Here’s an example game where you make that move:
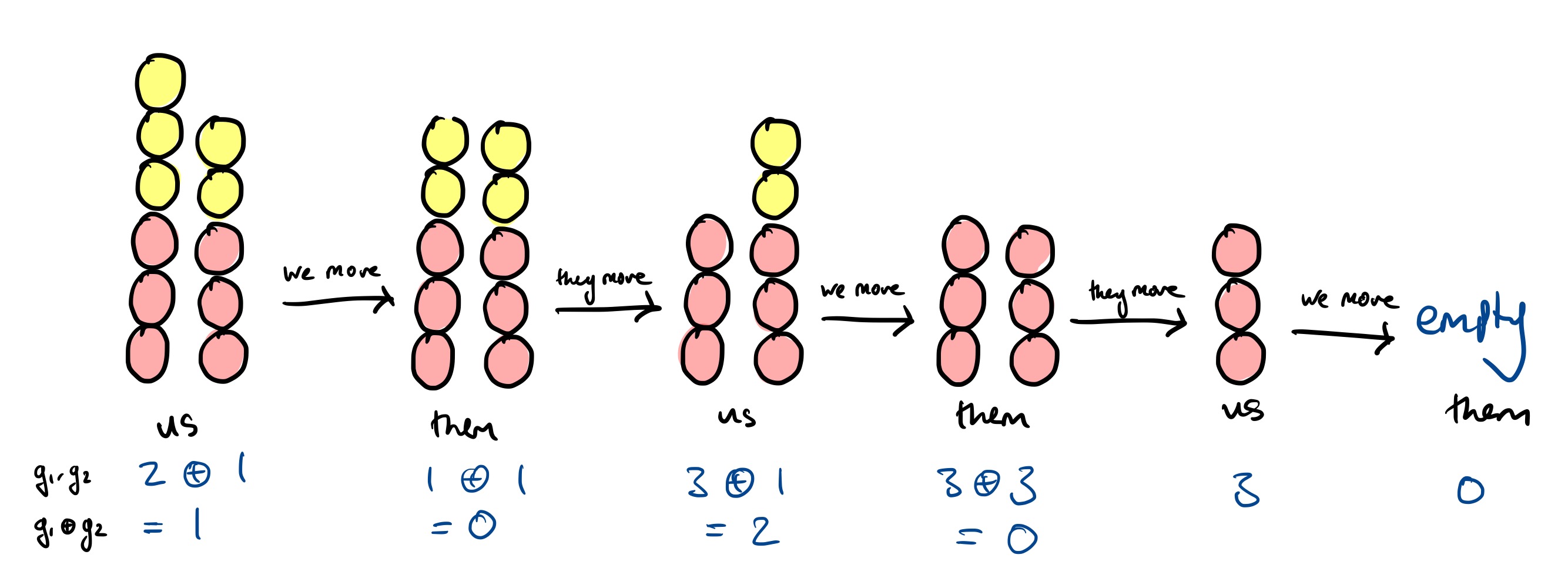
Game 3: Two complicated piles
Here’s a more complicated game, now the piles are unequal:
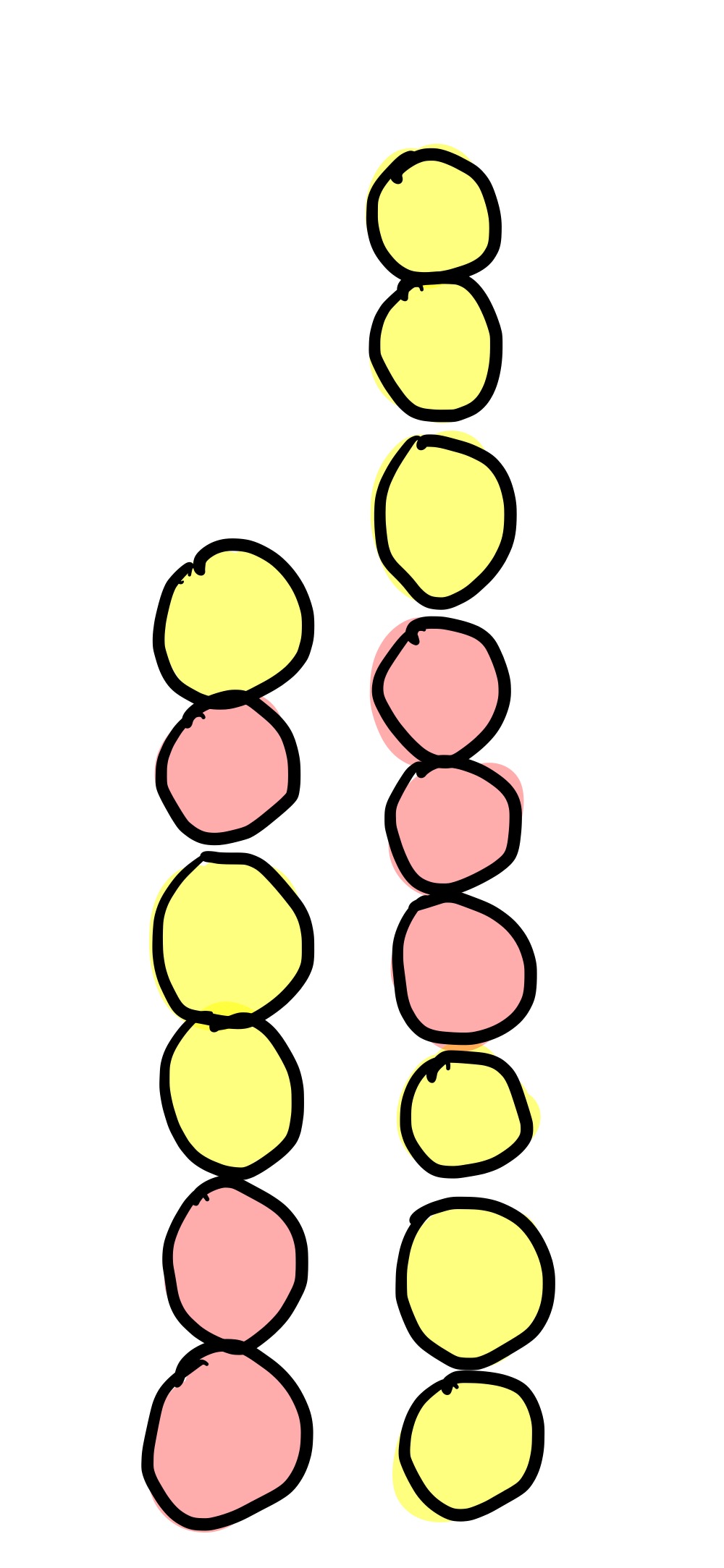
The move here is to take just one ball from the pile on the right. There’s lots of ways the game can unfold from this point, but you win in all of them. Here is one potential game:
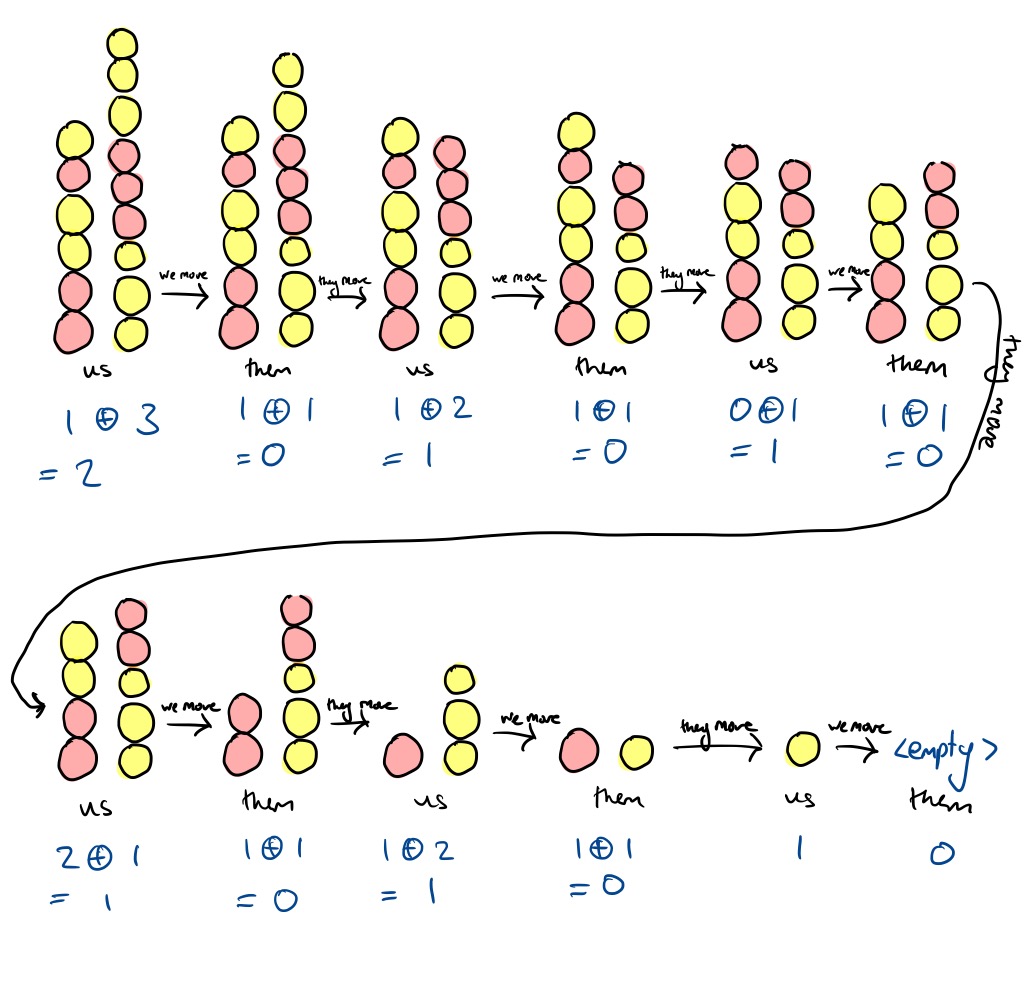
Game 4: Five complicated piles
How many winning moves are there in the following?
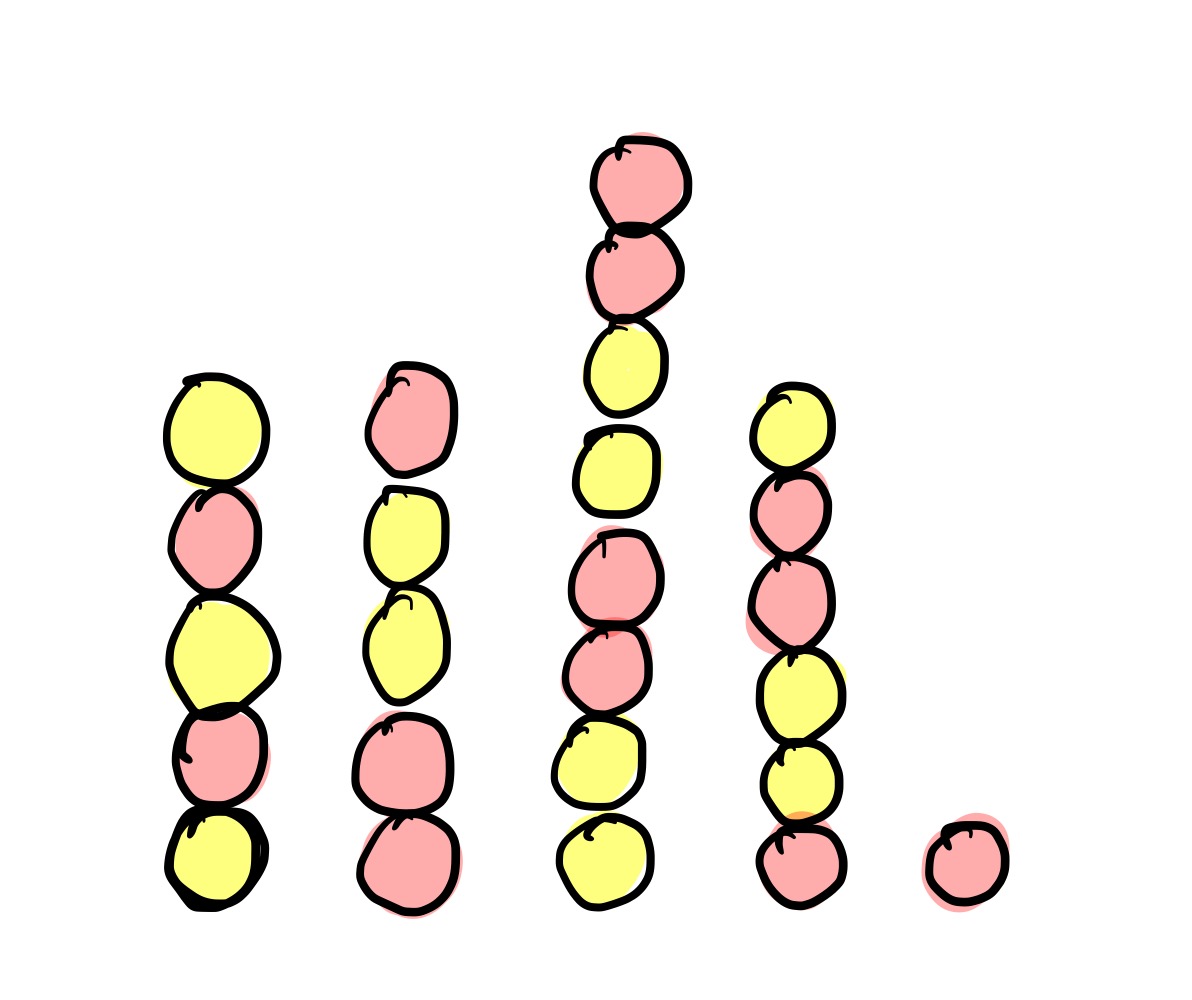
…there are in fact no winning moves. This is because the Grundy values are $1$, $0$, $1$, $1$ and $1$, and $1 \oplus 0 \oplus 1 \oplus 1 \oplus 1 = 0$.
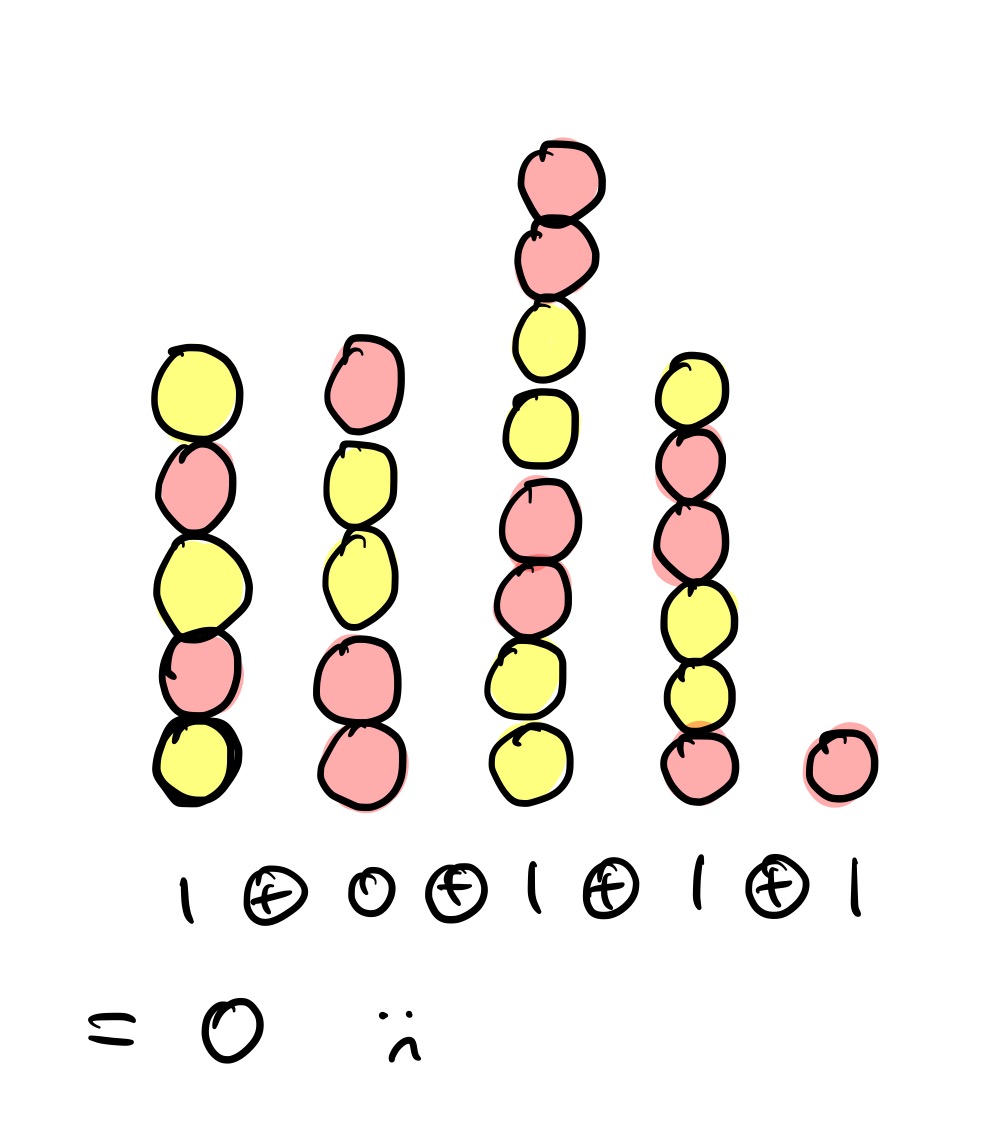
Any move you make will move to a position where the XOR is nonzero, and so if your opponent is using the eeny-meeny strategy, they will be able to win.
Some proofs and not-proofs of the eeny-meeny rule
This section is more technical and assumes some basic results and definitions in combinatorial game theory.
We defined a position as $(n _ 1, \ldots, n _ k)$. The possible moves from this position are to:
- $(n _ 1, \ldots, n _ {k-1})$, which corresponds to removing all balls in the top section
- For each $\ell < n _ k$, $(n _ 1, \ldots, n _ k - \ell)$, which corresponds to removing $\ell$ balls from the top section
For an arbitrary impartial game, the Grundy value of a position $\pmb p$ is defined as:
\[\begin{aligned} \mathcal G(\pmb p) &= \text{mex} \{\mathcal G(\pmb p') \mid \pmb p' \text{is reachable from }\pmb p\} \\\\ \mathcal G()&= 0 \end{aligned}\](here $\text{mex}$ is the minimum excludant, the smallest nonnegative natural number not appearing in the set). In our case, we have:
\[\mathcal G(n_1, \ldots, n_k) = \text{mex}(\{ \mathcal G(n_1, \ldots, n_{k-1}) \} \cup \{ \mathcal G(n_1, \ldots, n_k - \ell) \mid \ell < n_k\} \})\]From this it is clear that $\mathcal G(n _ 1) = n _ 1$, since by induction
\[\begin{aligned} \mathcal G(n_1) &= \text{mex}\{G(), G(1), \ldots, G(n_1 - 1)\} \\ &= \text{mex}\{0, 1, 2, \ldots, n_1-1\} \\ &= n_1 \end{aligned}\]Results from the theory of impartial games tells us that if we can calculate the Grundy value for each pile in colourful Nim, say $g _ 1, \ldots, g _ m$, then we can find the Grundy value of the overall game (where the possible moves are considered across every pile) by taking the bitwise XOR of each: $g _ 1 \oplus \cdots \oplus g _ n$. As a consequence of other results, making sure that $g _ 1 \oplus \ldots g _ n = 0$ at the end of your turn is enough to guarantee a win.
So justifying the eeny-meeny rule is the same as proving the following:
\[\text{mex}(\{ \mathcal G(n_1, \ldots, n_{k-1}) \} \cup \{ \mathcal G(n_1, \ldots, n_k - \ell) \mid \ell < n_k\} \}) = \begin{cases} n_{k} - 1 &\text{if eeny-meeny condition} \\ n_k &\text{otherwise} \end{cases}\]True for $k = 1$
The eeny-meeny rule says nothing about piles where $k = 1$, but it’s useful to record here what we already know:
\[\begin{aligned} \mathcal G(n_1) &= \text{mex}\{G(), G(1), \ldots, G(n_1 - 1)\} \\ &= \text{mex}\{0, 1, 2, \ldots, n_1-1\} \\ &= n_1 \end{aligned}\]True for $k = 2$
The eeny-meeny rule for $k = 2$ says that:
\[\mathcal G(n_1, n_2) = \begin{cases} n_2 - 1 &\text{if } n_2 \le n_1 \\ n_2 &\text{otherwise} \end{cases}\]We want to show that this is indeed equivalent to the actual definition:
\[\mathcal G(n_1, n_2) = \text{mex}(\{ \mathcal G(n_1) \} \cup \{ \mathcal G(n_1, n_2 - \ell) \mid \ell < n_k\} \})\]To do this, we can induct on $n _ 2$. The base case is $n _ 2 = 1$:
\[\begin{aligned} \mathcal G(n_1, 1) &= \text{mex}\{ \mathcal G(n_1) \} \\ &= \text{mex}\{n_1\} \\ &= \begin{cases} 0 &\text{if } n_1 \ne 0 \\ 1 &\text{otherwise} \end{cases} \\ &= \begin{cases} 0 &\text{if }1 \le n_1 \\ 1 &\text{otherwise} \end{cases} \end{aligned}\]which is indeed the eeny-meeny rule for $k = 2$.
Now consider $\mathcal G(n _ 1, n _ 2)$ where $n _ 2 > 1$. By strong induction, we can assume that for all $\mathcal G(n _ 1, n _ 2 - \ell)$, the eeny-meeny rule works, i.e.
\[\mathcal G(n_1, n_2 - \ell) = \begin{cases} n_2 - \ell -1 &\text{if }n_2-\ell \le n_1 \\ n_2-\ell &\text{otherwise} \end{cases}\]By the definition of $\mathcal G$, we have that:
\[\begin{aligned} \mathcal G(n_1, n_2) &= \text{mex}(\{ \mathcal G(n_1) \} \cup \{ \mathcal G(n_1, n_2 - \ell) \mid \ell < n_2\} \}) \\ &= \text{mex}(\{\mathcal G(n_1), \mathcal G(n_1, 1), \mathcal G(n_1, 2), \ldots, \mathcal G(n_1, n_2 - 1)\}) \\ &= \text{mex}(\{n_1, \mathcal G(n_1, 1), \mathcal G(n_1, 2), \ldots, \mathcal G(n_1, n_2 - 1)\}) \end{aligned}\]Now we consider cases.
Case 1: $n _ 2 \le n _ 1$. If this is true, then it must also be true that $n _ 2 - \ell \le n _ 1$ for all $\ell < n _ 2$. This means the eeny-meeny condition is satisfied for each $\mathcal G(n _ 1, n _ 2 - \ell)$, hence:
\[\begin{aligned} \mathcal G(n_1, n_2) &= \text{mex}(\{n_1, 0, 1, \ldots, n_2 - 2\}) \\ &= n_2 - 1 \end{aligned}\]So this case gives the eeny-meeny rule as we hope.
Case 2: $n _ 2 > n _ 1$. Then $n _ 1 = n _ 2 - m$ for some $m > 0$. Then:
\[\begin{aligned} G(n_1, n_2 - \ell) &= \begin{cases} n_2 - \ell -1 &\text{if }n_2-\ell \le n_1 \\ n_2 - \ell &\text{otherwise} \end{cases} \\ &= \begin{cases} n_2 - \ell - 1 &\text{if } \ell \ge m \\ n_2- \ell &\text{otherwise} \end{cases} \end{aligned}\]Plugging this into the definition for $\mathcal G(n _ 1, n _ 2)$, we have:
\[\begin{aligned} \mathcal G(n_1, n_2) &= \text{mex}(\{\mathcal G(n_1), \mathcal G(n_1, 1), \ldots, \mathcal G(n_1, n_2 - m), \mathcal G(n_1, n_2 - m + 1), \ldots, \mathcal G(n_1, n_2 - 1)\}) \\ &= \text{mex}(\{n_1, 0, \ldots, n_2 - m - 1, n_2 - m + 1, \ldots, n_2 - 1\}) \end{aligned}\]Since $n _ 1 = n _ 2 - m$, this means $\mathcal G(n _ 1, n _ 2) = n _ 2$ as we hope.
Combining the cases. Now this gives us a general formula for $\mathcal G(n _ 1, n _ 2)$:
\[\mathcal G(n_1, n_2) = \begin{cases} n_2 - 1 &\text{if } n_2 \le n_1 \\ n_2 &\text{otherwise} \end{cases}\]which is exactly the eeny-meeny rule for $k = 2$.
A useful result
If you squint, the proof for the $k = 2$ case can be adapted to show a stronger and more general result, namely that:
\[\begin{aligned} &(\star) & \mathcal G(n_1, \ldots, n_k) = \begin{cases} n_k - 1 &\text{if } n_k \le \mathcal G(n_1, \ldots, n_{k-1}) \\ n_k &\text{otherwise} \end{cases} \end{aligned}\]You can prove this more precisely by induction on $k$. The base cases are:
\[\begin{aligned} \mathcal G(n_1) &= n_1 \\ \mathcal G(n_1, n_2) &= \begin{cases} n_2 - 1 &\text{if } n_2 \le \mathcal G(n_1) \\ n_2 &\text{otherwise} \end{cases} \end{aligned}\]which is what we have just verified above.
Now consider $\mathcal G(n _ 1, \ldots, n _ k)$ where $k > 2$. By strong induction on $k$, we can assume that $(\star)$ holds for $\mathcal G(n _ 1, \ldots, n _ {k-1})$.
\[\mathcal G(n_1, \ldots, n_k) = \text{mex}(\{ \mathcal G(n_1, \ldots, n_{k-1}) \} \cup \{ \mathcal G(n_1, \ldots, n_k - \ell) \mid \ell < n_k\} \})\]We want to verify that $(\star)$ holds for this particular value of $k$. To do this, we now induct on $n _ k$, like how we inducted on $n _ 2$ for the $k = 2$ case.
Now inducting on $n _ k$, the base case we need to verify is that for $\mathcal G(n _ 1, \ldots, n _ {k-1}, 1)$:
\[\begin{aligned} \mathcal G(n_1, \ldots, n_{k-1}, 1) &= \text{mex}\{\mathcal G(n_1, \ldots, n_{k-1})\} \\ &= \begin{cases} 0 &\text{if } \mathcal G(n_1, \ldots, n_{k-1}) > 0 \\ 1 &\text{otherwise} \end{cases} \\ &= \begin{cases} 0 &\text{if } 1 \le \mathcal G(n_1, \ldots, n_{k-1}) \\ 1 &\text{otherwise} \end{cases} \\ \end{aligned}\]as required. So that establishes the base case for the induction on $n _ k$.
Now assume $n _ k > 1$. Like in the $k = 2$ case, we’ll break it down by cases again:
Case 1: $n _ k \le \mathcal G(n _ 1, \ldots, n _ {k-1})$. If this is true, then it must also be true that $n _ 2 - \ell \le \mathcal G(n _ 1, \ldots, n _ {k-1})$ for all $\ell < n _ k$, and so inductively :
\[\begin{aligned} \mathcal G(n_1, \ldots, n_k) &= \text{mex}(\{\mathcal G(n_1, \ldots, n_{k-1}), 0, 1, \ldots, n_k - 2\}) \\ &= n_k - 1 \end{aligned}\]So $(\star)$ is correct in this case.
Case 2: $n _ k > \mathcal G(n _ 1, \ldots, n _ {k-1})$. Then $G(n _ 1, \ldots, n _ {k-1}) = n _ k - m$ for some $m > 0$. Then:
\[\begin{aligned} G(n_1, \ldots, n_k - \ell) &= \begin{cases} n_k - \ell -1 &\text{if }n_k-\ell \le G(n_1, \ldots, n_{k-1}) \\ n_k - \ell &\text{otherwise} \end{cases} \\ &= \begin{cases} n_k - \ell - 1 &\text{if } \ell \ge m \\ n_k- \ell &\text{otherwise} \end{cases} \end{aligned}\]Plugging this into the definition for $\mathcal G(n _ 1, \ldots, n _ k)$, we have:
\[\begin{aligned} \mathcal G(n_1, \ldots, n_k) &= \text{mex}(\{\mathcal G(n_1, \ldots, n_{k-1}), \mathcal G(n_1, \ldots, n_{k-1}, 1), \ldots, \mathcal G(n_1, \ldots, n_{k-1}, n_{k} - m), \mathcal G(n_1, \ldots, n_{k-1}, n_k - m + 1), \ldots, \mathcal G(n_1, \ldots, n_{k-1}, n_k - 1)\}) \\ &= \text{mex}(\{\mathcal G(n_1, \ldots, n_{k-1}), 0, \ldots, n_k - m - 1, n_k - m + 1, \ldots, n_k - 1\}) \end{aligned}\]Since $\mathcal G(n _ 1, \ldots, n _ {k-1}) = n _ k - m$, this means $\mathcal G(n _ 1, \ldots, n _ k) = n _ k$ as we hope.
A breather
Here’s what we’ve shown so far: by definition, the Grundy value of a position is defined recursively by:
\[\begin{aligned} &G() = 0 \\ &\mathcal G(n_1, \ldots, n_k) = \text{mex}(\{ \mathcal G(n_1, \ldots, n_{k-1}) \} \cup \{ \mathcal G(n_1, \ldots, n_k - \ell) \mid \ell < n_k\} \}) \end{aligned}\]and as a base case.
We know now the following for certain:
\[\begin{aligned} &G(n_1) = n_1 \\ &\mathcal G(n_1, n_2) = \begin{cases} n_2 - 1 &\text{if } n_2 \le n_1 \\ n_2 &\text{otherwise} \end{cases} \end{aligned}\]and we have the more general formula:
\[\mathcal G(n_1, \ldots, n_k) = \begin{cases} n_k - 1 &\text{if } n_k \le \mathcal G(n_1, \ldots, n_{k-1}) \\ n_k &\text{otherwise} \end{cases}\]This is still a long way from proving the full eeny-meeny rule, which says that in general:
\[\mathcal{G}(n_1, \ldots, n_{2k}) = \begin{cases} n_{2k}-1 &\text{if }&& n_{2k} < n_{2k-1}, \text{ or} \\ & &&n_{2k} = n_{2k-1} > n_{2k-2}, \text{ or} \\ & && \quad\quad\quad\quad\quad\quad\vdots\\ & &&n_{2k} = n_{2k-1} = n_{2k-2} < n_{2k-3}, \text{or } \\ &\ldots\text{until}\ldots &&n_{2k} = n_{2k-1} = \cdots = n_2 > n_1 \\ \\ n_{2k} &\text{otherwise} && \end{cases}\]and
\[\mathcal{G}(n_1, \ldots, n_{2k-1}) = \begin{cases} n_{2k-1}-1 &\text{if }&& n_{2k} < n_{2k-1}, \text{ or} \\ & &&n_{2k} = n_{2k-1} > n_{2k-2}, \text{ or} \\ & && \quad\quad\quad\quad\quad\quad\vdots\\ & &&n_{2k} = n_{2k-1} = n_{2k-2} < n_{2k-3}, \text{or } \\ &\ldots\text{until}\ldots &&n_{2k} = n_{2k-1} = \cdots = n_2 \le n_1 \\ \\ n_{2k-1} &\text{otherwise} && \end{cases}\]In other words, the eeny-meeny rule gives a non-recursive formula for the Grundy value of an arbitrary position.
True for $k = 3$
We can use what we have shown so far to prove the eeny-meeny rule also works when $k = 3$, in other words justifying the correctness of the formula:
\[\mathcal G(n_1, n_2, n_3) = \begin{cases} n_3 - 1 &\text{if } &n_3 < n_2, \text{ or } \\ & & n_3 = n_2 > n_1 \\ n_3 &\text{otherwise} \end{cases}\]We know for sure that:
\[\mathcal G(n_1, n_2, n_3) = \begin{cases} n_3 - 1 &\text{if } n_3 \le \mathcal G(n_1, n_2) \\ n_3 &\text{otherwise} \end{cases}\]and that:
\[\mathcal G(n_1, n_2) = \begin{cases} n_2 - 1 &\text{if } n_2 \le n_1 \\ n_2 &\text{otherwise} \end{cases}\]Plugging the formula for $\mathcal G(n _ 1, n _ 2)$ into the above and considering all possible cases, we get:
\[\mathcal G(n_1, n_2, n_3) = \begin{cases} n_3 - 1 &\text{if } &n_3 \le \mathcal n_2 - 1 \text{ and } n_2 \le n_1,\text{ or} \\ & &n_3 \le n_2 \text{ and }n_2 > n_1 \\ n_3 &\text{otherwise} \end{cases}\]Simplifying slightly:
\[\mathcal G(n_1, n_2, n_3) = \begin{cases} n_3 - 1 &\text{if } &n_3 < n_2 \text{ and } n_2 \le n_1,\text{ or} \\ & &n_3 \le n_2 \text{ and }n_2 > n_1 \\ n_3 &\text{otherwise} \end{cases}\]So we have two conditions: one we know is the actual Grundy value, and the eeny-meeny condition. We want to show they are the same.
Write
\[\begin{aligned} &\pmb G = (n_3 < n_2 \text{ and } n_2 \le n_1) \text{ or } &\mathcal{(1)} \\ &\quad\quad\,(n_3 \le n_2 \text{ and } n_2 > n_1) &\mathcal{(2)}\\\\ &\pmb E = (n_3 < n_2) \text{ or } & \mathcal{(A)} \\ &\quad\quad\, (n_3 = n_2 \text{ and } n_2 > n_1) &\mathcal{(B)} \end{aligned}\]If we can show $\pmb G \iff \pmb E$, then we are done, since then the eeny-meeny rule corresponds to the true Grundy value.
Consider cases:
-
Case 1: $n _ 3 < n _ 2$:
- $\pmb E$ satisfied (by $\mathcal A$).
-
Case 1.1: $n _ 2 < n _ 1$:
- $\pmb G$ satisfied (by $\mathcal 1$).
-
Case 1.2: $n _ 2 = n _ 1$:
- $\pmb G$ satisfied (by $\mathcal 1$).
-
Case 1.3: $n _ 2 > n _ 1$:
- $\pmb G$ satisfied (by $\mathcal 2$).
-
Case 2: $n _ 3 = n _ 2$:
-
Case 2.1: $n _ 2 < n _ 1$:
- Neither $\pmb G$ or $\pmb E$ are satisfied.
-
Case 2.2: $n _ 2 = n _ 1$:
- Neither $\pmb G$ or $\pmb E$ are satisfied
-
Case 2.3: $n _ 2 > n _ 1$:
- Both $\pmb G$ and $\pmb E$ are satisfied (by $\mathcal 2$ and $\mathcal B$).
-
Case 2.1: $n _ 2 < n _ 1$:
-
Case 3: $n _ 3 > n _ 2$
- Neither $\pmb G$ or $\pmb E$ are satisfied.
Hence $\pmb G \iff \pmb E$, and so the eeny-meeny rule for $k = 3$ is correct.
True for $k = 4$
You can do the same thing for $k = 4$. We know that
\[\mathcal G(n_1, n_2, n_3, n_4) = \begin{cases} n_4 - 1 &\text{if } n_4 \le \mathcal G(n_1, n_2, n_3) \\ n_4 &\text{otherwise} \end{cases}\]and have just shown that
\[\mathcal G(n_1, n_2, n_3) = \begin{cases} n_3 - 1 &\text{if } &n_3 < n_2, \text{ or } \\ & & n_3 = n_2 > n_1 \\ n_3 &\text{otherwise} \end{cases}\]Substituting $\mathcal G(n _ 1, n _ 2, n _ 3)$ means you end up with
\[\mathcal G(n_1, n_2, n_3, n_4) = \begin{cases} n_4 - 1 &\text{if } \pmb G \\ n_4 &\text{otherwise} \end{cases}\]and you want to show that
\[\mathcal G(n_1, n_2, n_3, n_4) = \begin{cases} n_4 - 1 &\text{if } \pmb E \\ n_4 &\text{otherwise} \end{cases}\]is the same formula, where
\[\begin{aligned} &\pmb G = (n_4 < n_3 \text{ and } n_3 < n_2) \text{ or } &\mathcal{(1)} \\ &\quad\quad\, (n_4 < n_3 \text{ and } n_3 = n_2 \text{ and } n_2 > n_1) \text{ or } &\mathcal{(2)}\\ &\quad\quad\, (n_4 \le n_3 \text{ and } n_3 > n_2) \text{ or } &\mathcal{(3)} \\ &\quad\quad\,(n_4 \le n_3 \text{ and }n_3 \ge n_2 \text{ and } n_2 \le n_1) &\mathcal{(4)} \\\\ &\pmb E = (n_4 < n_3) \text{ or } &\mathcal{(A)} \\ &\quad\quad\,(n_4 = n_3 \text{ and } n_3 > n_2) \text{ or } &\mathcal{(B)} \\ &\quad\quad\,(n_4 = n_3 \text{ and } n_3 = n_2 \text{ and } n_2 \le n_1) &\mathcal{(C)}\\ \end{aligned}\]So again, the problem reduces to showing the equivalence between two sets of inequalities. Indeed, $E \iff G$:
-
Case 1: $n _ 4 < n _ 3$
- $\pmb E$ is satisfied (by $\mathcal A$).
-
Case 1.1: $n _ 3 < n _ 2$
- $\pmb G$ is satisfied (by $\mathcal 1$).
-
Case 1.2: $n _ 3 = n _ 2$
-
Case 1.2.1: $n _ 2 < n _ 1$
- $\pmb G$ is satisfied (by $\mathcal 4$).
-
Case 1.2.2: $n _ 2 = n _ 1$
- $\pmb G$ is satisfied (by $\mathcal 4$)
-
Case 1.2.3: $n _ 2 > n _ 1$
- $\pmb G$ is satisfied (by $\mathcal 2$).
-
Case 1.2.1: $n _ 2 < n _ 1$
-
Case 1.3: $n _ 3 > n _ 2$
- $\pmb G$ is satisfied (by $\mathcal 3$).
-
Case 2: $n _ 4 = n _ 3$
-
Case 2.1: $n _ 3 < n _ 2$
- Neither $\pmb G$ or $\pmb E$ are not satisfied.
-
Case 2.2: $n _ 3 = n _ 2$
-
Case 2.2.1: $n _ 2 < n _ 1$
- Both $\pmb G$ and $\pmb E$ are satisfied (by $\mathcal 4$ and $\mathcal C$)
-
Case 2.2.2: $n _ 2 = n _ 1$
- Both $\pmb G$ and $\pmb E$ are satisfied (by $\mathcal 4$ and $\mathcal C$)
-
Case 2.2.3: $n _ 2 > n _ 1$
- Neither $\pmb G$ or $\pmb E$ are satisfied.
-
Case 2.2.1: $n _ 2 < n _ 1$
-
Case 2.3: $n _ 3 > n _ 2$
- Both $\pmb G$ and $\pmb E$ are satisfied (by $\mathcal 3$ and $\mathcal B$)
-
Case 2.1: $n _ 3 < n _ 2$
-
Case 3: $n _ 4 > n _ 3$
- Neither $\pmb G$ or $\pmb E$ are satisfied.
So the eeny-meeny rule is the same as the actual Grundy value for $k = 4$.
True for $k > 4$?
As you can see, things get very hairy very quickly. You could apply the same technique for $k = 5$, but you would quickly end up in the dense mathematical thicket of cases, subcases, subsubcases and subsubsubcases. And worse, a manual proof like this is never going to be able to handle the general case for arbitrary $k$.
I can’t prove the general case, but have checked that the eeny-meeny rule works for 5, 6, and 7 colour changes where there are at most 6 balls in each section of colour, and would be very surprised if it fails to hold.
A general proof could look something like this: Induct on $k$, the number of colour changes. The base cases have already been proved above.
We want to show that:
\[\mathcal G(n_1, \ldots, n_k) = \begin{cases} n_k - 1 &\text{if the eeny-meeny condition is met} \\ n_k &\text{otherwise} \end{cases}\]More explicitly, this means showing that:
\[\mathcal{G}(n_1, \ldots, n_{2k}) = \begin{cases} n_{2k}-1 &\text{if }&& n_{2k} < n_{2k-1}, \text{ or} \\ & &&n_{2k} = n_{2k-1} > n_{2k-2}, \text{ or} \\ & && \quad\quad\quad\quad\quad\quad\vdots\\ & &&n_{2k} = n_{2k-1} = n_{2k-2} < n_{2k-3} \\ &\ldots\text{until}\ldots &&n_{2k} = n_{2k-1} = \cdots = n_2 > n_1 \\ \\ n_{2k} &\text{otherwise} && \end{cases}\]in the even case, and
\[\mathcal{G}(n_1, \ldots, n_{2k-1}) = \begin{cases} n_{2k-1}-1 &\text{if }&& n_{2k} < n_{2k-1}, \text{ or} \\ & &&n_{2k} = n_{2k-1} > n_{2k-2}, \text{ or} \\ & && \quad\quad\quad\quad\quad\quad\vdots\\ & &&n_{2k} = n_{2k-1} = n_{2k-2} < n_{2k-3} \\ &\ldots\text{until}\ldots &&n_{2k} = n_{2k-1} = \cdots = n_2 \le n_1 \\ \\ n_{2k-1} &\text{otherwise} && \end{cases}\]in the odd case.
Start with the even case. By one of the results above, we have:
\[\mathcal G(n_1, \ldots, n_{2k}) = \begin{cases} n_{2k} - 1 &\text{if } n_{2k} \le \mathcal G(n_1, \ldots, n_{2k-1}) \\ n_{2k} &\text{otherwise} \end{cases}\]You’d then need to apply the inductive hypothesis and substitute $\mathcal{G}(n _ 1, \ldots, n _ {2k-1})$ with the general eeny-meeny rule for odd-sized piles. If, after simplifying, you end up with the eeny-meeny rule for even-sized piles you would’ve proved the even case.
Then move onto the odd case. Again, we have:
\[\mathcal G(n_1, \ldots, n_{2k-1}) = \begin{cases} n_{2k-1} - 1 &\text{if } n_{2k-1} \le \mathcal G(n_1, \ldots, n_{2k-2}) \\ n_{2k-1} &\text{otherwise} \end{cases}\]You’d then need to apply the inductive hypothesis again and substitute $\mathcal{G}(n _ 1, \ldots, n _ {2k-2})$ with the general eeny-meeny rule for even-sized piles. Again, if you then end up with the eeny-meeny rule for odd-sized piles, you would’ve proved the odd case.
And if you’ve proved these two cases, you’ve proved the eeny-meeny works in general.
Further generalisations
Colourful Nim is a generalisation of ordinary Nim – ordinary Nim is just the special case where there are no colour changes. But what are some ways you could generalise further?
3-colour Nim?
What about instead of having two colours, you have three?
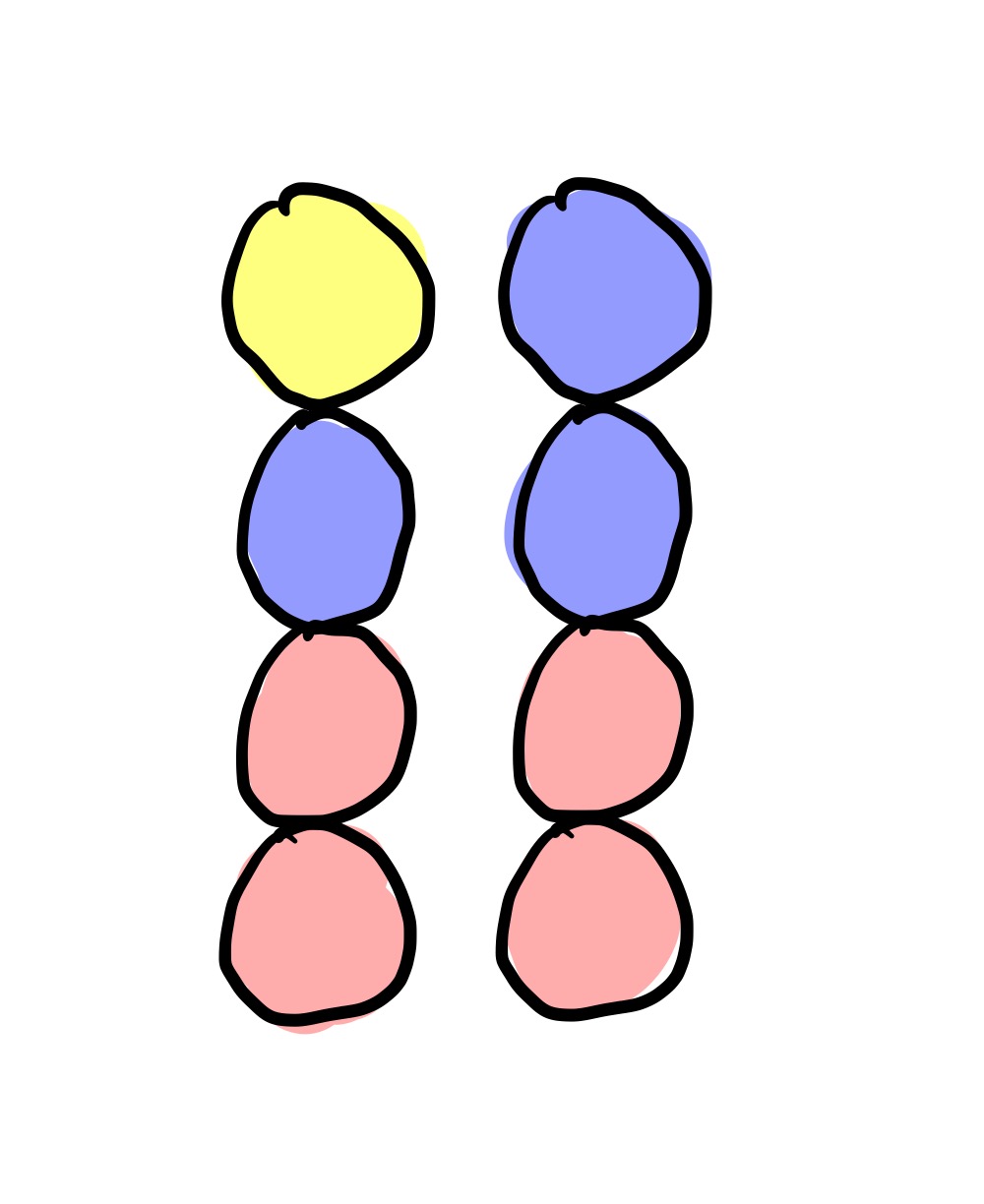
Unfortunately, this is no more interesting or difficult than having 2 colours like above. The reason for this is that the colours don’t actually matter, only the colour changes. So the above game is equivalent to the 2-colour game:
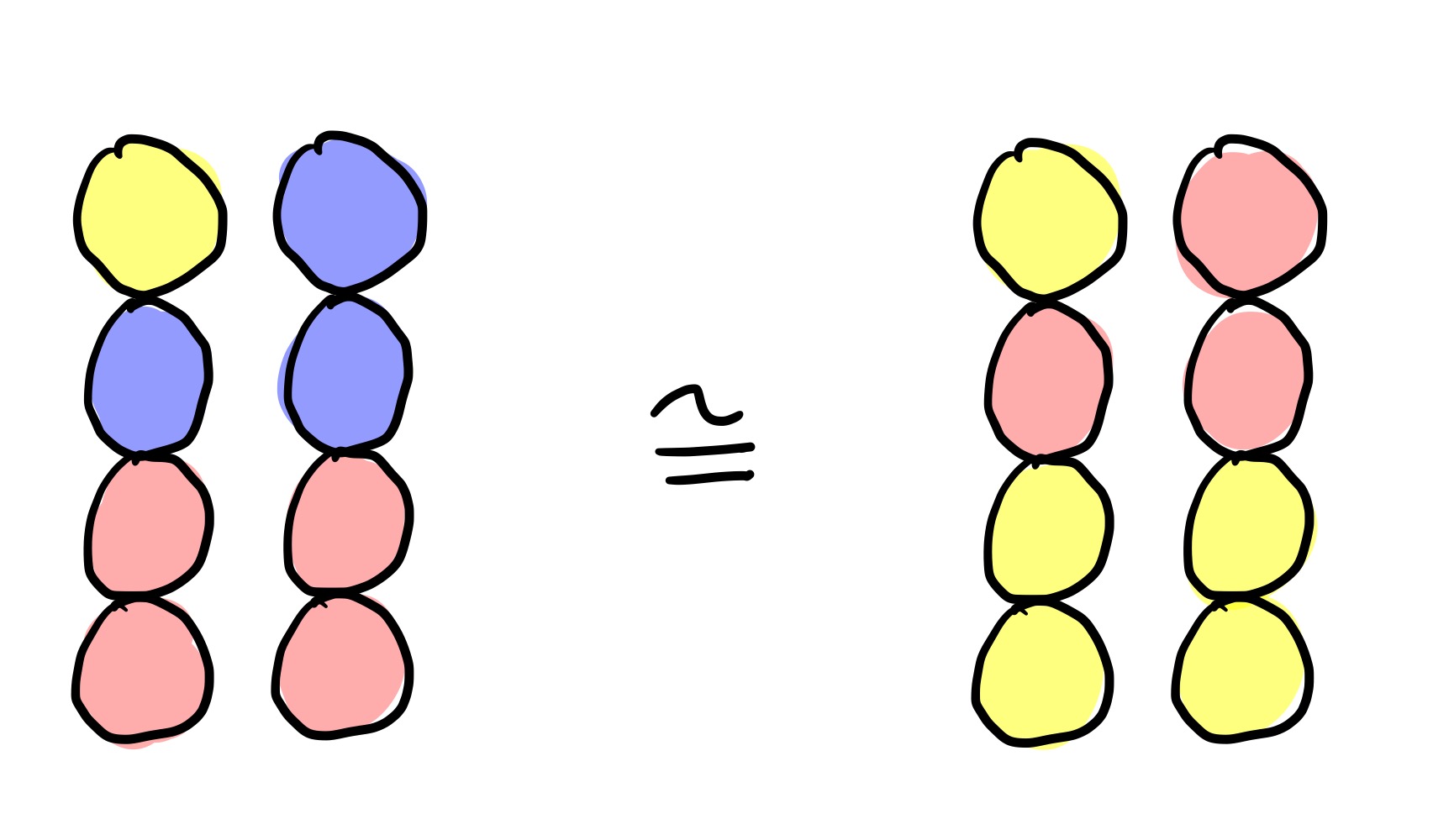
So to play 3-colour Nim, just translate it into 2-colour Nim and play with the eeny-meeny rule like above.
Taking balls from both ends
What about if you can take balls from both ends of each pile?
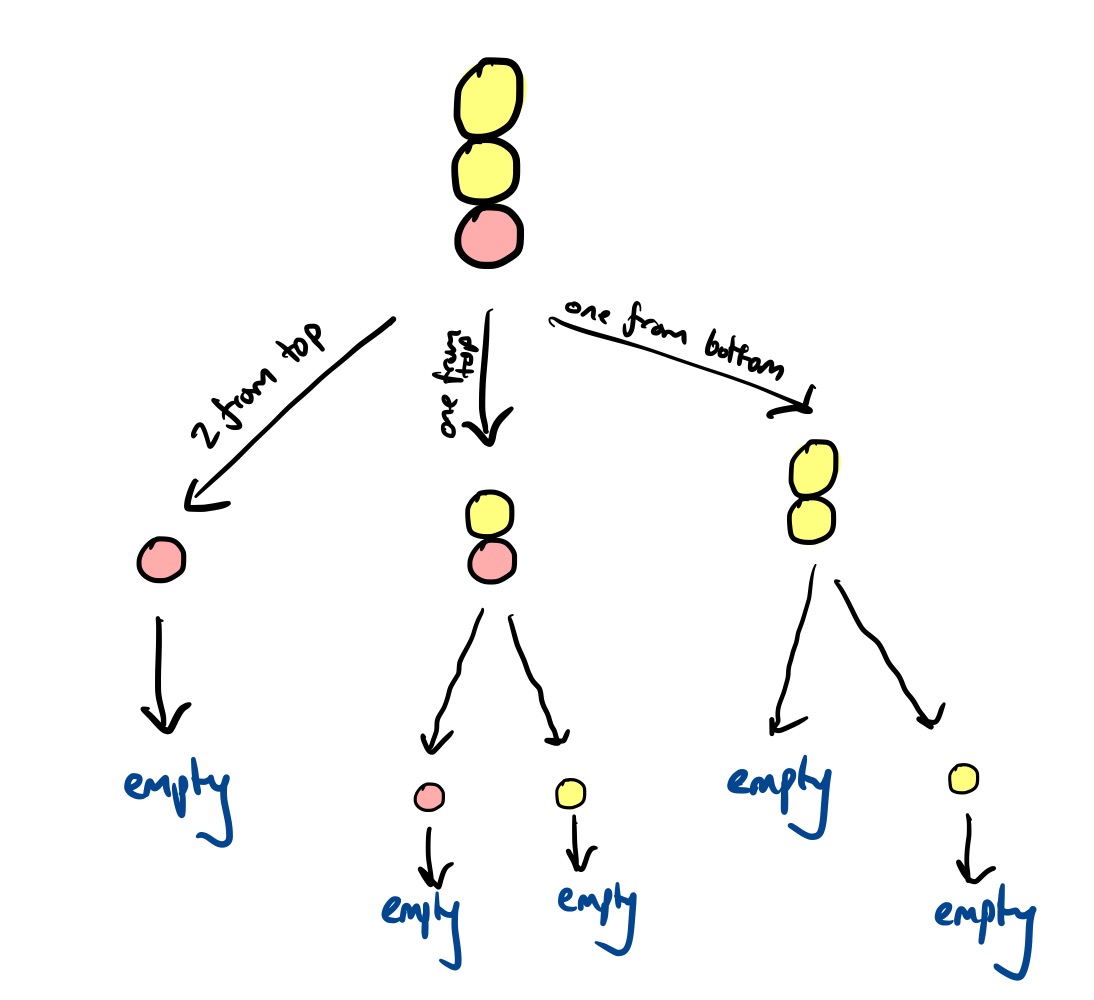
This a bit more complicated. The general strategy would still stand, namely calculating the Grundy value of each pile and then making the XOR equal to zero. But the problem once again becomes how to efficiently calculate the Grundy value.
Here are the Grundy values (calculated by a computer) of all piles with three colour changes and with at most three balls per section:
| (n1, n2, n3) | G(n1, n2, n3) |
|---|---|
| $(1,1,1)$ | $1$ |
| $(2,1,1)$ | $2$ |
| $(3,1,1)$ | $3$ |
| $(1,2,1)$ | $0$ |
| $(2,2,1)$ | $1$ |
| $(3,2,1)$ | $2$ |
| $(1,3,1)$ | $0$ |
| $(2,3,1)$ | $3$ |
| $(3,3,1)$ | $1$ |
| $(1,1,2)$ | $2$ |
| $(2,1,2)$ | $0$ |
| $(3,1,2)$ | $1$ |
| $(1,2,2)$ | $1$ |
| $(2,2,2)$ | $2$ |
| $(3,2,2)$ | $3$ |
| $(1,3,2)$ | $3$ |
| $(2,3,2)$ | $0$ |
| $(3,3,2)$ | $2$ |
| $(1,1,3)$ | $3$ |
| $(2,1,3)$ | $1$ |
| $(3,1,3)$ | $0$ |
| $(1,2,3)$ | $2$ |
| $(2,2,3)$ | $3$ |
| $(3,2,3)$ | $0$ |
| $(1,3,3)$ | $1$ |
| $(2,3,3)$ | $2$ |
| $(3,3,3)$ | $3$ |
(Here’s a longer list of calculations for bigger positions, and some more results are collected in [[Double-ended colourful Nim]]N).
Sequences of impartial games in general
A one-pile colourful Nim game could also be seen as a sequence of one-pile Nim games, where the loser of each sub-game goes first in the next-sub game.
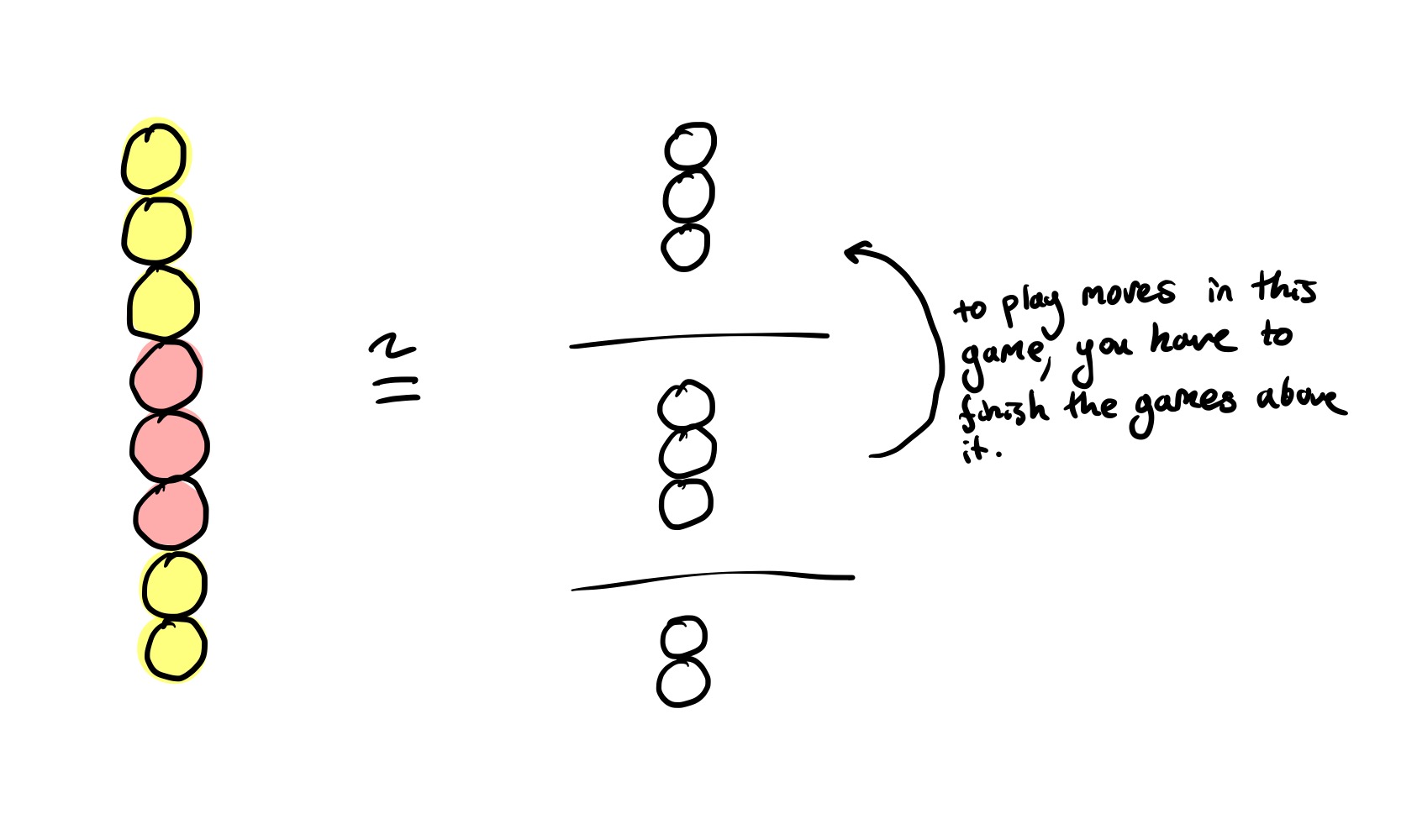
But what if you make each game in the sequence more complicated? For example, you could instead play a sequence of three multiple-pile Nim games:
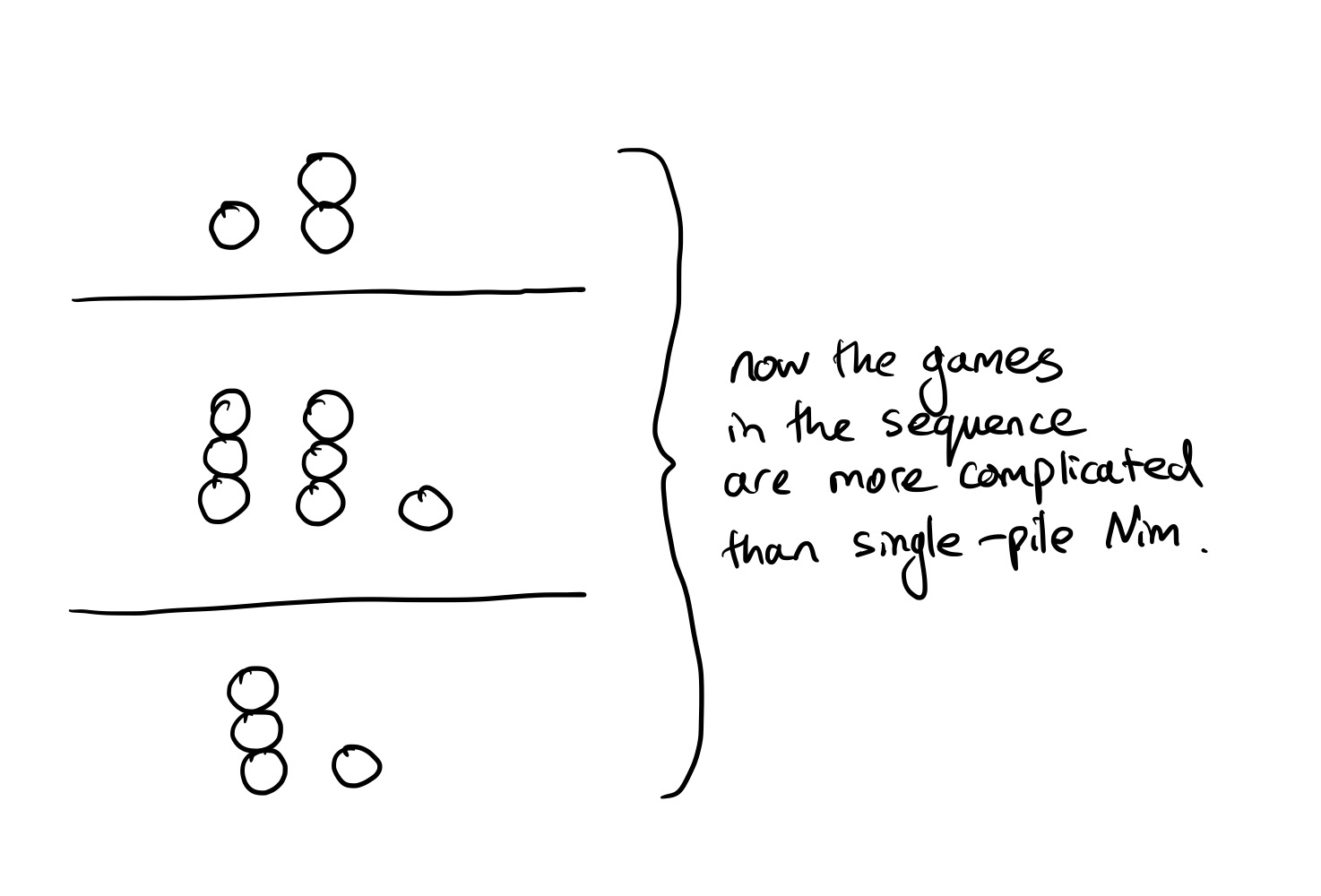
This is also much more complicated. One thing that definitely won’t work is calculating the Grundy value of each game in the sequence, and then considering the corresponding colourful Nim game, like so:
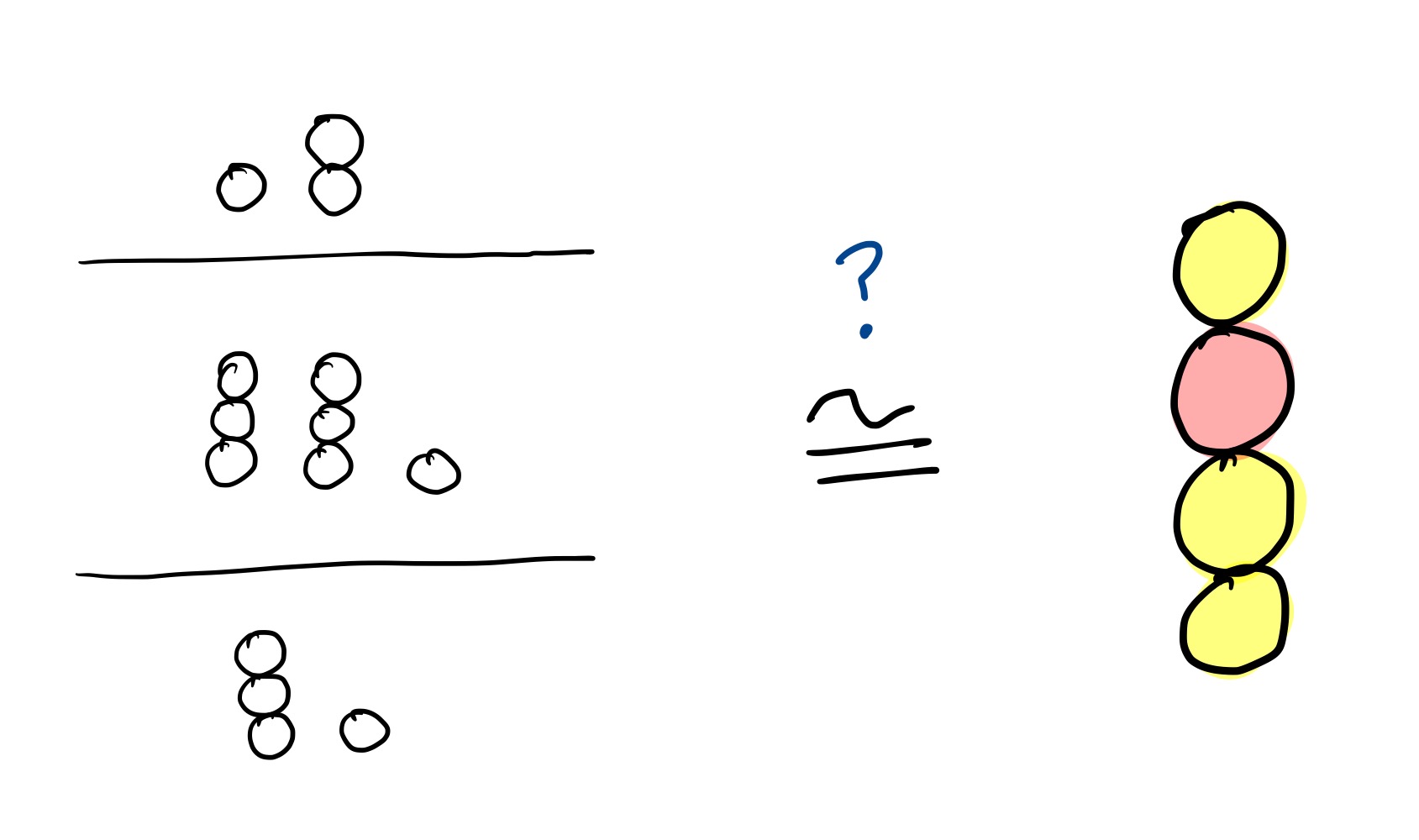
It’s a reasonable guess that you can just omit these zero games and “compress” the stack before applying the rule, but this is not the case – consider the game $(1, [2,2])$ where $[2, 2]$ denotes a game with two Nim piles of two stones each. Since $[2, 2]$ has Grundy value $0$ by the XOR trick, this guess would say that the overall Grundy value is $1$, and hence winnable for us. But by trying to win this game yourself, you can see that this is impossible.
But it gets worse – the Grundy value of the overall game cannot be any function of the Grundy values of each intermediate game. To see this, consider this game:
\[([n _ 1^{(1)}, \ldots, n _ {k _ 1}^{ {(1)} }], [n _ 1^{(2)}, \ldots, n _ {k _ 2}^{ {(2)} }], \ldots, [n _ 1^{(\ell)}, \ldots, n _ {k _ \ell}^{ { (\ell) } }])\](i.e. a sequence of $\ell$ games of Nim, at the top a $k _ \ell$ pile Nim game, followed by a $k _ {\ell - 1}$ pile game, and so on, until a $k _ 1$ pile game).
The Grundy value of this game cannot be a function of the Grundy values of the intermediate games, i.e.
\[\mathcal G([n_1^{(1)}, \ldots, n_{k_1}^{ {(1)} }], \ldots, [n_1^{(\ell)}, \ldots, n_{k_\ell}^{ {(\ell)} }]) \ne f(n_1^{(1)} \oplus \cdots \oplus n_{k_1}^{ {(1)} }, \ldots, n_1^{(\ell)} \oplus \cdots \oplus n_{k_\ell}^{ {(\ell)} }])\]for any $f$. If this were the case, $([1], [1,1])$ and $([1], [2,2])$ would have the same Grundy value, but this can’t be the case since $([1], [1,1])$ is a win for the first player, while $([1], [2,2])$ is a loss.
This means, among other things, that it’s not possible to come up with a uniform strategy for all sequences of impartial games just by considering the Grundy values of each impartial game in the sequence, and converting it to a game of Nim.
Another reason to expect that it is much more complicated is because a general strategy for playing sequences of games where you have the perfect strategies for the intermediate games would give you a general technique for misère play of any impartial game. The misère version of an impartial game is where you change the win condition so that whoever makes the last move loses.
Misère play is surprisingly often much more complicated than normal play – here’s the winning strategy for misère Nim, paraphrasing from [[On Numbers and Games, Conway]]N:
“Play as you would in normal Nim, making the XOR of the heap-sizes zero, unless your move would leave only heaps of size one, (discounting empty heaps). In this case, move so as to leave either one more or one fewer one-heaps than the normal play move.”
If you had a general rule for playing sequences of impartial games, you could convert any game into its misère variant by considering the that game followed by a game of Nim with a single stone.
A general procedure for converting perfect play at the normal version of an impartial game to perfect play at the misère version would be remarkable, so it’s quite unlikely the generalisation to sequences of impartial games is straightforward.
References and more links
-
[[On Numbers and Games, Conway]]N, specifically:
- Chapter 11: Impartial Games and the Game of Nim
- Chapter 12: How to Lose when you Must
-
[[The Book of Numbers, Conway]]N
- Chapter 10: Infinite and Infinitesimal Numbers, “Nimbers and the Game of Nim”
- “HACKENBUSH: a window to a new world of math” is a playful introduction to some of the esoteric ideas developed in combinatorial game theory.
- “Sprague-Grundy theory” by Gabriel Nivasch for more details on Sprague-Grundy theory.
