Doomscrolling mathematics
TLDR: I forked an open-source project to make MathScroll, which shows you an never-ending list of interesting mathematics content.
Sometime last year I stumbled on a small project called WikiScroll on Hacker News which is a small website that lets you infinitely scroll through Wikipedia articles and their featured images.

While a lot less engaging than Instagram or TikTok, there’s something about the infinite-scroll feature which still makes it fun to use. While a lot of the articles are interesting, the only problem I found is that most of the Wikipedia articles are quite obscure and might not be the most entertain read (unless you’re a big fan of lists of historical batting champions and milk).
Since WikiScroll is open-source, last year I decided to fork it and create MathScroll, which is almost exactly the same except that it only shows Wikipedia pages related to mathematics and science.

I also set up a shortcut on my phone that would hopefully replace the habitual opening of Instagram or Reddit, and this worked great! Even though I was still spending on my phone, I felt marginally better about it since I was still learning something new.
But there’s only so many Wikipedia articles you can skim-read about things you don’t understand before you get bored enough that you might switch back to endlessly scrolling through Instagram or TikTok. To try and combat this, I also added the top 2,500 questions from Math StackExchange and MathOverflow which ended up being a lot more addictive then reading any of the Wikipedia articles.

For good measure, I also added the lecture notes for all of the mathematics courses I’m able to take at university so that I can take a peek at any of them if they look interesting.

Some highlights
These are some of the most interesting questions I’ve come across while scrolling through:
- “What is the smallest set of real continuous functions generating all rational numbers by iteration?”: Imagine a calculator whose display just shows $0$ when you turn it on and has a very limited number of buttons (no numbers!). What’s the fewest amount of buttons you need that apply “nice” functions so that you can eventually get every rational number by pressing some sequence of those buttons?
- “Can one ‘hear’ the shape of a polygon via external reflections?”: Imagine you have a reflective polygon that you cover up with a disc. If the only way you’re allowed to observe the polygon is to shine a laser pointer at it and observe where the ray comes out, can you recover the full shape of the polygon?
- “Fractal behaviour along the boundary of convergence”: This is something I’ve wondered since learning about power series in [[Notes - Analysis I MT22, Power series]]U and [[Notes - Complex Analysis MT23, Power series]]U. Every power series has a so-called “radius of convergence” $R$ where if $ \vert x \vert < R$, $f(x)$ exists, and otherwise $f(x)$ does not exist. But what does $f$ look like when $x$ is very close to $R$? This question is an example of a function where the behaviour around the boundary is fractal-like.
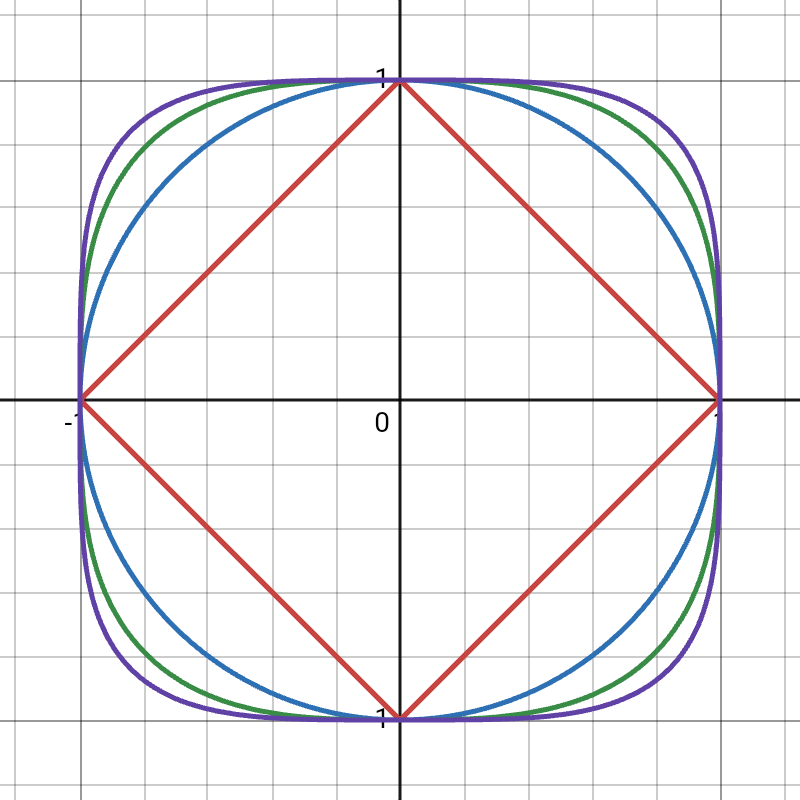
- Squigonometry: The “normal” unit circle is only the unit circle in the 2-norm. If you change your definition of distance between two points, you get different unit circles – for example, if you define the distance as $d((x _ 1, y _ 1), (x _ 2), (y _ 2)) = \vert x _ 2 - x _ 1 \vert + \vert y _ 2 - y _ 1 \vert $, the unit circle looks more like a square, and for other distance functions it can be a squircle, sort of half way between a square and a circle. Interestingly, it turns out you can develop something analogous to trigonometry on these shapes.
- “What are some mathematical topics that involve adding and multiplying pictures?”: Can you solve difficult math problems by formally adding pictures together?
- “Good ‘casual’ advanced math books”
- “Faro shuffle”: There’s a surprising amount of mathematics behind making a perfect shuffle of a deck of cards. This article inspired the blog post [[Number theory at the card table]]B.
- “A transfinite epistemic logic puzzle: what numbers did Cheryl give to Albert and Bernard?”: You might’ve heard of Cheryl’s birthday problem, a logic puzzle where it seems like Albert, Bernard and Cheryl keep on seeming to exchange no information but miraculously determine Cheryl’s birthday. This question presents a majorly juiced-up version whose solution relies on transfinite numbers.

But beware; there is also a lot of the standard Wikipedia/StackExchange fluff of people arguing in the comments about closing questions for being too open or a duplicate of a obscure question asked 12 years ago with a different title and in a different language, and this is especially true of the high-scoring open questions.
Have fun scrolling!