How many ways can you run up the stairs? A puzzle

A short puzzle

You’re a 12th century Italian mathematician who has just moved into their new office. Unfortunately, it is right at the top of several flights of stairs.

There are 7 flights of stairs in total, each of which having 7 steps (starting from the first step raised from the ground, and counting the landing as a final step).

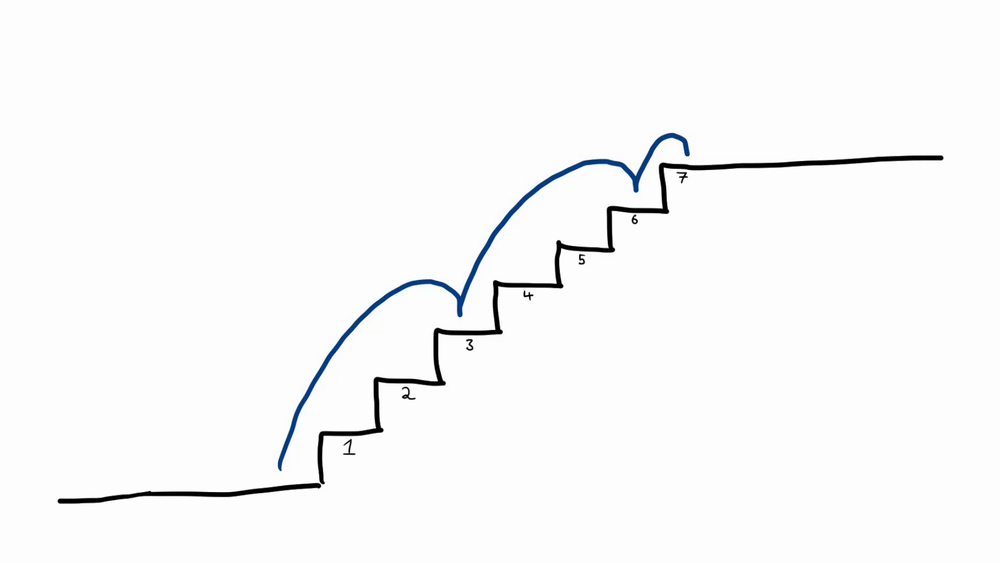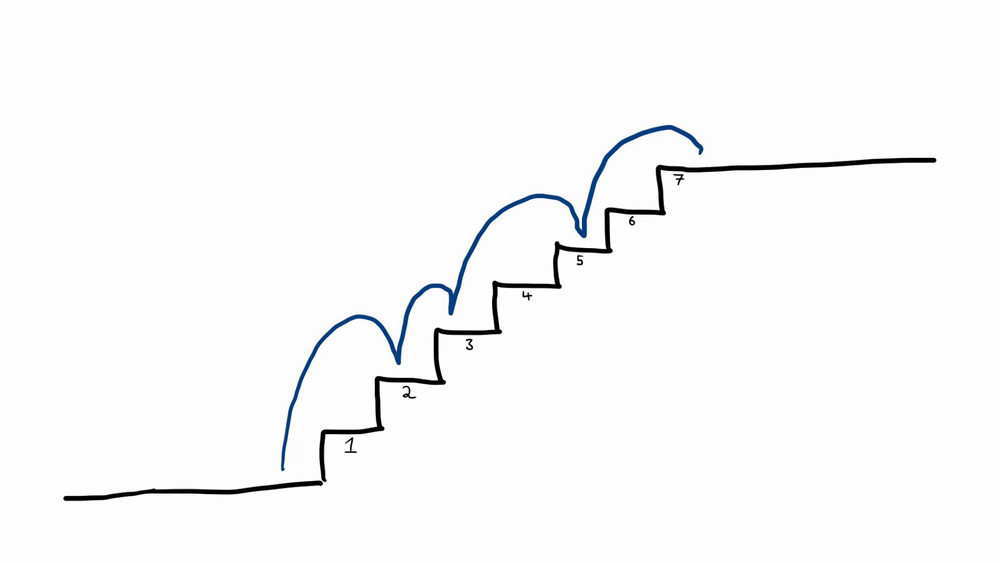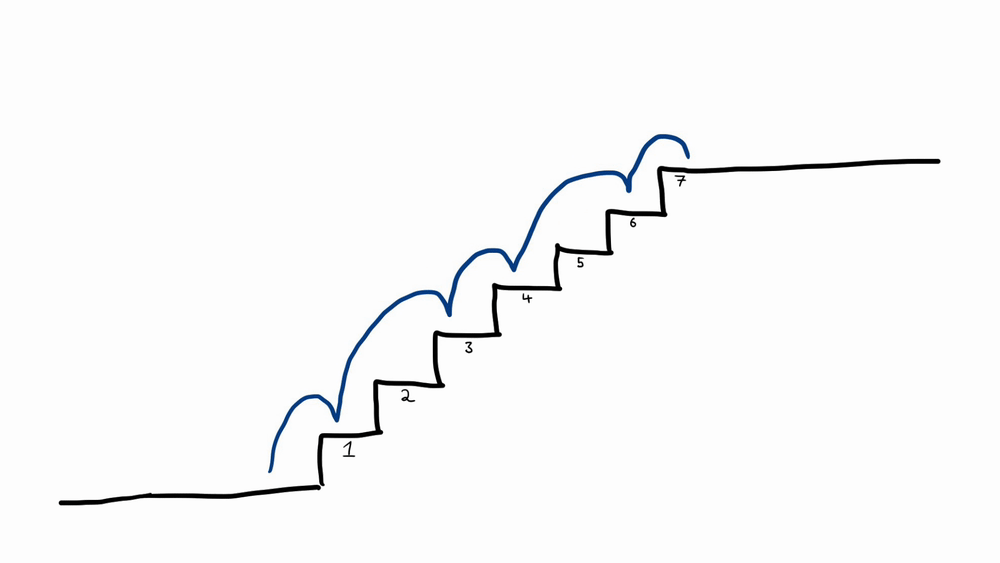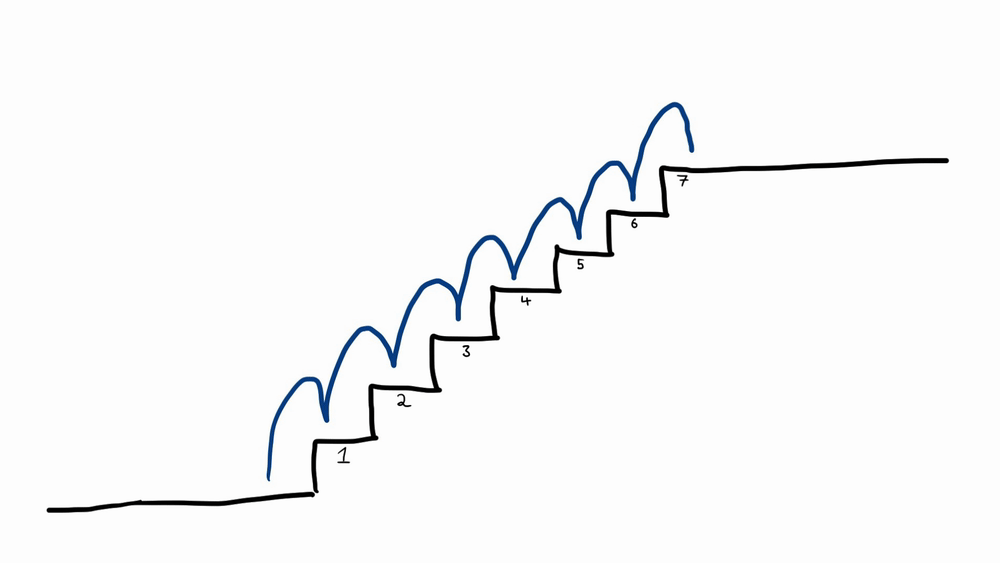
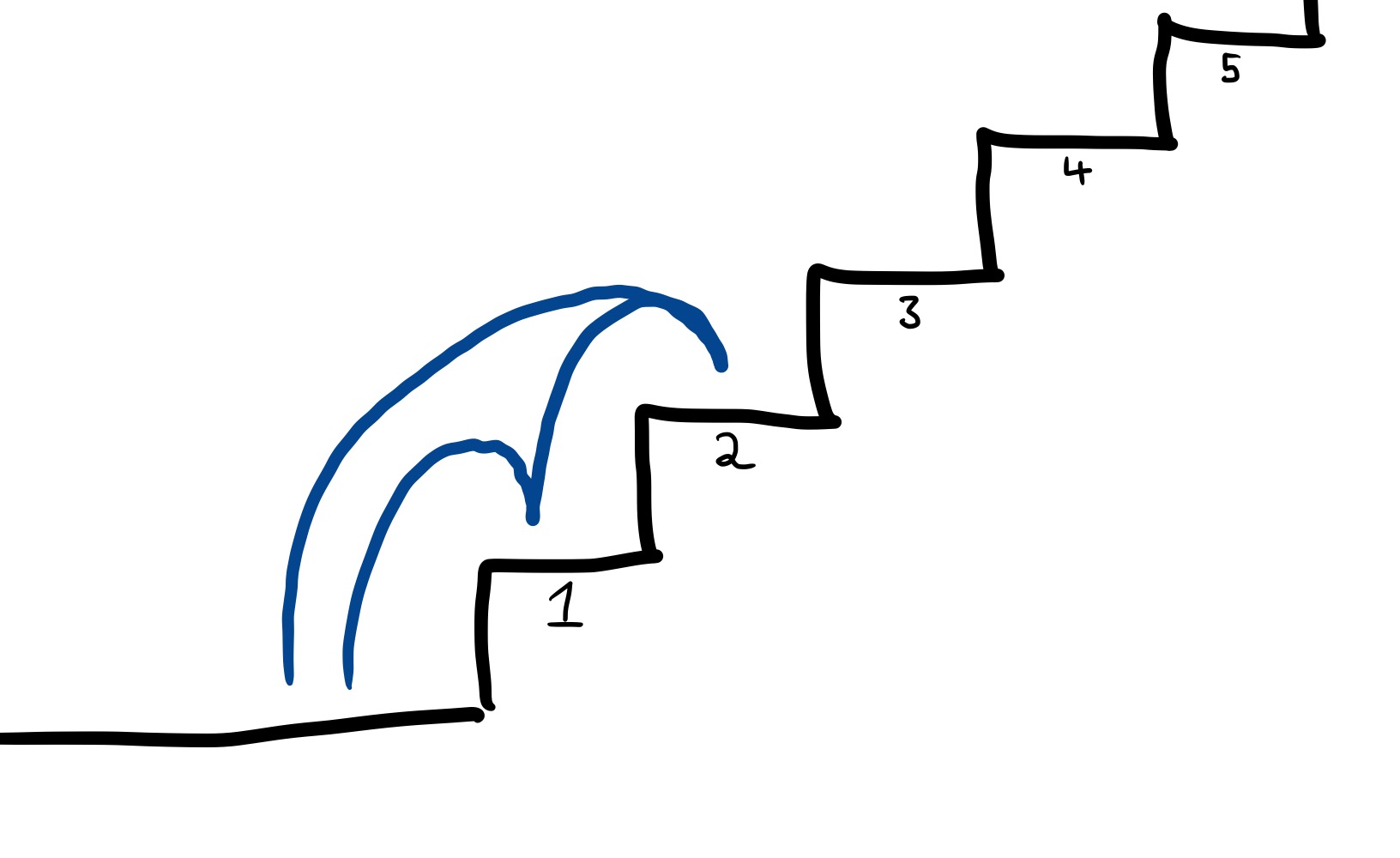
Assuming that you can’t jump over more than 2 steps at a time, how many different ways are there of running up the stairs to get to your office? For example, you could carefully tread on each step one-by-one:

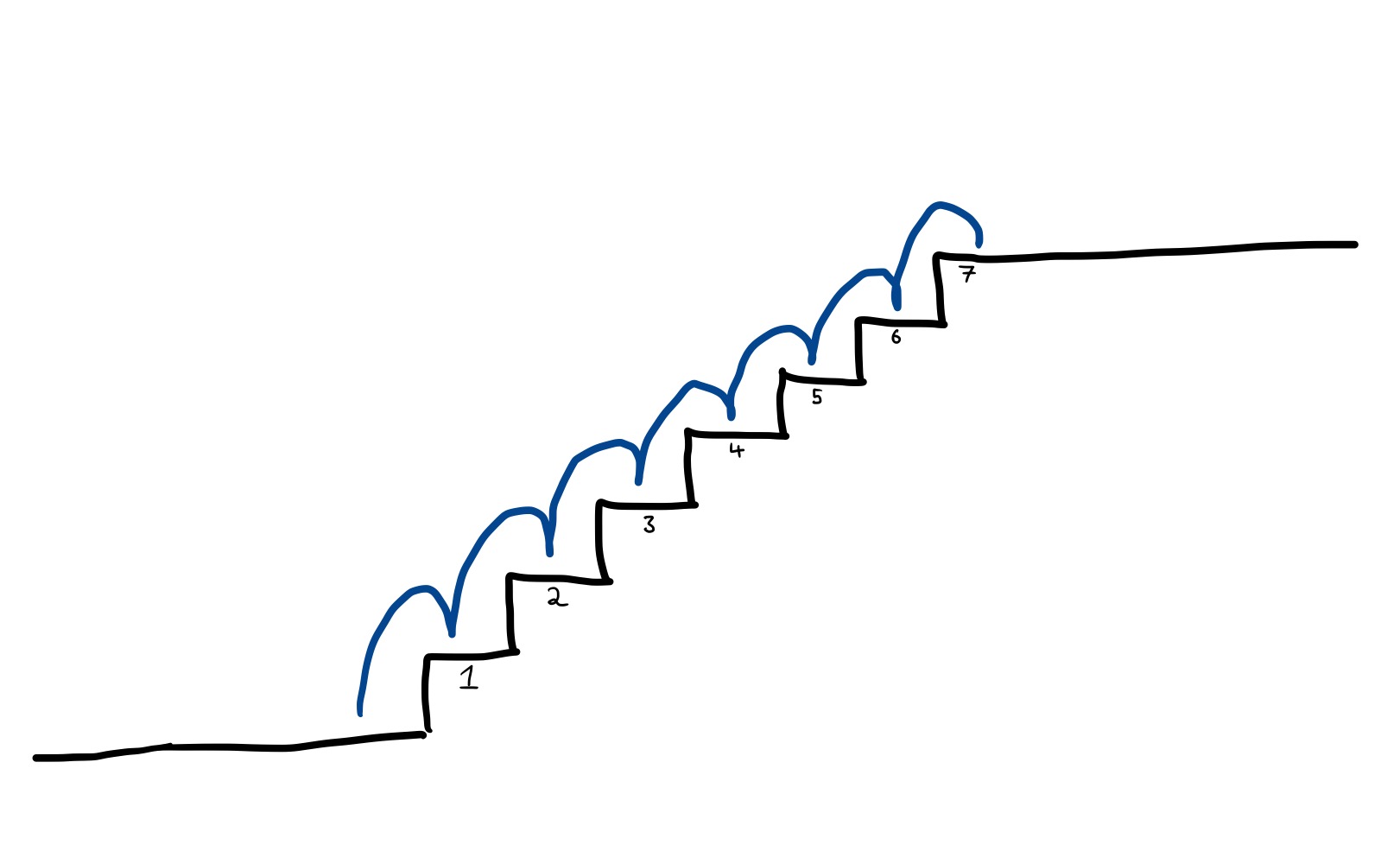
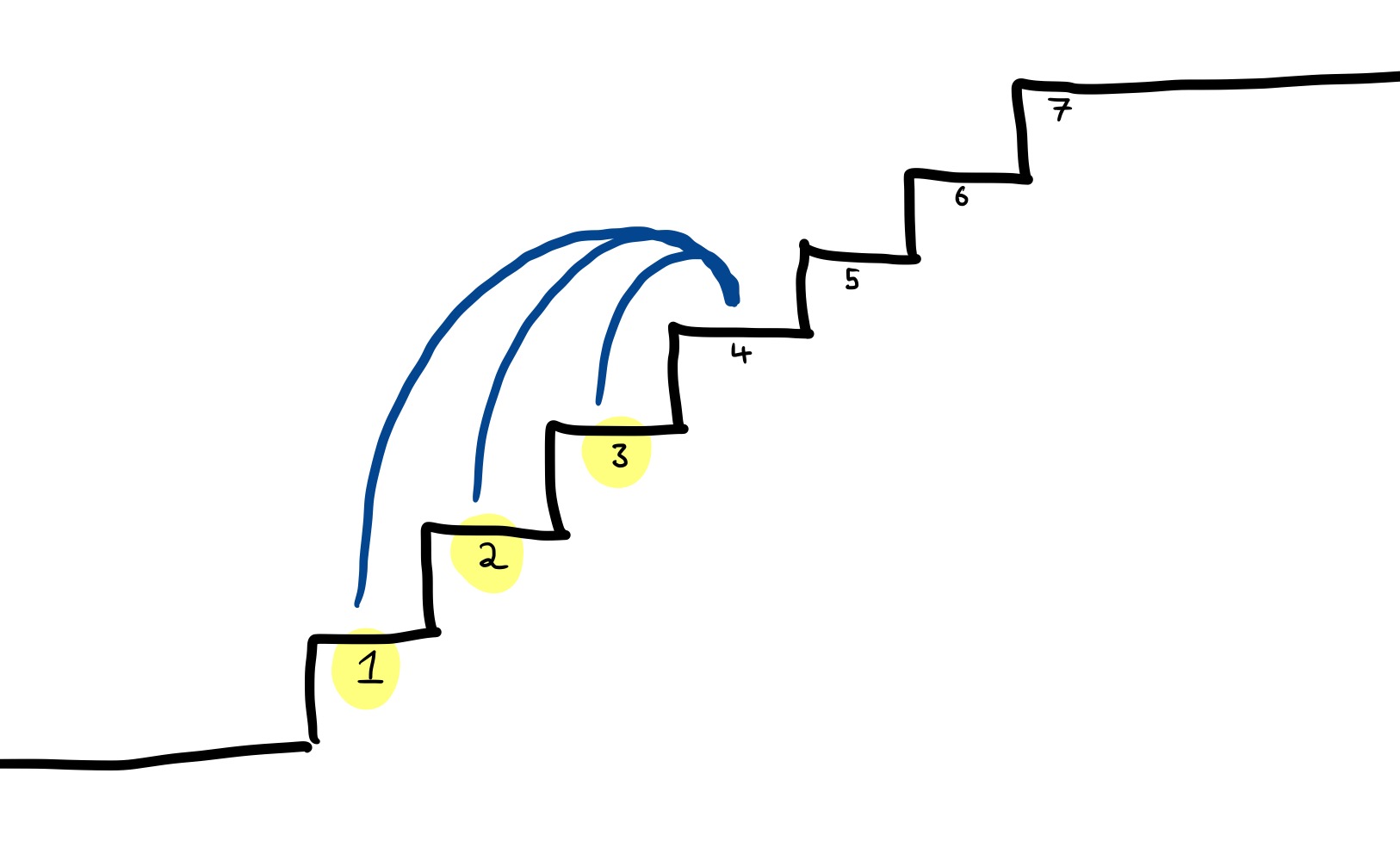
Or clear each flight in three hops:

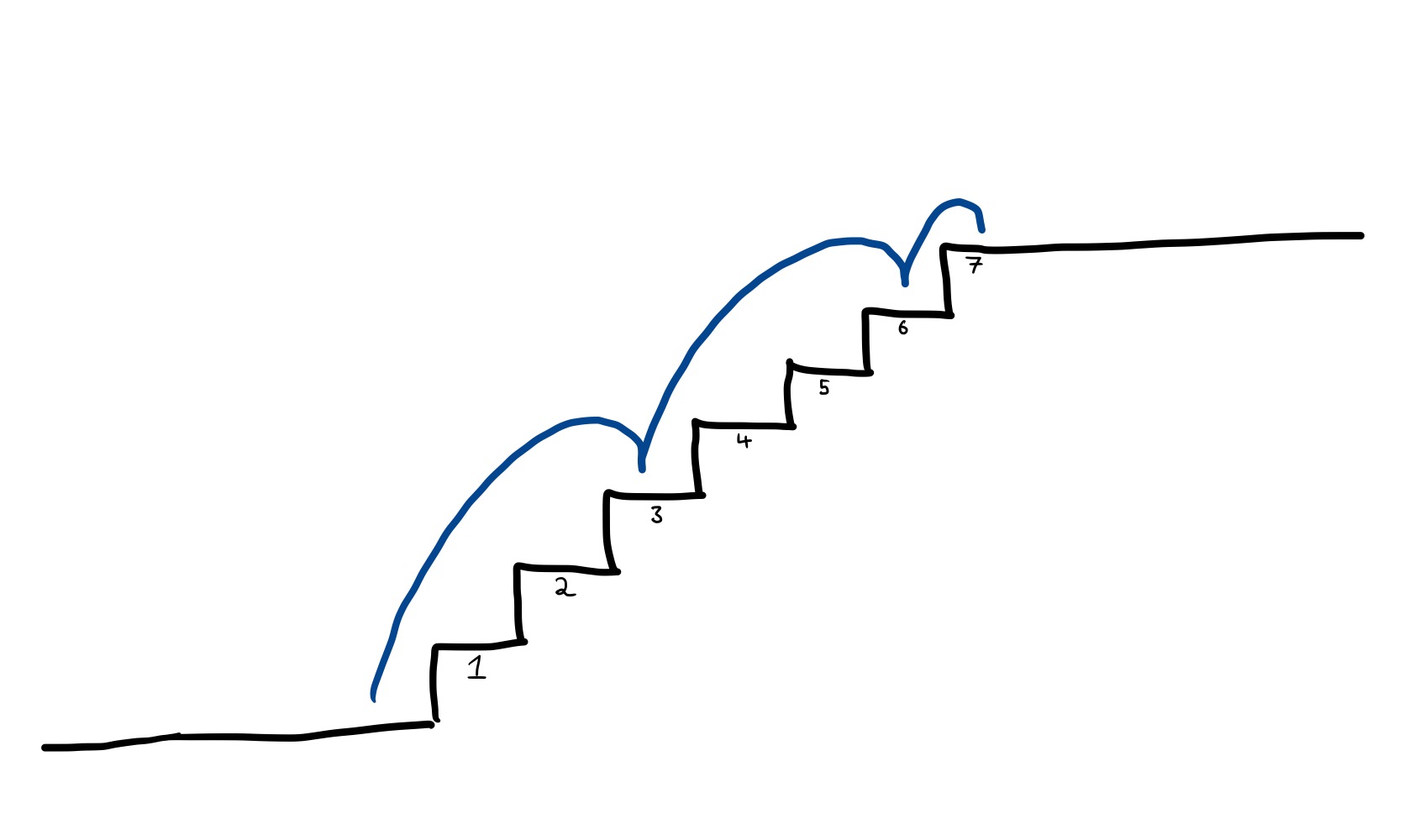
How many ways are there in total? Scroll down to see the solution.

The solution

There are 319,277,809,664 ways. Given how big this number is, it’s not possible to enumerate all of them and so some careful analysis is required!

Running up one flight

There are 44 ways of running up one of the flights.

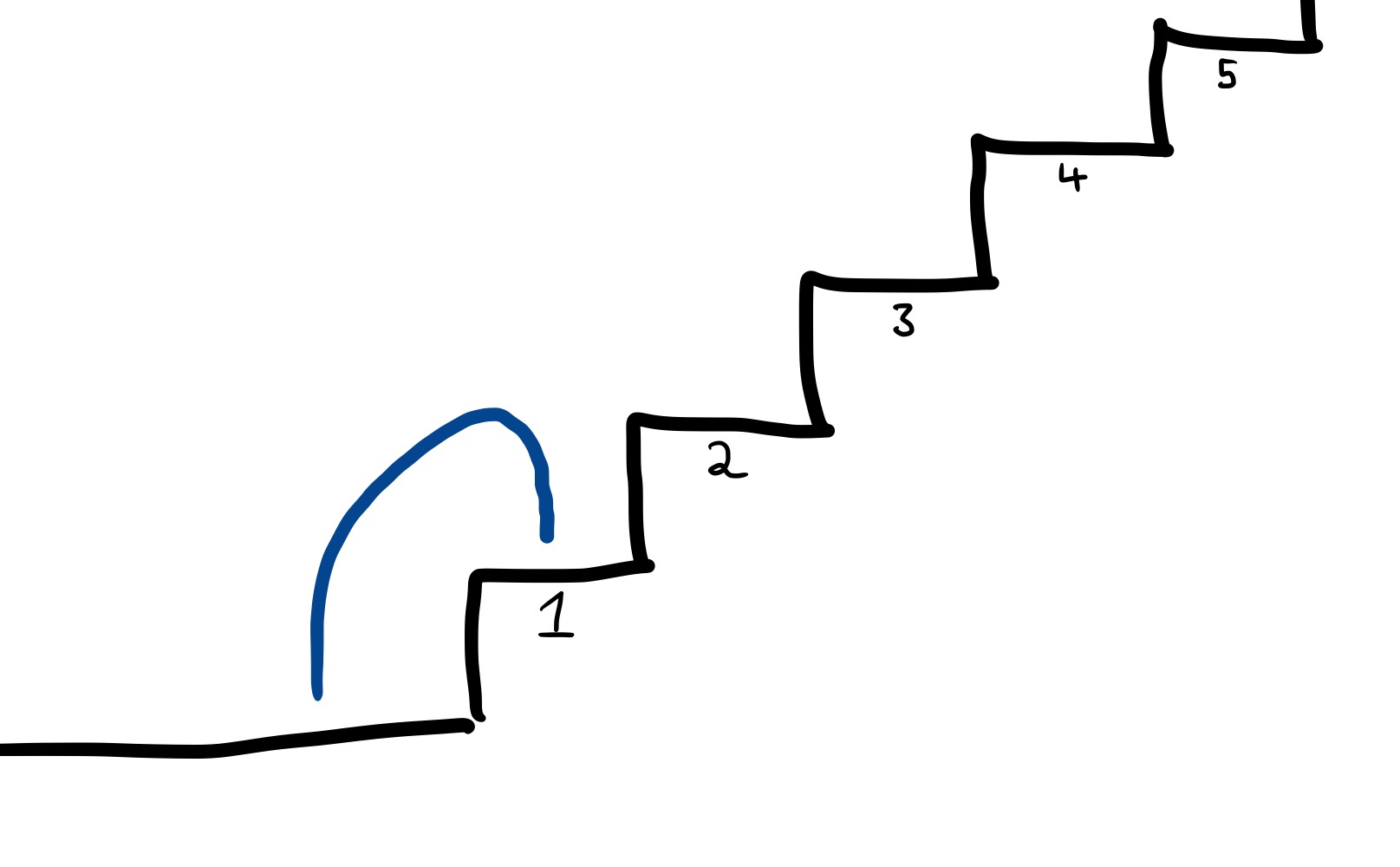
How many ways are there of getting to the first step? There is one way: just stepping onto it ($\bot \to 1$).

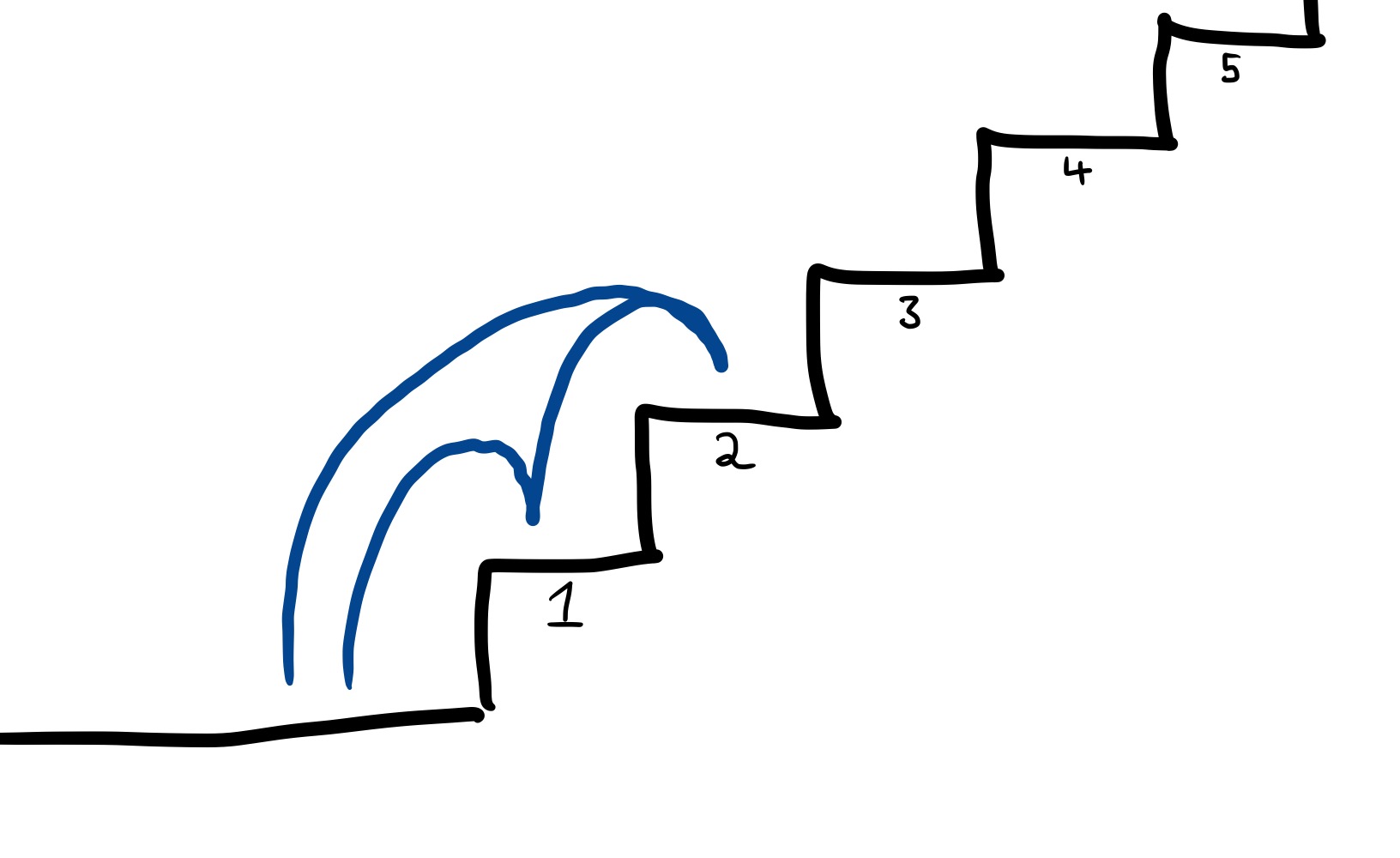
How many ways are there of getting to the second step? There are 2 ways: either go onto the first step and then to the second ($\bot \to 1 \to 2$), or go straight to the second ($\bot \to 2$).

How many ways are there of getting to the fourth step? There are 4 ways: either go one step at a time ($\bot \to 1 \to 2 \to 3$), go first to step one and then to step three ($\bot \to 1 \to 3$), go first to step two and then to step four ($\bot \to 2 \to 3$), or go straight to step three ($\bot \to 3$).

Now things get more complicated, since it’s not possible to go directly to the fourth step from the ground: this would involve skipping over three steps, which is not allowed. But now things are actually easier! Which steps are one leap away from the fourth? Steps one, two and three.

We already know how many ways there are of getting to steps one, two and three: 1, 2 and 4 ways respectively. Therefore we can just add up these three numbers, and this will be the number of ways of reaching the fourth step. Doesn’t this miss situations like going to step one, then to step two and then to step four ($\bot \to 1 \to 2 \to 4$)? No, it doesn’t, since this situation is already accounted for in the number of ways we could reach the second step.

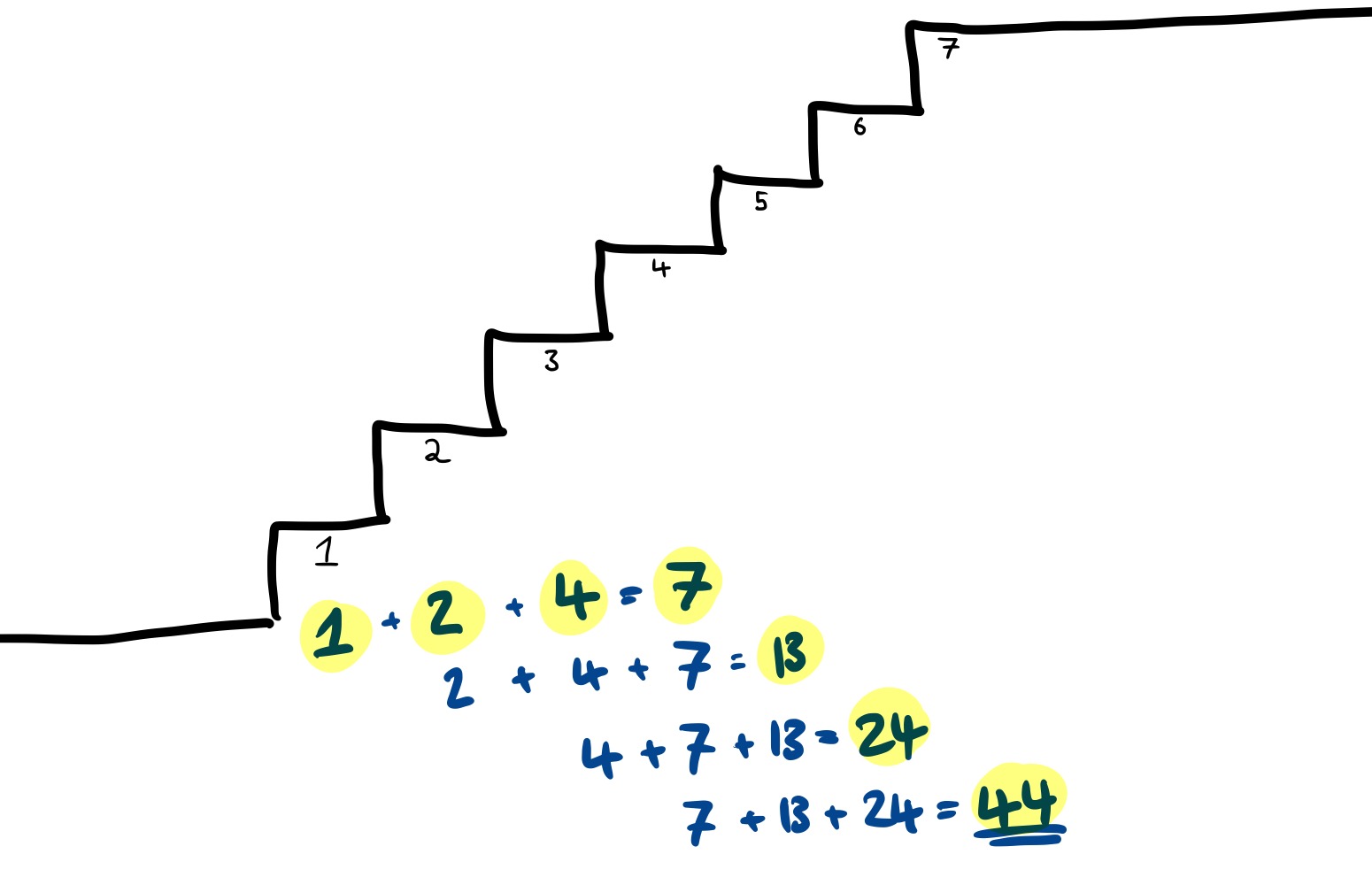
Since $1 + 2 + 4 = 7$, there are 7 ways.

What about the fifth step? Now we add up the number of ways of reaching the steps that could lead to it, which is step two, step three and step four, which can be reached in 2, 4 and 7 ways respectively. Since $2 + 4 + 7 = 13$, there are 13 ways.

For the sixth step, the situation is the same: it can be reached from steps three, four and five, which themselves can be reached in 4, 7 or 13 ways respectively. Since $4 + 7 + 13 = 24$, there are 24 ways.

And finally, how many ways are there of reaching the seventh step, which is also the landing? It can be reached from steps four, five and six, which themselves can be reached in 7, 13 or 24 ways. Since $7 + 13 + 24 = 44$, there are 44 ways of reaching the seventh step, and therefore 44 ways of running up one flight.

Hopefully the pattern should be clear: you just add up the number of ways of reaching the previous three steps. If you could only skip over one step at a time, you would add up the number of ways of reaching the previous two steps.

This should be reminiscent of the Fibonacci sequence. That’s produced exactly the same way, except you start with the two ones and then add up the previous pair to produce the sequence:

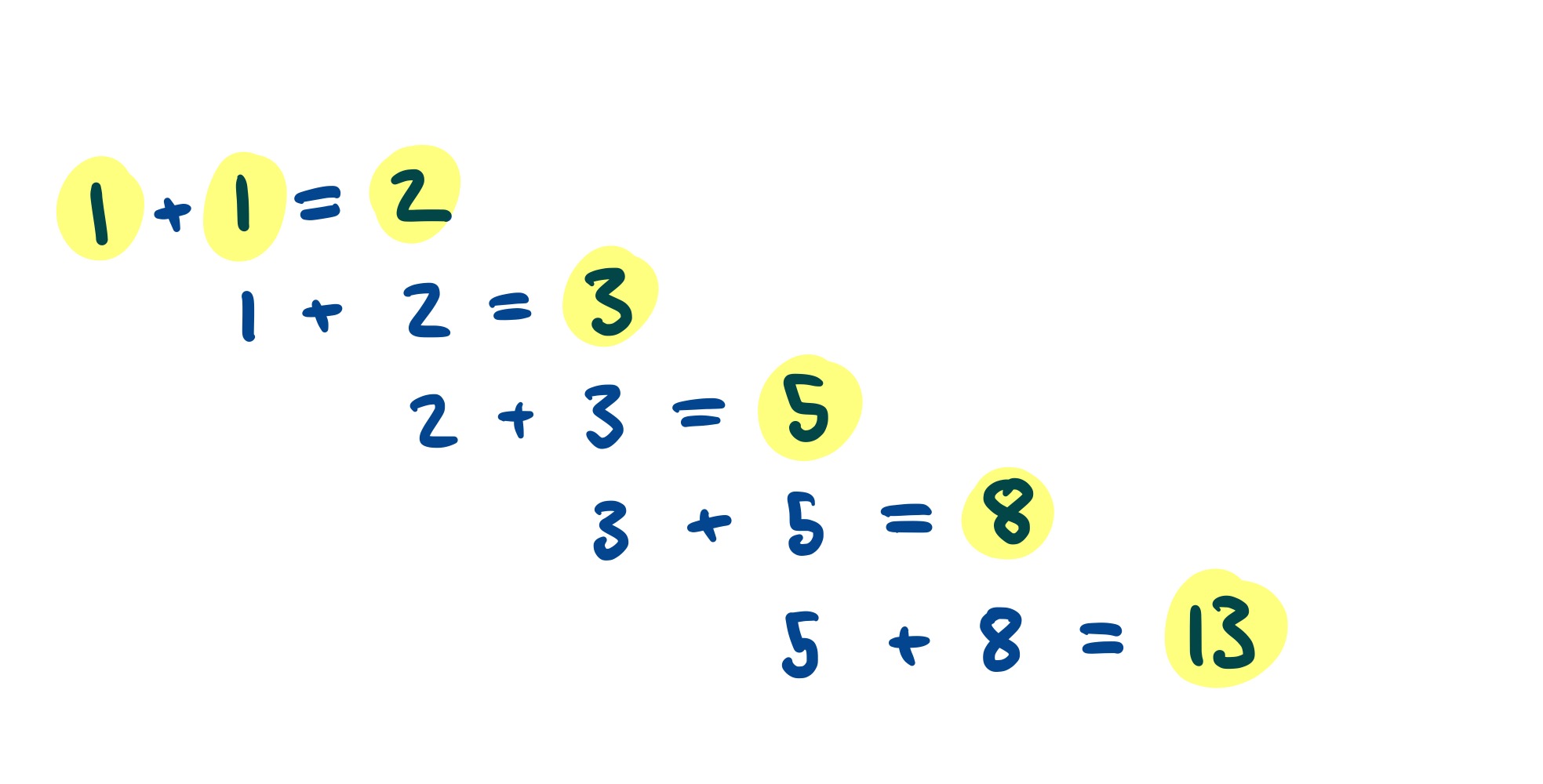
Running up 7 flights

Calculating the number of ways of running up 7 flights is easy now that we know the number of ways of running up one flight. Since we can choose the way we run up each flight independently, there are $44^7 = 319,277,809,664$ ways.

Appendix: code to generate all the ways

Here’s the very slow code I used to generate the list of all 44 ways in lexicographic order. This code will be outrageously slow for bigger sets of stairs, since it checks all possible $2^{\text{steps} - 1}$ ways and then removes those that contains gaps which are too big.

def all_binary_strings(size):
    strings = []
    for i in range(0, 2**size):  # <-- very slow
        strings.append("{0:b}".format(i).zfill(size))
        
    return strings

def all_allowed_strings(size, gap_size):
    return [s for s in all_binary_strings(size) if '0'*(gap_size+1) not in s]

def num_ways(size, gap_size):
    return len(all_allowed_strings(size, gape_size+1))

print("\n".join(all_allowed_strings(6, 3)))

This outputs the following list. The number in the first position is whether or not to step on the first step, the number in the second position is whether to step on the second, and so on. Each number is only six digits rather than seven since the last step must always be stepped on.

Attributions