Extending multidimensional integration in SciPy

• The problem
• A small example: solving a problem with cubature
• Array API support
• Non-rectangular regions of integration
• How it works: $h$-adaptive cubature
• Conclusion

This is a blog post I wrote as part of my three-month internship with Quansight Labs in 2024. It’s also available on the Quansight website, although this page is more up-to-date than that one.

Hi! I’m Olly Britton, an undergraduate studying mathematics and computer science in the UK. This blog post talks about the work I did extending SciPy’s integration facilities as part of a three-month internship with Quansight Labs.

The problem

In one sentence, my work consisted of adding support for multidimensional numerical integration of array-valued functions into SciPy.

Numerical integration, or “quadrature”, is about approximating the value of a definite integral of a function over some region – in other words, estimating the area or volume under a curve. This is in contrast to symbolic integration, which is interested in finding a closed-form for the exact value.

Before this internship, I wondered why you might ever want just an approximation rather than the exact value. But there are many good reasons to prefer numerical integration over symbolic integration: for one, the problem of finding out whether the integral of an arbitrary function has a “closed-form” is actually impossible in general! And even when it is, the results can be hopelessly complicated even for simple functions.

Numerical integration is necessary across many different domains of mathematics and science, especially when faced with real-world problems that are difficult to solve analytically. It’s also one of the oldest mathematical problems that humans have been tackling, with a long history stretching all the way back to Archimedes estimating $\pi$ by approximating the area of a circle.

Before modern computational tools like SciPy existed, people used all sorts of tricks to answer these problems accurately – Archimedes painstakingly approximated the circle as a 96-sided polygon so that he could estimate its area, and there’s a story of Galileo, frustrated with trying to estimate the area under a particular curve mathematically, physically cutting the graph of a function out of metal and weighing the pieces.

Had Galileo or Archimedes been transported to the modern age and given access to SciPy and a computer, they might, after familiarizing themselves with the flourishing PyData ecosystem, check what facilities are now available for integration:

>>> import scipy
>>> help(scipy.integrate)
Integrating functions, given function object
============================================

    quad          -- General purpose integration
    quad_vec      -- General purpose integration of vector-valued functions
    dblquad       -- General purpose double integration
    tplquad       -- General purpose triple integration
    nquad         -- General purpose N-D integration
    ...

After 20 years of maturing as an open source project, SciPy now contains over 15 different functions for numerical integration bundled into the scipy.integrate package, all of which address different but overlapping use-cases and functionality. My task for this internship was to address a small gap in these offerings: improving the support for multidimensional numerical integration (“cubature”), as initially discussed in this SciPy issue in March earlier this year. This culminated in a new function, cubature, which slots into the middle of the “array-valued” and “multidimensional” Venn diagram.

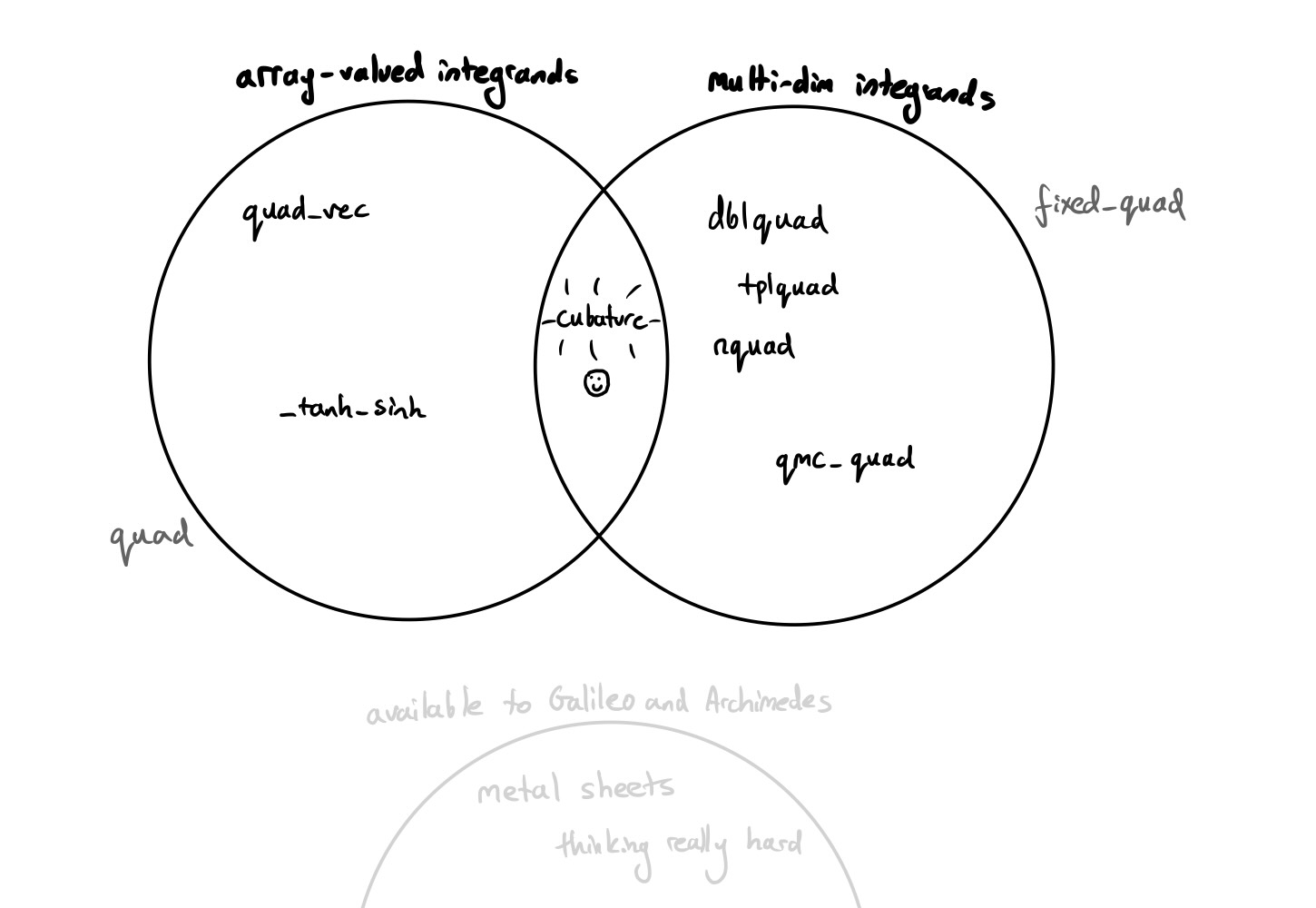
By “multidimensional”, I mean that the routine supports calculating integrals of more than one variable (so volumes and not just areas under a curve), and by “array-valued”, I mean that the routine supports integrands that can return arbitrarily-shaped arrays rather than a single number.

What does it mean to integrate a function that returns an array? It’s the same as if you were to differentiate a function that returns an array: you integrate separately each element of the output. If the function returns a vector (the special case of a 1D array), then this is identical to integrating each component separately:

Previously, there was no function in SciPy that let you efficiently integrate functions that were both multidimensional and array-valued at the same time. For example, quad_vec integrates array-valued univariate functions, while nquad handles scalar-valued multivariate functions. But there was nothing that let you handle integrands that were both.

A small example: solving a problem with cubature

In Pythonville, a small village located in the unit square $[0, 1]^2$, some scientists have come up with a model of rainfall per $\text{cm}^2$ at every $(x, y)$ coordinate, for the next 30 days. They’ve implemented this as a function which looks something like this:

def f(x_arr):
    """
    Given an array of (x, y) coordinates, return an array of predicted 
    rainfall per cm^2 at those coordinates for the next 30 days.
    """
    x, y = x_arr[:, 0], x_arr[:, 1]
    
    # ...magic weather prediction code...
    
    return rainfall_per_cm2

f(np.array([[0.1, 0.2], [0.1, 0.4]]))
# Output:
# array([[0.3524, ..., 0.2235],
#        [0.7881, ..., 0.7873]])

Their implementation of $f$ is vectorized – although $f$ is actually a function of two variables ($x$ and $y$), calculations can be done faster if you can pass it an array of points $f([[x _ 1, y _ 1], [x _ 2, y _ 2], \ldots])$ and the results can all be computed in one call, rather than evaluating one point at a time. In other words, $f$ operates on whole arrays at a time rather than individual elements.

Given this function, the scientists now wish to calculate the total daily rainfall $\mathbf r$ that’s going to fall on the patch around where they live. This is equivalent to the following double integral:

This can be done with the new scipy.integrate.cubature function like so:

from scipy.integrate import cubature

cubature(
    f,      # Function to integrate
    [0, 0], # Lower limits of integration
    [1, 1], # Upper limits of integration
)
# Output: total rainfall on each day
# array([0.5123, 0.4993, ...])

Before the introduction of cubature, this was possible in SciPy but was messier. Here’s how they could have done it with dblquad, which is one of the existing integration functions for multidimensional integrands:

from scipy.integrate import dblquad

# Now assuming f has been implemented as f(x, y, n) rather
# than being vectorized:

results = []

# Rainfall for days 1 to 30
for n in range(30):
    res, err = dblquad(f, 0, 1, 0, 1, args=(n,))
    results.append(res)

Here, the usefulness of supporting array-valued integrands should be clear: it lets you avoid for-loops like this one, and this means that the code can more effectively utilize the underlying array library (in this case, NumPy). This allows the 30 integrals required for each day to be computed simultaneously, rather than one at a time.

dblquad’s implementation uses a wrapper around a FORTRAN 77 package called QUADPACK. The version in SciPy was written in 1984! (Although, while I completed the internship, the version of QUADPACK in SciPy was actually translated to C). The fact the package being used is from 40 years ago is not a bad thing – if anything, it shows that it is a robust piece of software. But ignoring 40 years of growth in scientific computing it is not without its drawbacks.

Array API support

One feature of the new cubature function that would be hard to support with dblquad is that it also supports the array API standard. For a good primer on what this means, see The Array API Standard in SciPy. In brief, a lot of SciPy’s code relies heavily on NumPy, which provides the array data structure used to efficiently implement most of the algorithms SciPy offers. But a considerable amount of recent effort has meant that lots of SciPy functions are now array-agnostic – you can give these functions arrays from other compatible libraries, like PyTorch or CuPy, and they will also work:

import torch

# Now assuming f is implemented with PyTorch

f(torch.Tensor([[0.1, 0.2], [0.1, 0.4]]))
# Output:
# tensor([[0.3524, ..., 0.2235], [0.7881, ..., 0.7873]])

cubature(f, [0, 0], [1, 1])
# Output:
# tensor([0.5123, 0.4993, ...])

This is good news for lots of reasons. For one, it means you can do array operations on the GPU rather than the CPU. This would’ve been quite difficult to add to dblquad and the rest of the functions from the QUADPACK family, and not just because QUADPACK actually predates the first GPU by many years!

Non-rectangular regions of integration

The implementation of this has yet to be merged into SciPy. It’s currently an open PR here.

Another feature of cubature relates to the kinds of integrals it can calculate. The examples so far have focussed on integrals over rectangular regions, but it’s also common to see integrals over non-rectangular regions. These are problems where the limits are functions rather than just constants.

For example, one way of phrasing Archimedes’ problem of calculating $\pi$ is that he was, without knowing it, approximating the following integral:

cubature also supports these kind of problems, where you have arbitrary functions in the limits:

cubature(
    f=lambda x: np.ones(x.size[0]),   # f is the constant 1 function
    a=[-1],
    b=[1],
    region=[
        lambda x: (
            [-np.sqrt(1-x[:, 0]**2)],
            [ np.sqrt(1-x[:, 0]**2)],
        ),
    ],
)
# Output:
# array([3.14159])

You can even use infinite limits before the functions and it will still work. For example:

cubature(
    f,
    a=[0], b=[np.inf],
    region=[
        lambda x: (
            [0],
            [x[:, 0]],
        ),
    ],
)
# Output:
# array([0.3926...])

Again, this could also have been previously using existing routines like dblquad and nquad, but there was no existing functionality for integrating array-valued integrands over arbitrary regions. Also, the approach that dblquad takes to handling double integrals (namely, treating them as a series of nested 1D integration problems) has some disadvantages compared to the approach that cubature takes.

How it works: $h$-adaptive cubature

cubature isn’t fixed to using one particular mathematical approach to numerical integration, like the trapezoid rule. Instead, it instead accepts a parameter called rule, which is a class with two methods: estimate(f, a, b) and estimate_error(f, a, b) (or a string, which is an alias for a particular class).

There might be rule classes which implement the trapezoid rule or Gauss-Legendre quadrature, both of which sample the function $f$ being integrated at a fixed number of points and do some calculations to turn these evaluations into an estimate for the integral over that region. These rules by themselves aren’t very flexible and so might not give very good approximations – the job of cubature is then to work out how to repeatedly apply each rule over different subregions in order to get an accurate estimate of the integral.

For example, the simplest version of trapezium rule evaluates the function at the start and end of an interval, and estimates that the area of the function is roughly the same as the area of the trapezium formed by connecting up these two points.

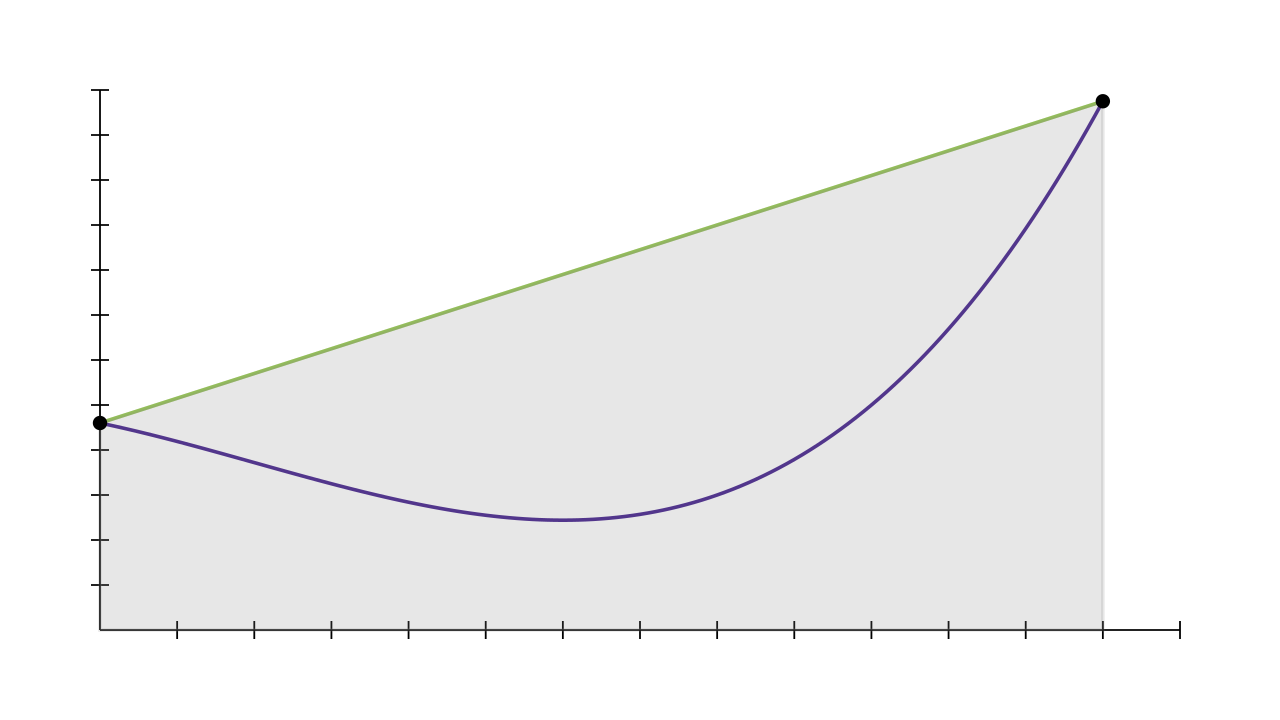
If the number of points that $f$ is evaluated at remains constant for each call to rule, then you’d expect that applying the rule over a smaller region would give more accurate estimates. This forms the basis of “$h$-adaptive” algorithms: estimate the integral over the big region requested by the user, and if the error is too high, split the interval in half and apply the rule to each of the subregions separately. Then you continue dividing the region with the highest error until the tolerance is reached.

If instead you increase the number of points that $f$ is evaluated at for each call to rule while keeping the size of the region fixed, this forms the basis of a “$p$-adaptive” algorithm. $h$-adaptive algorithms and $p$-adaptive algorithms are named for the things they vary: $h$-adaptive algorithms vary the size ($h$) of the region being integrated, and $p$-adaptive algorithms vary the number of points ($p$) being used.

For $h$-adaptive cubature in higher dimensions, the process is almost identical. Rather than splitting an interval in two, you now split a rectangular patch of the function into four. Then you refine the estimate over the subregions which have the highest estimated error.

That’s the premise behind the algorithm. In more than two dimensions, things get harder to visualise, but the idea is the same: compute an estimate of the integral over some region, and if the error is still too high, split that region into many smaller regions and repeatedly apply the rule to the small regions with high error. But the basic idea is still the same: stripped back, the key loop in the actual source of cubature reads something like this:

# Find the estimate of the integral over the big region requested
# by the user
est = rule.estimate(f, a, b)
err = rule.estimate_error(f, a, b)

regions = [Region(a, b, est, err)]

# While the error is still too high...
while np.any(err > atol + rtol * np.abs(est)):
    # Find the region with the largest error
    region = heapq.heappop(regions)

    # Refine this region into several subregions
    for (a_k, b_k) in find_subregions(region):
        # Calculate the estimate over this subregion
        subregion_est = rule.estimate(f, a_k, b_k)
        subregion_err = rule.estimate_error(f, a_k, b_k)

        est += subregion_est
        err += subregion_err

        heapq.heappush(regions, Region(a_k, b_k, subregion_est, subregion_err))

    # Remove old estimate so we don't double count
    est -= region.est
    err -= region.err

Another piece of the puzzle is how arbitrary regions are handled. It’s not immediately obvious how you’d apply this algorithm to integrals like this one from earlier:

The issue here is that the region being integrated over is no longer rectangular – here it’s shaped like an infinitely large pizza slice extending out from the origin. To tackle this, you need some consistent method of subdividing non-rectangular regions.

One way of doing this is quite simple: you apply a coordinate transformation to the integral which turns it into an equivalent integral over a rectangle like $[-1, 1]^n$, and then you can subdivide like before.

Since these integrals are equal, cubature can calculate the rectangular integral using the algorithm above, and subdivisions in these transformed coordinates correspond to useful non-linear subdivisions in the original coordinates.

Conclusion

Prior to this internship, the prospect of contributing to a large open source project as a first-time contributor had felt a little daunting – but I have had an extremely rewarding experience over the last three months. It’s been a unique opportunity to interact with an incredibly positive and flourishing community, learn very practical skills for a future career in software engineering and open source, and simultaneously learn about a very interesting topic.

I’d like to thank my mentors Evgeni Burovski and Irwin Zaid for all of their generous help and support, and Melissa Mendonça for coordinating the internship itself and offering lots of helpful advice. I would also like to thank the many members of the SciPy community who took their time to review my PRs, including Lucas Colley, Jake Bowhay and Ilhan Polat. And finally, many thanks to Quansight Labs for providing such a distinctive and fulfilling opportunity.