Finding the shortest route between every Oxford college
Some runs can be physically hard: the route might be very long, there might be lots of elevation gain, the path might be muddy. But fairly few runs are computationally hard in that you have to solve a difficult optimisation problem in order to run them. The travelling salesman problem (or “TSP”) is a graph-theoretical problem that leads to computationally hard running routes. Formally, it is defined like so:
\[\sum^{k} _ {i = 1} w(v _ {i-1},v _ i)\]TSP (formally): Let $G = (V, E, w)$ be a weighted graph where:
- $V$ is a finite set of vertices
- $E \subseteq V \times V$ is a finite set of edges, a symmetric relation on vertices
- $w : E \to \mathbb R _ {\ge 0}$ is a symmetric function assigning each edge $(u, v) \in E$ a positive weight
A tour in $G$ is a sequence of vertices $(v _ 0, \ldots, v _ k)$ such that $v _ 0 = v _ k$ and each vertex occurs in $V$ exactly once. Define the weight of a tour as
Call a tour optimal if it is the lowest weight among all possible tours. Given such a $G$, can you find an optimal tour?
But informally, it asks the question:
TSP (informally): Given a list of landmarks and distances between them, can you find the shortest-distance route that visits every landmark?
So called the “travelling salesman” problem because it lets you save the most amount of fuel as you drive from city to city selling your product, the TSP is very famous in computer science as a prototypical example of a hard optimisation problem: it’s very likely that it’s impossible to write a computer program that does much better than checking every possible route.
The travelling scholar problem
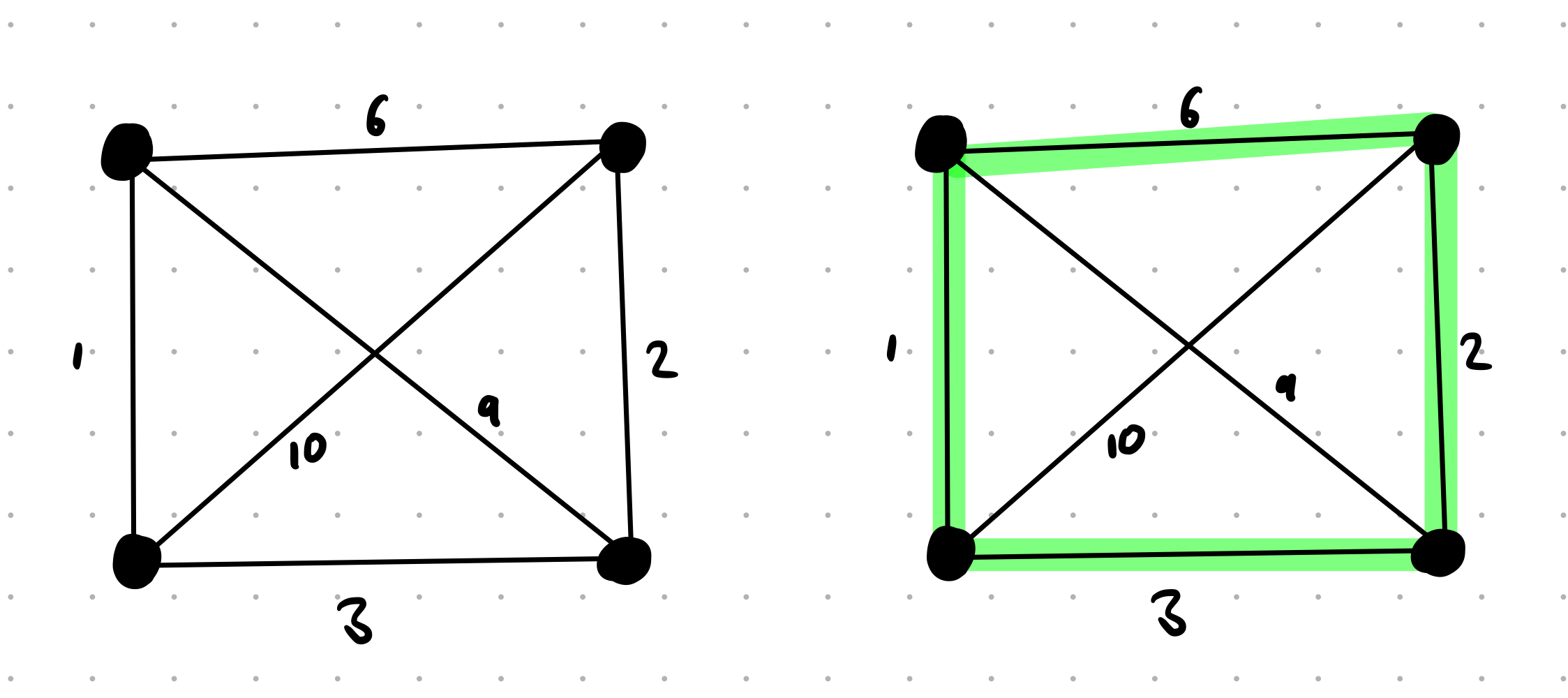
Many online examples for the travelling salesman problem use abstract examples, like finding the shortest TSP tour of a graph like this:
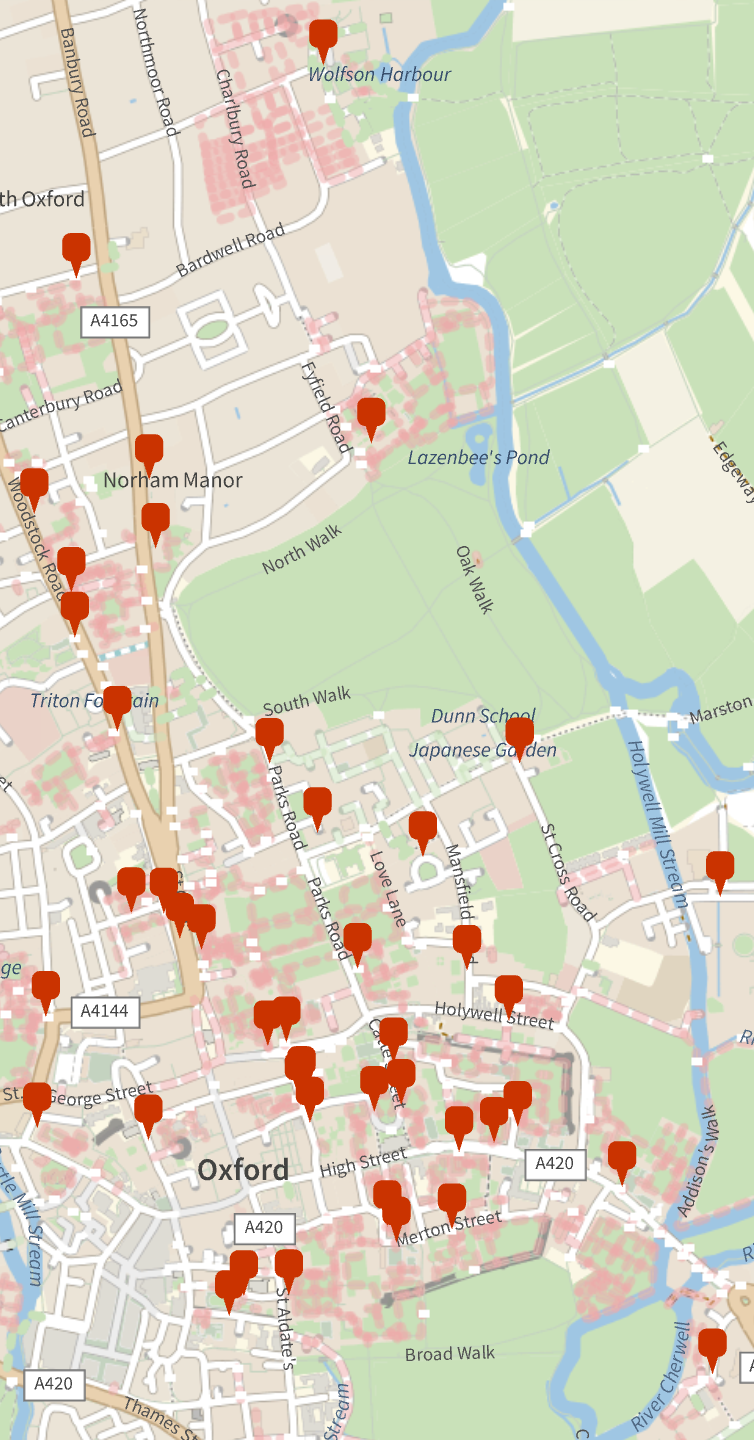
Here’s a more concrete example. This is a plot of every college and permanent private hall in Oxford:
The travelling salesman problem asks: what is the shortest running route that visits every college? Here is one optimal solution:
- Christ Church
- Pembroke College
- Oriel College
- Corpus Christi College
- Merton College
- The Queen’s College
- St Edmund Hall
- University College
- St Hilda’s College
- Magdalen College
- St Catherine’s College
- Linacre College
- Mansfield College
- Harris Manchester College
- New College
- Hertford College
- All Souls College
- Brasenose
- Lincoln College
- Jesus College
- Exeter College
- Balliol College
- Trinity College
- Wadham College
- Reuben College
- Keble College
- Lady Margaret Hall
- Wolfson College
- St Hugh’s College
- Kellogg College
- Wycliffe Hall
- St Antony’s College
- St. Anne’s College
- Green Templeton College
- Somerville College
- Regen’s Park Colelge
- St Cross College
- Blackfriars
- St John’s College
- Worcester College
- Nuffield College
- St. Peter’s College
- Campion Hall
- Christ Church
And here’s what actually running it looks like:
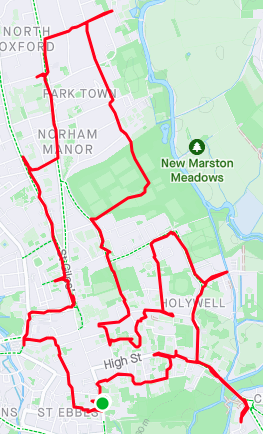
Of course, this is not unique: it doesn’t matter if you start and end at any other college or run around in reverse since it will still be the same distance. This solution is optimal according to the software I used, assuming that it knows the accurate walking distances between each college. It’s possible that there’s shortcuts that it doesn’t know about (e.g. in the above it’s actually possible to go diagonally across the park next to “New Marston Meadows”) and this could change the solution.
Cooking your own optimal tours at home
It would be very easy to come up with a route between every college by hand, but you wouldn’t know that it was optimal. Here’s how you can use a computer to find a guaranteed optimal solution.
- Ingredients: I used Wolfram Language (formely Mathematica), but if you don’t have access to this, it would also be possible to find a tour using free and open source tools like OR-Tools (Python, C# or Java) as well as manually calculating all the $N^2$ pairwise distances for the distance matrix.
- Make a spreadsheet of the coordinates for every landmark you want to visit. I did this using Google Sheets and Google Maps. Google Maps has a very handy feature where if you right click anywhere, you can immediately copy the coordinates of that point to the clipboard.

-
Convert this into a list that can be used in Wolfram Language. I did this by writing an Google Sheets formula which would generate the strings you see on the right in the image above. There’s probably much better ways of doing this but I’m not very familiar with Wolfram. I used the following formula for this:
=CONCATENATE("{", char(34), A1, char(34), ", ", "GeoPosition[{", B1, "}]", "},") -
Use the following Wolfram Language program to actually calculate the optimal tour:
namedCoords = {...the list from above...};
distanceFunc[i_, j_] := TravelDistance[{namedCoords<a class="wikilink wikilink-unknown unknown-text" href="/404">[[<span class="unknown-text">i, 2</span>]]<sup><strong>?</strong></sup></a>, namedCoords<a class="wikilink wikilink-unknown unknown-text" href="/404">[[<span class="unknown-text">j, 2</span>]]<sup><strong>?</strong></sup></a>}, TravelMethod -> "Walking"];
tour = FindShortestTour[Range[Length[namedCoords]], DistanceFunction -> distanceFunc, PerformanceGoal -> "Quality"];
namedTour = namedCoords[[#]] & /@ tour<a class="wikilink wikilink-unknown unknown-text" href="/404">[[<span class="unknown-text">2</span>]]<sup><strong>?</strong></sup></a>; namedTour
-
There are two important things in the above code:
- Firstly, the
TravelMethodneeds to be set to"Walking"so that it will use walking distances rather than driving distances. - Secondly, setting
PerformanceGoalto"Quality"ensures that the solution is optimal rather than an approximation. If you have a lot landmarks, you might need to set the goal to"Speed"instead for it to find a route in any reasonable amount of time. After all, it is a hard problem!
- Firstly, the
- Look at the list and then plot the route. The above program prints out a list of landmark names. I then used plotaroute.com to create a GPX file which routed between each of the colleges in order.
- Go and run/walk/drive it! If you’re lacking motivation while you’re out actually completing it, remember out of all possible running routes you could’ve made, this one will be the shortest.
Why is the TSP difficult?
One way of measuring the difficulty of problems is the idea of a complexity class. These are ways of categorising problems by measuring the amount of time or space that’s needed to solve them according to how complicated their input is.
Two very important classes are $\mathbf P$, the set of all problems solvable in “polynomial time”, and $\mathbf{NP}$, the set of all problems solvable in “nondeterministic polynomial time”. Skimming over a lot of detail, if a problem is in $\mathbf P$ it means that there’s a computer program that solves it in an amount of time that scales polynomially with the size of the input. Polynomial growth roughly means that the time it takes is given by a formula like $\text{time taken} = \text{size of input}^n$ for some $n$ that doesn’t depend on the input.
If a problem is in $\mathbf{NP}$, it means that it has an algorithm where the amount of time it takes scales exponentially with the size of the input (sort of). For example, the time taken might be given by a formula like $\text{time taken} = n^{\text{size of input}}$ where $n$ is once again a number that stays the same (and is greater than $1$). This is much faster than polynomial!
To be slightly more specific, $\mathbf P$ and $\mathbf{NP}$ also contain all problems where the time it takes to solve them grows slower than polynomially or exponentially. As a consequence of this definition, every problem that is in $\mathbf P$ is also in $\mathbf{NP}$ since exponential growth always beats polynomial growth in the long run. Written mathematically, this says $\mathbf P \subseteq \mathbf{NP}$.
These classes are concerned with “decision problems”: given some input, an algorithm should output true or false depending on whether some condition is met. This includes problems like determining whether a number is prime, checking whether a list is sorted, or seeing if graph admits a Hamiltonian cycle.
The TSP isn’t strictly a decision problem, since a solution to the TSP is instead a path instead of a simple yes or no answer. But it’s possible to convert the TSP into a decision problem by constructing a related question: “given this weighted graph $G = (V, E, w)$ and a positive number $k$, is there a travelling salesman tour with weight less than $k$?”. This question has a yes or no answer and so is a decision problem.
It turns out that you can give an exponential time algorithm for this problem and so it belongs in $\mathbf{NP}$. But this isn’t quite enough to say that the TSP has no algorithm that is quicker than exponential, since to do this, you need to be able to say that the TSP is also not in $\mathbf{P}$.
If the TSP were not in $\mathbf P$, it would imply that $\mathbf P \ne \mathbf{NP}$, which is perhaps the biggest and most famous unsolved problem in computer science. As far as we know, it could be that $\mathbf P = \mathbf{NP}$, and that there is some polynomial time algorithm for TSP, but we just don’t know what that algorithm is. But all evidence so far points towards this not being the case.
Appendix: Some specifics
The tour above uses the walking distance calculated by the TravelDistance function between each college, rather than the straight-line distance. This is to avoid routes that superficially seem to minimise the distance, but actually involve impossible cuts through buildings and grass you’re not supposed to walk on. Interestingly, this actually makes the problem harder – if you’re using straight line distance, then it’s actually an instance of the “metric travelling salesman problem” which is a little easier to solve. For example, the metric travelling salesman problem admits quick approximation algorithms. These are polynomial time algorithms which give you a solution to the TSP, not necessarily optimal, but guaranteed to be within some factor of the optimal. The Christofides algorithm is an approximation algorithm for the TSP which is guaranteed to be at most $1.5$ times the length of the optimal solution.
I used the following coordinates for the colleges. I tried to pick the front of the colleges since the location you get from just typing the name into Google Maps would sometimes be at a random spot inside the college, which might mess up the walking distance calculation made by Wolfram.
| College | Longitude, Latitude |
|---|---|
| Christ Church | 51.75020082543448, -1.2566674102132913 |
| All Souls College | 51.75343005838777, -1.2535421840374497 |
| Jesus College | 51.75355829550146, -1.2563561206347236 |
| Harris Manchester College | 51.75570974565153, -1.2517368067224688 |
| Hertford College | 51.75413914302557, -1.2537729448834982 |
| Mansfield College | 51.7576346663018, -1.252968999604003 |
| Linacre College | 51.75922245440031, -1.2503182622363669 |
| St Catherine’s College | 51.7569560469285, -1.2448284803107663 |
| St Hilda’s College | 51.74886513448575, -1.2450390380822247 |
| St Edmund Hall | 51.75306261199469, -1.2503734001348958 |
| The Queen’s College | 51.75279045166381, -1.2510212502819025 |
| University College | 51.75263560778315, -1.2519799786046888 |
| New College | 51.754856449240314, -1.2506139859520802 |
| Merton College | 51.75132657767746, -1.2521736550639375 |
| Campion Hall | 51.74985372046716, -1.258275242760393 |
| Exeter College | 51.75365371291273, -1.2562940981724775 |
| Corpus Christi College | 51.75110042582413, -1.2536934627049032 |
| St. Peter’s College | 51.752834313714196, -1.2604859882110688 |
| Nuffield College | 51.753037984505816, -1.26353223356112 |
| Oriel College | 51.75137850581435, -1.2539442321908754 |
| Pembroke College | 51.75019381391679, -1.2578721890536433 |
| Worcester College | 51.75492721828783, -1.2632964159183049 |
| Regen’s Park Colelge | 51.756683990593, -1.2609539167942967 |
| Reuben College | 51.758043352078516, -1.255855936159926 |
| Somerville College | 51.75975987446296, -1.2613391652668022 |
| Green Templeton College | 51.76135742874665, -1.262502359524542 |
| St. Anne’s College | 51.762115950301705, -1.2625991961845513 |
| Wycliffe Hall | 51.76286088344048, -1.2602895767179565 |
| Kellogg College | 51.76402677743072, -1.2604664652219917 |
| St Antony’s College | 51.76345024923746, -1.263612658298954 |
| St Hugh’s College | 51.76743490692448, -1.2624612514859312 |
| Wolfson College | 51.771054769081786, -1.2556974680921367 |
| Lady Margaret Hall | 51.76464338450338, -1.2543814764066628 |
| Blackfriars | 51.756251586014706, -1.2596273012134334 |
| St Cross College | 51.75667802506971, -1.2600647545638362 |
| St John’s College | 51.75605832863825, -1.2590340001478713 |
| Balliol College | 51.75442804120147, -1.2572171251803663 |
| Wadham College | 51.75574172460674, -1.254760154606231 |
| Trinity College | 51.75449619271991, -1.256710320873993 |
| Keble College | 51.759217321427734, -1.257168600436832 |
| Magdalen College | 51.75204251112559, -1.247512344710711 |
| Lincoln College | 51.75313221405275, -1.2560645073210122 |
| Brasenose | 51.75331532290772, -1.2543009131353227 |
References and more links
- [[Notes - ADS HT24, NP-hardness and NP-completeness]]U
- [[Notes - ADS HT24, Approximation algorithms]]U
- [[Notes - Models of Computation MT23, Turing machines]]U
- [[Quantum Computing Since Democritus, Aaronson]]N, Chapter 6, “$\mathbf P$, $\mathbf{NP}$ and Friends”
- “Travelling salesman problem” on Wikipedia
- “Christofides algorithm” on Wikipedia
- “Complexity class” on Wikipedia
