Wordsworth, a pencil-and-paper game

Created: October 08, 2024
Updated: November 02, 2024

The game

Wordsworth is a pencil-and-paper game between two players, also known by the names “Think of a Letter” or “Letterboxed” (not the NY Times game!). It works like this:

  • Setup: Both players draw a $5 \times 5$ grid that they keep hidden from one another.

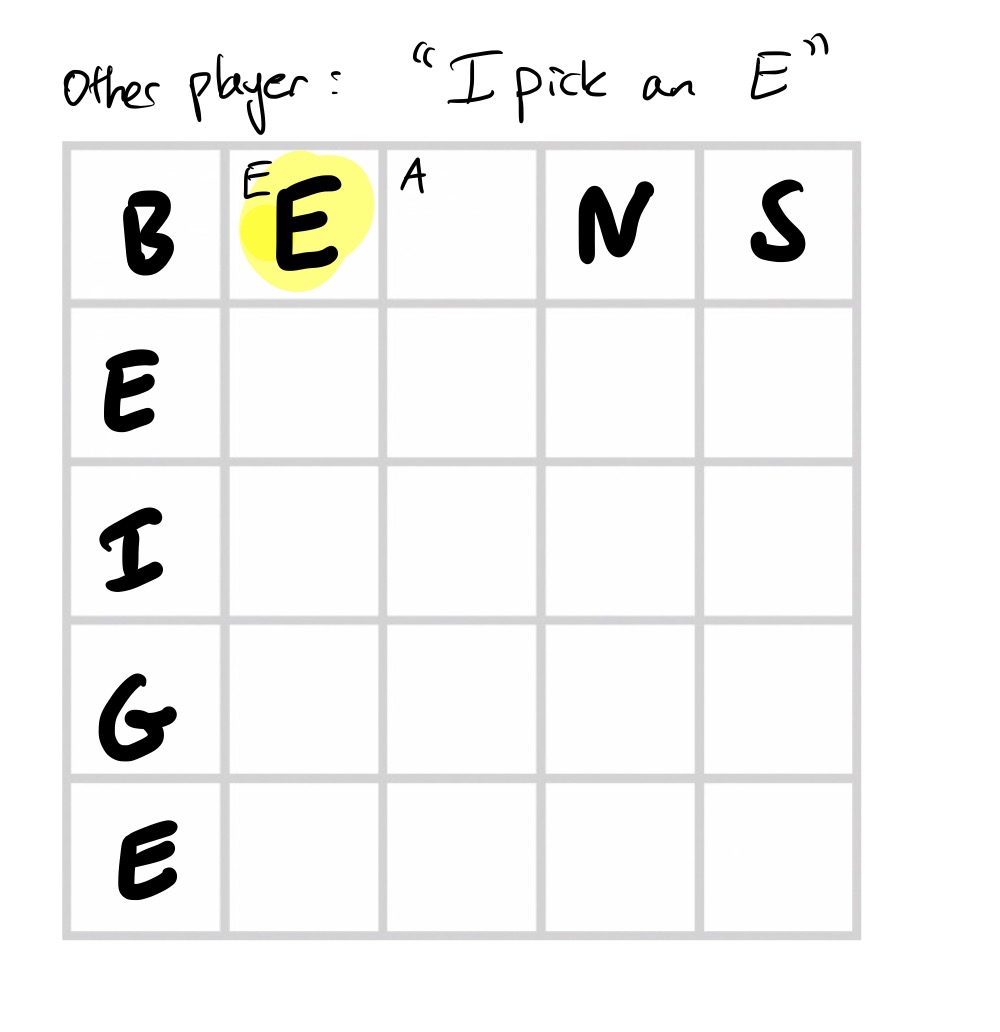
  • Play: The first player names a letter and writes it down in any of their unoccupied squares. The second player writes the letter play one has chosen in one of their unoccupied squares. Then it’s the second player’s turn to choose. They pick a letter and write it down in any of their unoccupied squares. Then the first player has to find somewhere to fit that letter. Play alternates like this, with one player choosing a letter and writing it down somewhere, with the other player having to find somewhere to put it, and the game is over when both grids are full.

  • Scoring: Each player examines each row or column of their grid separately. For each 5 letter word, they add 10 to their score. For each 4 letter word, they add 4 to their score. For each 3 letter word, they add 3 to their score. At most one word can be scored per row or column, and words on the diagonal do not count. The player with the highest score wins!


Here’s a snippet of an example game:

Opening

It’s our turn to go first: we start by calling out a “G” and placing it wherever we want in our grid:

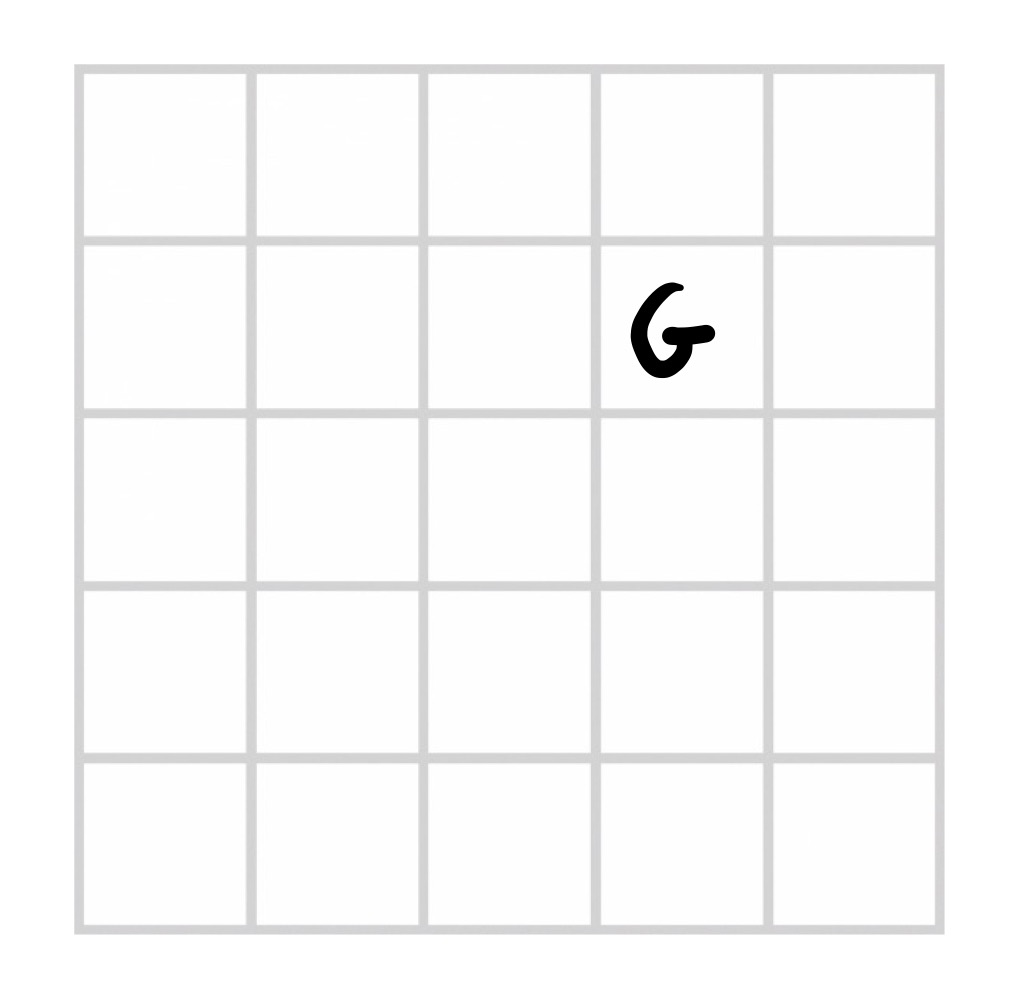
The opponent keeps where they’ve placed their “G” a secret. They then call out an “A”, which we have to find a place for:

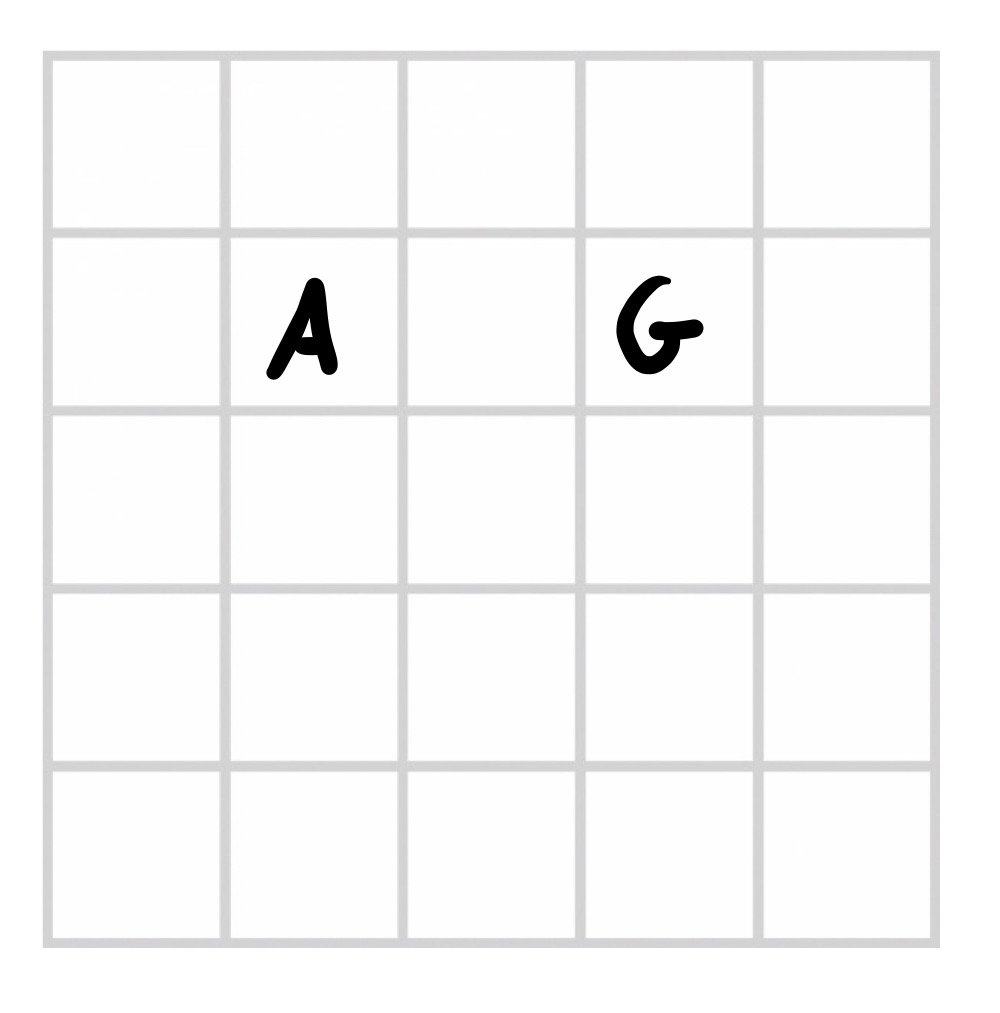
Midgame

…fast forward a few turns, now it’s our turn again and our grid is much fuller. We call out a “C” to turn “RAMS” into “CRAMS”:

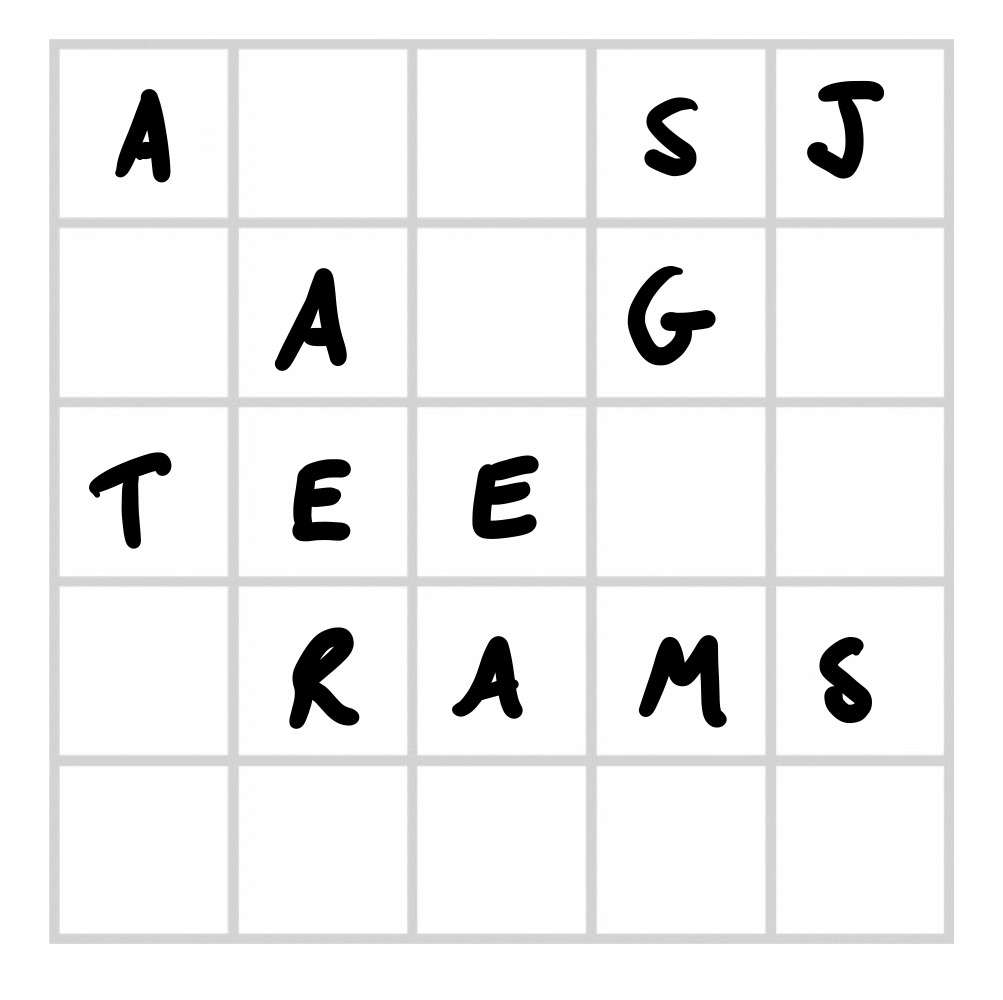
They then say “Y”, which we place somewhere we hope it won’t get in the way:

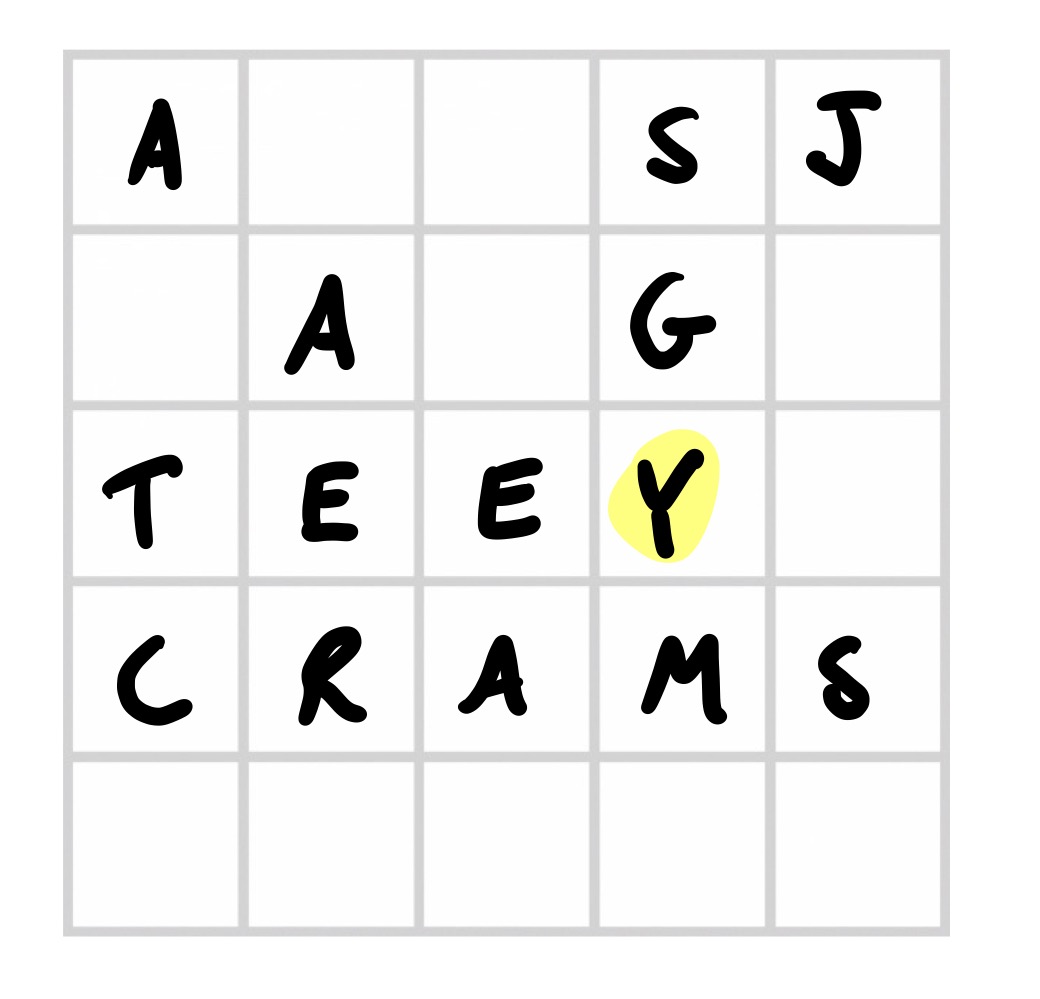
Endgame

…and after a few more turns, the game is over! This is our final grid, with the scores totalled up along the side and the bottom.

Getting a feel for the game

This game is great because it’s a more “word-y” alternative to other pencil and paper games like noughts and crosses or dots and boxes. Some mathematical games suffer being either too easy, and the winning strategy is obvious, or being too difficult, and it’s hard to make moves that don’t feel like random. This game fits into the healthy middle-ground, where you can tell that which moves are good or bad (don’t put “Z” everywhere), but thinking of the best move is a challenge (which letter could I pick which would give me the most options for words in the future?).

It is also an interesting game to analyse. Other famous pencil-and-paper games like Tic-Tac-Toe have been analysed to death: if you want some bedtime reading, there is a gigantic 750-page book called “Combinatorial Games: Tic-Tac-Toe Theory” which tries to answer some unsolved mathematical problems about the game.

But I can’t find much about this game online. So in an effort to change that, here’s some simple questions about the game, and (some of) the answers.

Some questions

Can you get the maximum score?

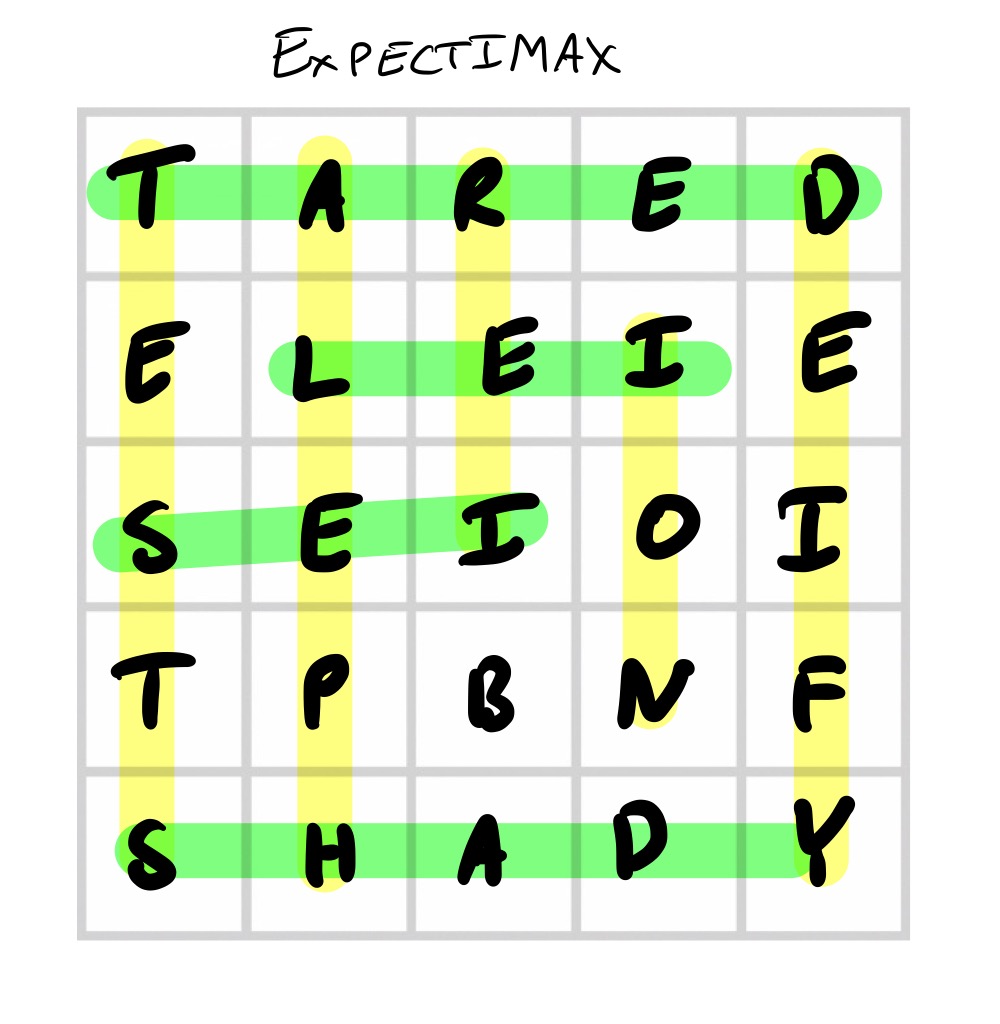
Yes! Firstly, what is the maximum score? Since you could feasibly have a 5-letter word in each of the 5 rows and the 5 columns, the best you could score would be 100. Searching for a configuration with the highest score is then same as finding grids of 5x5 letters where you can read words in every column and in every row. These have been studied before, and are called Word squares.

Here is one such grid:

To actually get this grid in a real game, you would have to be extremely lucky, since your opponent would have to give you half of the letters you need. I used a computer to find this with lots of number-crunching, but humans have actually been finding patterns like this by hand for at least a thousand years. This is the famous “Sator square”, which was found etched into a column in Pompeii:

It’s a little hard to make out, but the words are:

  • ROTAS: noun, wheels,
  • OPERA: noun, service, pains, labor; care, effort, attention,
  • TENET: verb, keeps, comprehends, possesses, masters,
  • AREPO: “unknown word, perhaps a proper name, either invented to complete the palindrome or of a non-Latin origin”,
  • SATOR: noun, sower, planter, founder, progenitor.

There’s debate around what the precise meaning and origin of this square is. But it’s time to put to rest centuries of academic research: it was just two ancient Romans playing Wordsworth.

Which 5-letter words are the most stable under edits?

By “stable under edits”, I mean that you can change one of the letters and still end up with a valid word. This is useful to know when actually playing the game because one strategy is to “plan out” certain words and slowly fill them in. When your opponent names one of the letters you’re about to write, it effectively saves you a turn since you can complete that word faster.

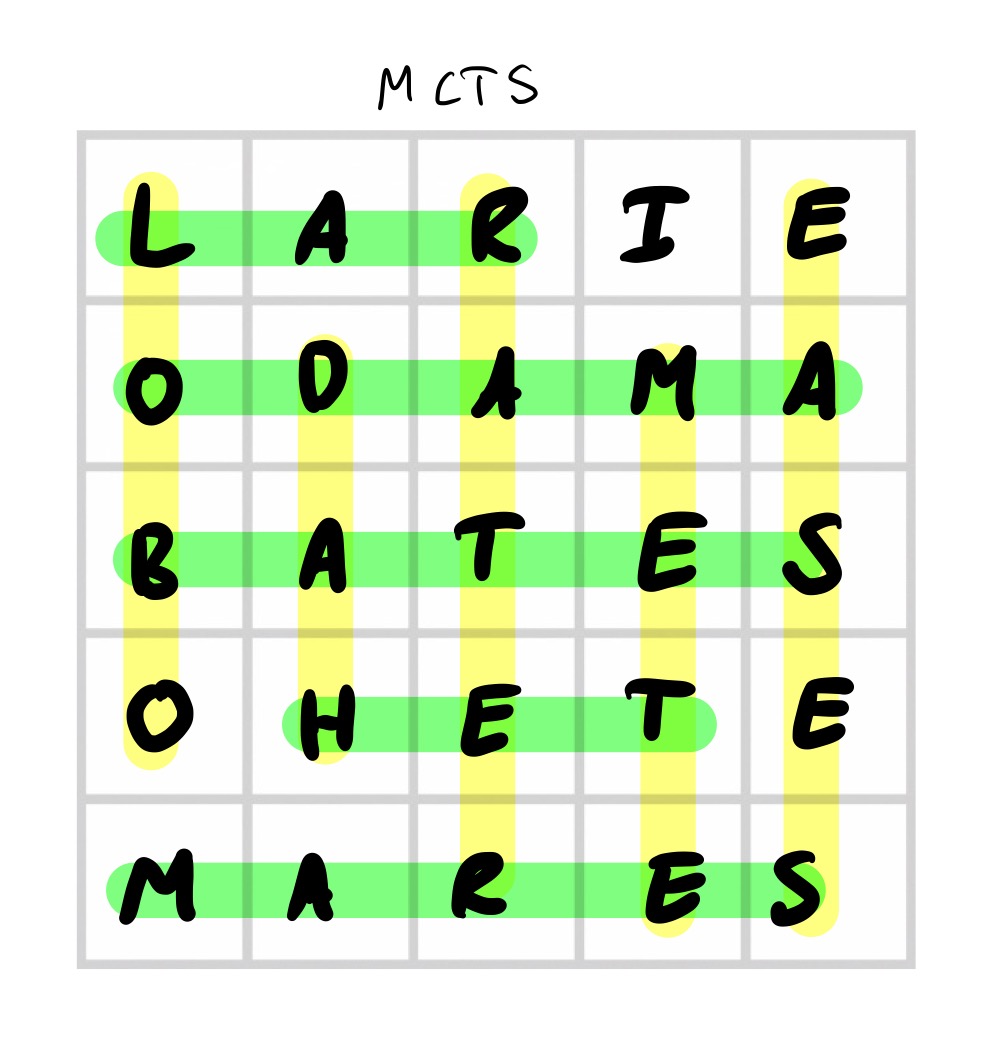
In the word list that I am using (Donald Knuth’s list of 5 letter words), the two most stable words are:

  • “cores”, can be changed into: bores, fores, gores, lores, mores, pores, sores, yores, cares, cures, codes, cokes, comes, cones, copes, cotes, coves, coxes, cords, corks, corms, corns, corps, cored, corer.
  • “bares”, can be changed into: bares, cares, dares, fares, hares, mares, nares, pares, tares, wares, bores, byres, babes, bakes, bales, banes, bases, bates, barbs, bards, barfs, barks, barms, barns, bared, barer.

This is good information to have when playing the game, but I think that the following word and its mutations may be more useful:

  • “sears”, can be changed into: bears, dears, fears, gears, hears, nears, pears, rears, sears, tears, wears, years, scars, soars, spars, stars, seers, seals, seams, seats.

This is because, despite there being less options, each of those words are more likely words in English if you were to pick random letters out of a distribution of English letters in dictionaries.

Computer strategies

This is an interesting game to write a computer program to play, since almost all examples online of simple game-playing computer programs focus on games where:

  • The players share the same board, and
  • The games are zero-sum (one player’s win is the other player’s loss).

Among these games are Tic-Tac-Toe, Checkers, Chess, Connect-4, and many more. For simple examples, most tutorials use the “minimax” algorithm with alpha-beta pruning.

Strictly considered, Wordsworth also has both of these characteristics. If you win, your opponent loses, and there is a sense in which you’re actually playing on one big board, but you can’t see your opponent’s side. But one reason that algorithms like minimax won’t do very well on Wordsworth is that the set of all possible games is so large. Since the player take turns picking one of the 26 letters in the alphabet 25 times independently, and each player can pick an arrangement of these letters, the total number of possible games is:

\[26^{25} \times (25!)^2 \approx 5.7 \times 10^{85}\]

The branching factor is much higher than that of chess and even Go, since each move increases the size of the search space by a factor of around $\sqrt[25]{5.7\times 10^{85}} \approx 2700$. For chess, the branch factor is roughly $30$, and for Go it is around $250$. Because of this, minimax won’t work very well: if the computer could analyse one position per nanosecond, it would take 5 years to think even 5 moves ahead.

So how can we tackle the size of the search space?

One way is to not model the opponent’s board. A game engine that considers all possibilities of what the opponent’s board looks like would be searching over the total number of games above, but you can cut this number down considerably by only modelling your board.

Modelling your opponent’s board does have its advantages, it means that the program can play adversarially – if it thought the opponent was waiting for more vowels, it could deliberately choose letters that they would struggle to fit. But in real play, the game feels a lot less adversarial than this: it’s more like you’re using the other player as a random letter generator and then comparing scores at the end.

If you don’t model the opponent’s board, then the number of possible games is:

\[25^{26} \times 25! \approx3.7 \times 10^{60}\]

and this gives an average branching factor of $270$, which is a lot more reasonable.

Using this simplification, Wordsworth instead becomes a one-player game with an element of chance; you could feasibly play by yourself against a 26-sided die. This means we can’t treat it as a zero-sum game, since now there is no opponent.

Here are some simple strategies based on these ideas.

Expectimax

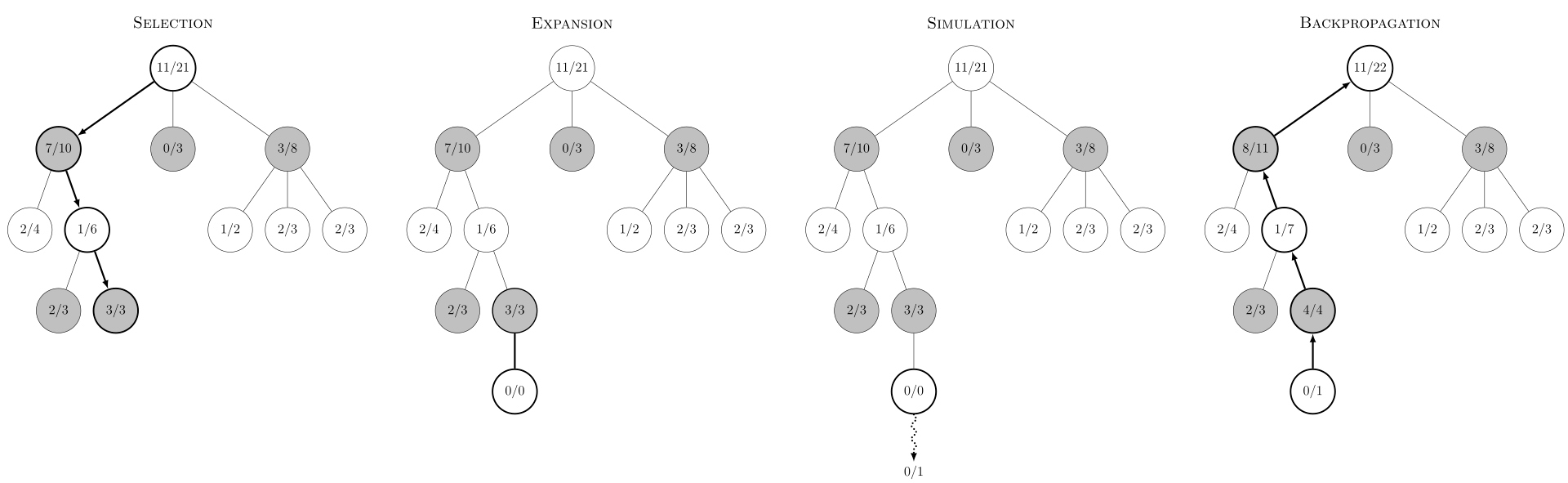
So minimax is out, because the game is not zero-sum. But there is a related algorithm called “expectimax” which deals with one-player games with chance.

Standard minimax works by considering the game tree and picking moves which will maximise the payoff, given an adversary who picks moves in order to minimise our payoff. Expectimax scraps the adversary, and instead replaces them with chance. It then picks the nodes with the highest expected value.

The branching factor is still way too large to get anywhere into the thicket of the game tree, so we also need a way of evaluating a partially completed position so that we can stop the search early rather than descending all the way in.

Say we’ve searched a few levels deep and now want to give the following position an evaluation:

One simple way of evaluating a position is to score contiguous words like normal, and ignore the blanks. Another way is to randomly complete the grid with random letters and then evaluate like normal.

Repeating this several times for different completions and then taking the average will give a better evaluation than the first method since it could account for words that need to just be filled by one letter.

Searching only a couple levels of the tree and evaluating positions like this gives a strategy that can score about 20 points on average when played against a player that picks randomly.

Monte-Carlo tree search (MCTS) is another strategy that can be used. I won’t explain it here in full, but MCTS is based on a similar idea to expectimax with a random evaluation function. Rather than exploring all nodes uniformly, it will instead treat the problem like a “multi-armed bandit problem” and only explore promising lines of play (see [[Algorithms to Live By, Christian]]N).

Monte-Carlo tree search was the basis behind the AlphaGo algorithm which became the first computer Go player to beat a human in a professional tournament.

Here are some other simple strategies to compare the above two strategies against.

Random

The idea behind this strategy is simple: if it’s your turn, pick a random letter and a random place for it, and if you’ve been given a letter you need to find a place for, pick a random position.

Sleepy

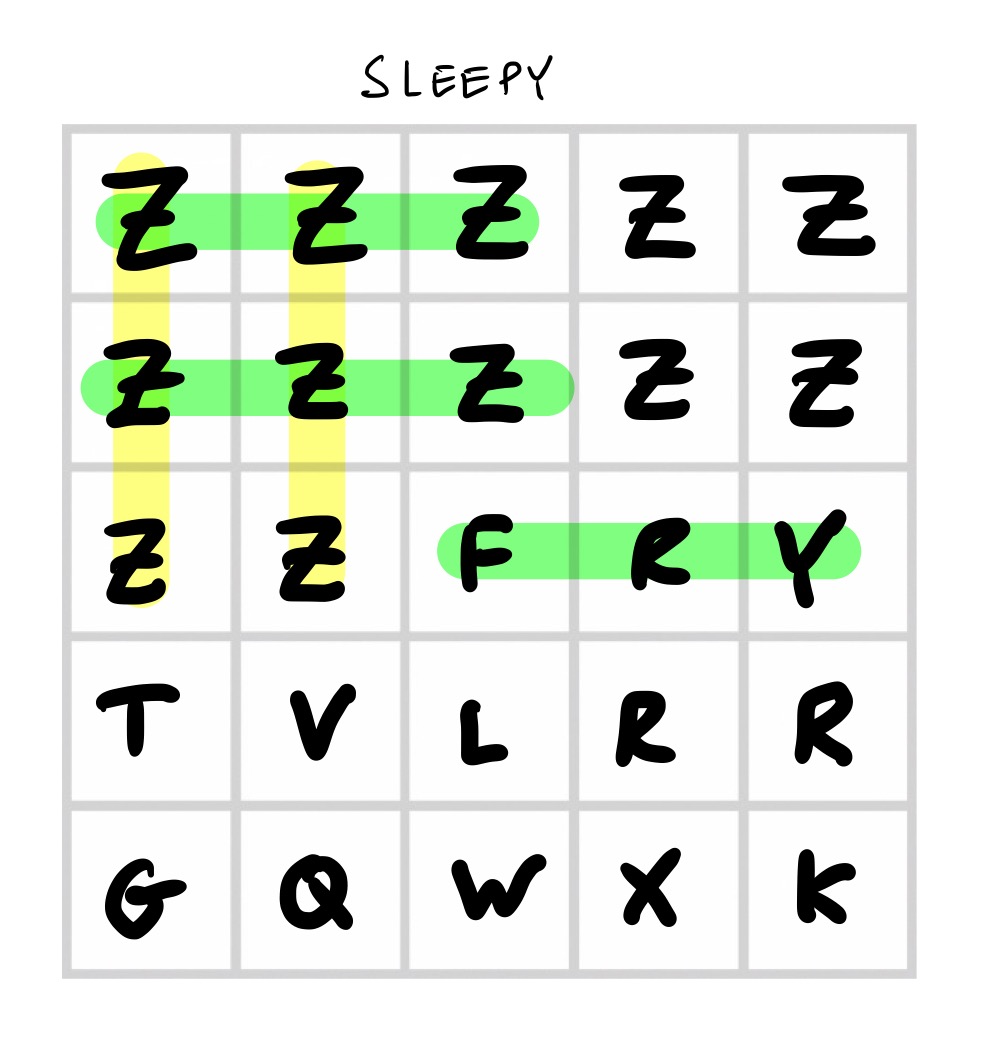
Just play as many “Z”s as possible, starting from the top of the grid and placing all your opponents letters at the end. Surprisingly, this does better than the fully random strategy! But only because according to the word list I am using, “ZZZ” is an English word.

EnglishRandom

This is almost identical to the random strategy, but rather than picking letters completely at random, this will pick letters biased towards their distribution in English. So it will pick an “E”s a lot more often than it will pick “Z”s.

ThinkRight

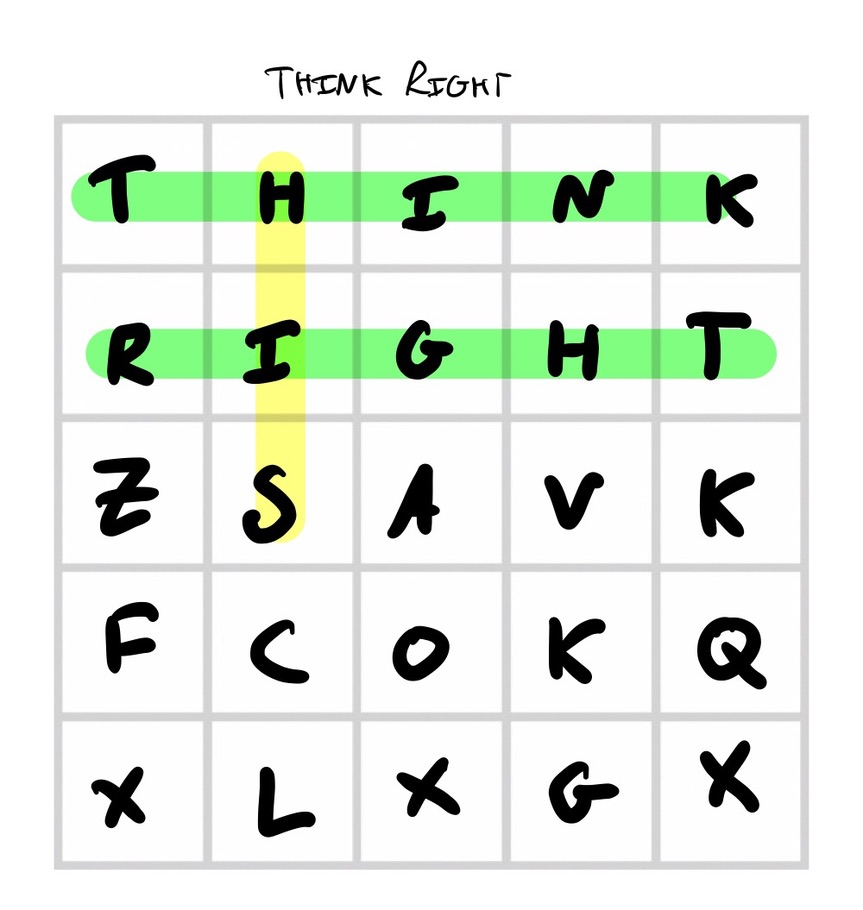
Use all your turns to play the words “THINK” and “RIGHT” at the top of the grid, placing your opponents letters at the bottom. This does

Results!

Let’s see which one is stronger by pitching them against one another in a tournament! Here are the overall results of between all the strategies, where they all play three rounds against one another:

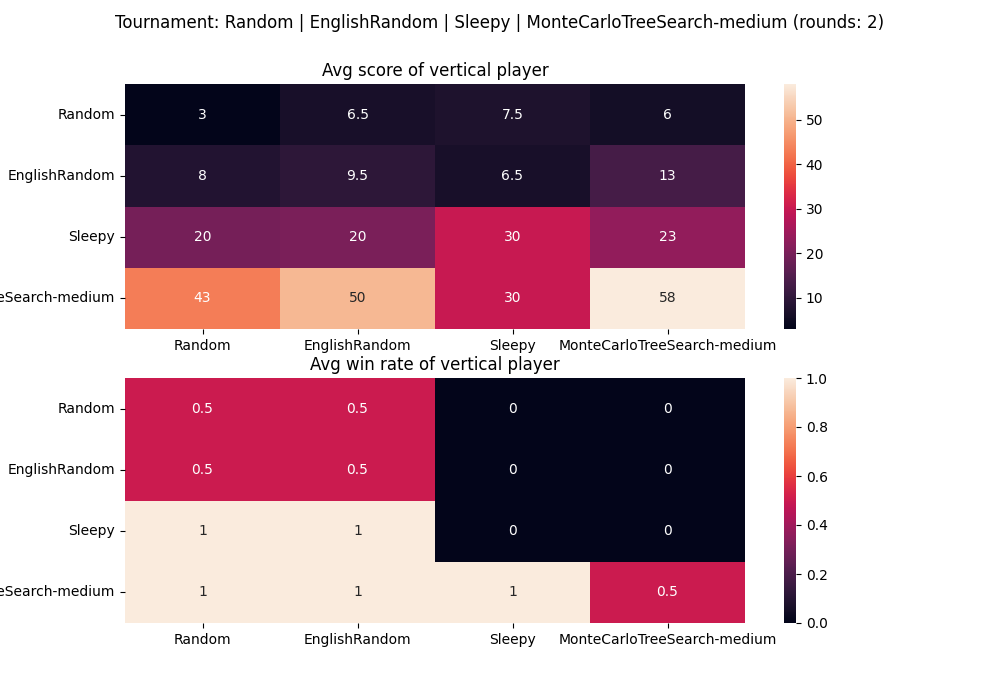
All the code for the strategies, analysis and generating tournament results is available on GitHub. If you have an idea for a better strategy, implement it and send a PR!

What about everything else?

The title “Almost everything to know about Wordsworth” is an exaggeration. There’s a million more questions which you could ask and I don’t have the answers to them here:

  • What other information would be useful in “real world” play?
    • “cares” and “bares” are the most stable words under simple edits, but which words have the most neighbours when there are one or two letter changes?
  • If you play a “fixed strategy” like “Sleepy” or “ThinkRight” above, which set of letters and positions do the best on average? This would also be useful information in real world play.
  • Other compute strategies:
    • Expectimax does no pruning, how can you more effectively reduce the size of the search space?
    • Implement in OpenSpeil and use better algorithms cooked up by Google Deepmind researchers?
    • The Monte-Carlo and Expectimax strategies probably aren’t very smart in the opening since they can’t see far enough in the future. Write better evaluation functions based on game phases?
    • Implement parallelisation for the Monte-Carlo algorithm?
  • What happens if you change
  • What other interesting variants can you consider?
    • Is there a way of making the game feel more adversarial, rather than it feeling like your opponent is just a random letter generator?


Related posts