Flashcards
What is the STRIPS language.
A logical language for encoding planning problems.
@Define a first-order atom.
where
- $P$ is a predicate, e.g. $\text{Raining}$ or $\text{IsBrother}$
- $t _ i$ are terms: variables, constants or function terms.
Intuitively, what is a constant in first-order logic?
The representation of some object.
Intuitively, what is a predicate in first-order logic?
A $n$-ary relation between objects.
@Define formally a function term in first-order logic and then give an intuitive explanation.
\[f(t_1, \ldots, t_n)\]
where
- $t _ i$ are terms: variables, constants or function terms.
Intuitively, they represent a function from some objects to another object.
@Define a literal in first-order logic.
A positive or negative atom.
@Define ground atoms and ground literals in first-order logic.
Atoms and literals that do not contain variables.
@Define the components of a planning problem when formulated in the STRIPS language.
- Predicates: A set of possible predicates (relations) used in formulating the problem.
- Constants: A set of constants (objects) used in formulating the problem.
- States: A set of positive ground atoms describing what holds currently, in terms of these predicates and constants
- e.g. $\{\text{At}(\textit{Home}), \text{Have}(\textit{Milk})\}$
- Initial state
- Goal: A set of ground atoms to be made true (also allowed a superset):
- e.g. $\{\text{At}(\textit{Home}), \text{Have}(\textit{Drill})\}$.
- Action: A precondition and postcondition
- Precondition: What must be true before an action is carried out
- Postcondition: A set of atoms to be added (appear positively) and a set of atoms to be removed (appear negatively)
Give an @example STRIPS action which describes buying a drill from a hardware store.
- Action: $\text{Buy}(\textit{Drill})$
- Precondition: $\text{At}(\textit{HardwareStore})$, $\text{Sells}(\textit{HardwareStore, Drill})$.
- Postcondition: $\lnot \text{Sells}(\textit{HardwareStore, Drill})$, $\text{Have}(\textit{Drill})$
In STRIPS, it is possible to define actions in terms of variables like so:
- Action: $\text{Buy}(\textit{x})$
- Precondition: $\text{At}(\textit{p})$, $\text{Sells}(\textit{x, p})$.
- Postcondition: $\lnot \text{Sells}(\textit{p, x})$, $\text{Have}(\textit{x})$
What is the problem with this as it stands, and how can you overcome this problem?
$x$ might not be an object and $p$ might not be a place. In order to fix this, you need to add new atoms which effectively “type” the variables:
- Action: $\text{Buy}(\textit{x})$
- Precondition: $\text{At}(\textit{p})$, $\text{Sells}(\textit{x, p})$, $\text{IsPlace}(p)$, $\text{IsObject}(x)$.
- Postcondition: $\lnot \text{Sells}(\textit{p, x})$, $\text{Have}(\textit{x})$
What is the difference between PDDL and STRIPS?
STRIPS does not allow negative literals in preconditions of actions, whereas PDDL does.
Describe the basics of the backward (regression) planning @algorithm.
- Start with a goal state $G$
- Pick an action $A$ that is:
- Relevant: achieves literal in $G$, so contains a literal $B$ such that $B$ is in $G$
- Consistent: doesn’t undo a literal in $G$, so the postcondition doesn’t contain a literal $\lnot B$ such that $B$ is in $G$
- For simplicity, consider actions where variables occuring in the postcondition of the action also occur in the precondition (otherwise searching gets complicated)
- Compute the predecessor state
- Use $A^\ast$ to do this repeatedly until the initial state is reached
Why isn’t forward search used in STRIPS?
Because there is a high branching factor and you can end up picking lots of irrelevant actions.
What are 4 main heuristics that can be used when using $A^\ast$ and STRIPS?
- Ignore preconditions
- Every action becomes applicable in every state
- Ignore negative effects
- No action can remove an atom from the current state
- State abstraction
- Remove all atoms over some predicate in pre- and post-conditions
- Subgoal independence
- Split all goal atoms into disjoint subsets, and consider min-cost plans to solve the subsets
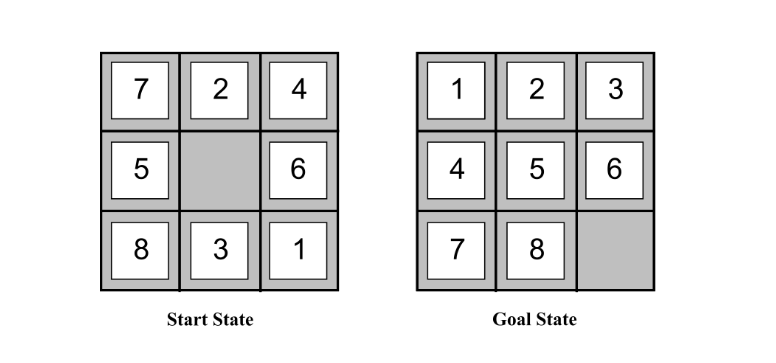
Consider the STRIPS formulation of the action of sliding tile $t$ from position $a$ to position $b$:
- Action: $\text{Slide}(t, a, b)$
- Precondition: $\text{Tile}(t)$, $\text{On}(t, a)$, $\text{Adjacent}(a, b)$, $\text{Empty}(b)$
- Effect: $\text{On}(t, b)$, $\text{Empty}(a)$, $\lnot \text{On}(t, a)$, $\lnot \text{Empty}(b)$
When solving planning problems like this with $A^\ast$, it’s useful to have a good heuristic. One general purpose planning heuristic is ignoring preconditions. Can you explain this, give the “updated” action definition, and describe the intuitive 8 puzzle-specific heuristic this leads to?

Remove all preconditions so that every action in available in every state. This leads to the new action:
- Action: $\text{Slide}(t, a, b)$
- Precondition: …
- Effect: $\text{On}(t, b)$, $\text{Empty}(a)$, $\lnot \text{On}(t, a)$, $\lnot \text{Empty}(b)$
and an optimal solution to this planning problem corresponds to the “number of tiles out of place” heuristic.
(also, this relaxed problem is at least as hard as the $\mathbf{NP}$-hard $\mathbf{SetCover}$ problem, since you’re picking the least number of actions to cover all atoms in the goal, but this could be seen as a good thing as $\mathbf{SetCover}$ has efficient approximation algorithms).

Consider the STRIPS formulation of the action of sliding tile $t$ from position $a$ to position $b$:
- Action: $\text{Slide}(t, a, b)$
- Precondition: $\text{Tile}(t)$, $\text{On}(t, a)$, $\text{Adjacent}(a, b)$, $\text{Empty}(b)$
- Effect: $\text{On}(t, b)$, $\text{Empty}(a)$, $\lnot \text{On}(t, a)$, $\lnot \text{Empty}(b)$
When solving planning problems like this with $A^\ast$, it’s useful to have a good heuristic. One general purpose planning heuristic is ignoring negative effects. Can you explain this and give the “updated” action definition?

Remove all negative atoms from the effect/postcondition. This leads to:
- Action: $\text{Slide}(t, a, b)$
- Precondition: $\text{Tile}(t)$, $\text{On}(t, a)$, $\text{Adjacent}(a, b)$, $\text{Empty}(b)$
- Effect: $\text{On}(t, b)$, $\text{Empty}(a)$

Consider the STRIPS formulation of the action of sliding tile $t$ from position $a$ to position $b$:
- Action: $\text{Slide}(t, a, b)$
- Precondition: $\text{Tile}(t)$, $\text{On}(t, a)$, $\text{Adjacent}(a, b)$, $\text{Empty}(b)$
- Effect: $\text{On}(t, b)$, $\text{Empty}(a)$, $\lnot \text{On}(t, a)$, $\lnot \text{Empty}(b)$
When solving planning problems like this with $A^\ast$, it’s useful to have a good heuristic. One general purpose planning heuristic is state abstraction. Can you explain this, give the “updated” action definition when considering the $\text{Empty}$ predicate, and explain the intuitive 8-puzzle heuristic this leads to?

Drop all atoms over some predicate. In the case of the $\text{Empty}$ predicate, this is
- Action: $\text{Slide}(t, a, b)$
- Precondition: $\text{Tile}(t)$, $\text{On}(t, a)$, $\text{Adjacent}(a, b)$
- Effect: $\text{On}(t, b)$, $\lnot \text{On}(t, a)$
The optimal solution to this relaxed problem corresponds to the Manhattan distance heuristic.

Consider the STRIPS formulation of the 8 puzzle.
When solving planning problems like this with $A^\ast$, it’s useful to have a good heuristic. One general purpose planning heuristic is subgoal independence. Can you explain this in detail?

- Let $G _ 1, \ldots, G _ n$ be disjoint subsets of goal atoms.
- Let $P _ 1, \ldots, P _ n$ be min-cost plans that achieve $G _ 1, \ldots, G _ n$
Then take as heuristic
\[\max_i \text{Cost}(P_i)\]
Consider the STRIPS formulation of the 8 puzzle.
When solving planning problems like this with $A^\ast$, it’s useful to have a good heuristic. One general purpose planning heuristic is subgoal independence. This involves considering:
- Let $G _ 1, \ldots, G _ n$ be disjoint subsets of goal atoms.
- Let $P _ 1, \ldots, P _ n$ be min-cost plans that achieve $G _ 1, \ldots, G _ n$
and then taking as a heuristic
\[\max_i \text{Cost}(P_i)\]
Sometimes it’s possible to do better than this using independent subproblems. Can you describe this?

Instead take as heuristic
\[\sum^n_{i = 1} \text{Cost}(P_i)\]This is possible when the plans $P _ i$ and $P _ j$ are independent, i.e. the effects of actions in $P _ i$ leave the preconditions and effects of all actions in $P _ j$ unchanged.