Further Maths - Cross Product

Created: January 25, 2022
Updated: August 24, 2024

Flashcards

2022-01-25

What is the cross product useful for?

Finding a normal vector to two other vectors.

What is another name for the cross product?

The vector product.

Does the cross product give you a scalar or a vector answer?

A vector.

How can you work out the direction of the cross product of two vectors?

Using the right hand rule.

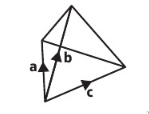
In the right hand rule for working out the direction of the cross product, what is the first vector $a$ represented by?

Your first finger.

In the right hand rule for working out the direction of the cross product, what is the second vector $b$ represented by?

Your second finger.

In the right hand rule for working out the direction of the cross product, what is the resulting normal vector represented by?

Your thumb.

Can you demonstrate the right-hand rule by wiggling each finger in turn for $a$, $b$ and $\hat{n}$?
  • $a$ is first finger
  • $b$ is second finger
  • $\hat{n}$ is third finger

Is the vector/cross product commutative?

No.

What is $\pmb{i} \times \pmb{i}$?
\[\pmb{0}\]

What is $\pmb{j} \times \pmb{j}$?
\[\pmb{0}\]

What is $\pmb{k} \times \pmb{k}$?
\[\pmb{0}\]

What is $\pmb{i} \times \pmb{j}$?
\[\pmb{k}\]

What is $\pmb{j} \times \pmb{i}$?
\[\pmb{-k}\]

What is $\pmb{j} \times \pmb{k}$?
\[\pmb{i}\]

What is $\pmb{k} \times \pmb{j}$?
\[\pmb{-i}\]

What is $\pmb{k} \times \pmb{i}$?
\[\pmb{j}\]

What is $\pmb{i} \times \pmb{k}$?
\[\pmb{-j}\]

What’s the nice way of remembering the cross product rules for unit vectors?
  • If there are two successive different unit vectors, it’s the positive final one.
  • If they aren’t in order, then it’s the negative final one.

What’s the actual mathematical definition of the cross product in terms of $a$, $b$ and $\theta$?
\[a \times b = |a||b| \sin \theta \hat{n}\]

What is

\[b \times a\]

equivalent to (cross product)?
\[-a \times b\]

What does it mean for the cross product of two vectors to be $0$?

Either at least one of them is $\pmb{0}$ or they are parallel.

How can you use the cross product to work out if two vectors are parallel?

See if it equals $\pmb{0}$.

What’s the cross product of two vectors

\[\left(\begin{matrix} a _ 1 \\ a _ 2 \\ a _ 3 \end{matrix}\right) \times \left(\begin{matrix} b _ 1 \\ b _ 2 \\ b _ 3 \end{matrix}\right)\]

in terms of the determinant of a matrix?
\[\left|\begin{matrix} \pmb{i} & \pmb{j} & \pmb{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{matrix}\right|\]

To work out the unit normal vector using the cross product, what must you remember to do by the end?

Divide by the magnitude.

What is $\sin \theta$ in terms of $a$ and $b$ using the cross product?
\[\sin \theta = \frac{|a \times b|}{|a||b|}\]

How could you prove that if

\[a + b + c = 0\]

then

\[a \times b = b \times c = c \times a\]

(where $a$, $b$ and $c$ are vectors)?

Multiply the original equation by $a$ and then $b$.

What’s $a \times (b + c)$ (cross product)?
\[a\times b + a\times c\]

The cross product isn’t commutative, but it is gosh-darn rootin’-tootin’ what?

Distributive.

2022-01-26

Why can you take the absolute value of both sides of $a \times b = \vert a \vert \vert b \vert \sin\theta \hat{n}$ to get $ \vert a \times b \vert = \vert a \vert \vert b \vert \sin\theta$?

Because $ \vert \hat{n} \vert = 1$

If $ \vert a \times b \vert = \vert a \vert \vert b \vert \sin\theta$ and the area of a triangle is $\frac{1}{2} ab$, then how could you think about $ \vert a \times b \vert $?

As double the area of a triangle.

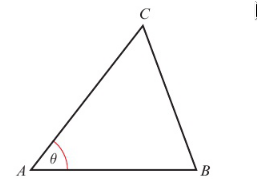PHOTO TRIANGLE AREA What is the area of this shape in terms of the cross product?
\[\frac{1}{2} ((c - a) \times (b - a))\]

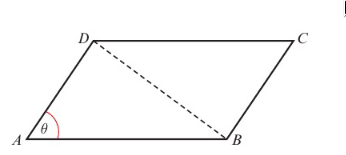PHOTO PARALLELOGRAM AREA What is the area of this shape in terms of the cross product?
\[(d - a) \times (b - a)\]

What is the scalar triple product for $a$, $b$ and $c$ in terms of the cross product?
\[a \cdot (b \times c)\]

What is the scalar triple product for $a$, $b$ and $c$ as the determinant of a matrix?
\[\left|\begin{matrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{matrix}\right|\]

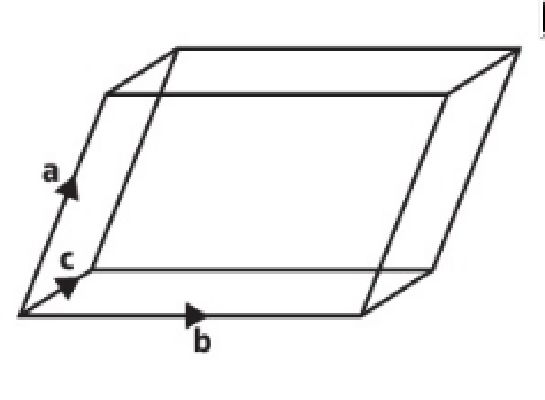PHOTO PARALLELEPIPED AREA What is the name of this shape?

A parallelepiped.

What is the mathematical definition of a parallelepiped?

A 3D shape formed by six parallelograms.

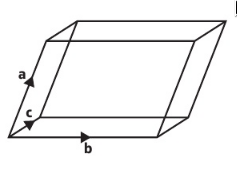PHOTO PARALLELEPIPED AREA What is the formula for the volume of this shape?
\[|a \cdot (b \times c)|\]

What important property does the scalar triple product have that makes it easier to use?

It is cyclic.

If

\[\pmb{a} \cdot (\pmb{b} \times \pmb{c}) = d\]

then what does

\[\pmb{b} \cdot (\pmb{c} \times \pmb{a})\]

equal?
\[d\]

If any of the terms in

\[\pmb{a} \cdot (\pmb{b} \times \pmb{c})\]

are equal, then what must the result be?
\[0\]

Does the scalar triple product give a vector or a scalar answer?

A scalar.

PHOTO TETRAHEDRON VOLUME What is the name of this shape?

A tetrahedron.

PHOTO TETRAHEDRON VOLUME What is the formula for the volume of this shape?
\[\frac{1}{6} | a \cdot (b \times c) |\]

When using the cross product or scalar triple product to work out volumes, what is important?

That you use direction vectors from a single point, not arbitrary position vectors.

How would you prove a shape described with vectors is regular?

Show that all the edge lengths are the same.

2022-01-27

Straight Lines

What is the cross product form of a straight line $r = a + \lambda b$?
\[(r - a) \times b = 0\]

Why is the cross product form of a straight line useful?

Because it means you don’t have to have a parameter.

What is another form for the straight line equation $(r - a) \times b = 0$?
\[r \times b = a \times b\]

What’s the geometric interpretation of the cross product straight line formula $(r - a) \times b = 0$?

$r - a$ is the direction vector between a general point and any point on the line, so you’re saying that it has to be parallel to the direction vector.

For a direction vector

\[a = \left(\begin{matrix} x \\ y \\ z \end{matrix}\right)\]

how can you work out the angle it makes with the $y$-axis?
\[\cos \theta = \frac{y}{|a|}\]

For a direction vector

\[a = \left(\begin{matrix} x \\ y \\ z \end{matrix}\right)\]

how can you work out the angle it makes with the $x$-axis?
\[\cos \theta = \frac{x}{|a|}\]

For a direction vector

\[a = \left(\begin{matrix} x \\ y \\ z \end{matrix}\right)\]

how can you work out the angle it makes with the $z$-axis?
\[\cos \theta = \frac{z}{|a|}\]

What letters are used for the direction cosines of a vector $\frac{x}{ \vert a \vert }$, $\frac{y}{ \vert a \vert }$ and $\frac{z}{ \vert a \vert }$?
\[l, m, n\]

What is true about the sum of the squares of direction cosines $\frac{x}{ \vert a \vert }^2$, $\frac{y}{ \vert a \vert }^2$ and $\frac{z}{ \vert a \vert }^2$?

They always sum to one.

For a vector

\[a = \left(\begin{matrix} x \\ y \\ z \end{matrix}\right)\]

how could you write the unit vector in terms of the direction cosines $\cos \alpha$, $\cos \beta$ and $\cos \gamma$?
\[\left(\begin{matrix} \cos \alpha \\\\ \cos \beta \\\\ \cos \gamma \end{matrix}\right)\]

How does the cross product make finding the vector equation for a plane easier?

Because it can give you the normal vector to two direction vectors.

\[r = a + \lambda b + \mu c\]

What is the dot product form of this plane equation using the cross product?
\[r \cdot (b \times c) = a \cdot (b \times c)\]

How can you use the cross product to find the line of intersection between two planes?

Find the vector perpendicular to the two normal vectors and then use the “let $z = 0$” approach to finding the point of intersection.

If you’ve got the direction vector of the line of intersection between two planes, how can you find a point that the line goes through given the two plane equations?

Assume that $z = 0$ and find the corresponding $x$ and $y$ values using the two simultaneous equations.

\[x + 2y + 3z = 4 \\ 3x + y + 4z = 1\]

You’ve already found the direction vector for the line of intersection of two planes. How can you now find a point on the plane?

Let $z = 0$ and then solve the equations simultaneously:

\[x + 2y = 4 \\\\ 3x + y = 1\]

What is the formula for the shortest distance between skew lines

\[r = a + \lambda b \\ r = c + \mu d\]

?
\[\left| (a - c) \cdot \frac{b \cross d}{|b \times d|} \right|\]

How could you remember the formula for the shortest distance between two skew lines

\[r = a + \lambda b \\ r = c + \mu d\]

as a sentence?

It’s the vector moving between the two known points ($a - c$) dot producted with the unit vector perpendicular to both direction vectors ($\frac{b\cross d}{ \vert b \cross d \vert }$)

2022-04-18

\[\left( \pmb{r} - \left(\begin{matrix} 2 \\ -1 \\ 2 \end{matrix}\right) \right) \times \left(\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}\right) = \pmb{0}\]

Why do you need to be careful expanding this?

The order of the cross product must be correct otherwise you’ll get a negative answer.



Related posts