Further Maths - Hyperbolic Functions

Created: March 15, 2021

See Also

Flashcards

2021-03-15

\[\sinh x\]

What is the definition?
\[\frac{e^x - e^{-x}}{2}\]
\[\cosh x\]

What is the definition?
\[\frac{e^x + e^{-x}}{2}\]
\[\tanh x\]

What is the definition?
\[\frac{e^{2x} - 1}{e^{2x} + 1}\]

PHOTO SINH GRAPH What function is this?
\[\sinh\]

PHOTO COSH GRAPH What function is this?
\[\cosh\]

PHOTO TANH GRAPH What function is this?
\[\tanh\]
\[y = \sinh x\]

What does the graph look like?

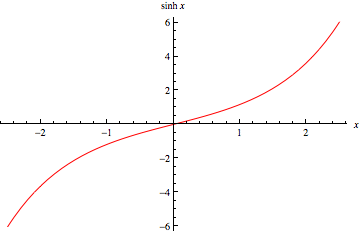
PHOTO SINH GRAPH

\[y = \cosh x\]

What does the graph look like?

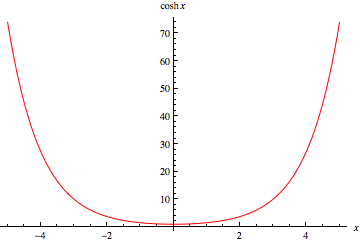
PHOTO COSH GRAPH

\[y = \tanh x\]

What does the graph look like?

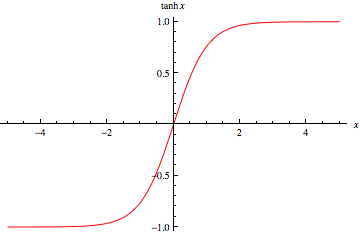
PHOTO TANH GRAPH

What is true about any value of $\cosh x$?

It is above $1$.

\[e^x - e^{-x} = 10\]

How would you rewrite this?
\[e^2x - 1 = 10e^x\]

2021-03-16

\[\arcsinh x\]

What is the definition?
\[\ln(x + \sqrt{x^2 + 1})\]
\[\arcosh x\]

What is the definition?
\[\ln(x + \sqrt{x^2 - 1})\]
\[\artanh x\]

What is the definition?
\[\frac{1}{2}\ln\left(\frac{1 + x}{1 - x}\right)\]

What is the domain for $\arcosh x$?
\[x \ge 1\]

What is the domain for $\artanh x$??

\[|x| < 1\]

PHOTO ARSINH GRAPH What function is this?
\[\arsinh\]

PHOTO ARCOSH GRAPH What function is this?
\[\arcosh\]

PHOTO ARTANH GRAPH What function is this?
\[\artanh\]
\[y = \arsinh x\]

What does the graph look like?

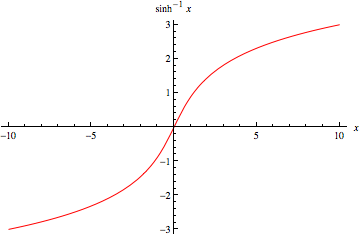
PHOTO ARSINH GRAPH

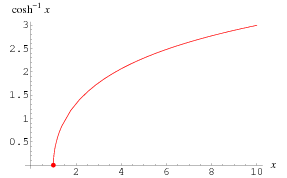
\[y = \arcosh x\]

What does the graph look like?

PHOTO ARCOSH GRAPH

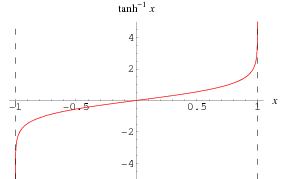
\[y = \artanh x\]

What does the graph look like?

PHOTO ARTANH GRAPH

What is true about any value of $\cosh x$?

It is above $1$.

2021-03-17

What is Osborn’s Rule?

Replace any product of two $\sin$ terms by minus the products of two $\sin$ terms.

By Osborn’s Rule, what is $\sinA\sinB$ in hyperbolic functions?
\[-\sinhA\sinhB\]

By Osborn’s Rule, what is $\tan^2 x$ in hyperbolic functions?
\[-\tanh^2 x\]

How do you convert a trig identity to a hyperbolic trig identity?
  • Replace all normal functions with their hyperbolic equivalents
  • Use Osborn’s Rule

If you’re not allowed to use Osborn’s Rule when converting a hyperbolic trig identity, what can you do?

Use the $e^x$ defintitions of all the functions.

\[\sin^2 x + \cos^2 x = 1\]

What is the hyperbolic equivalent?
\[\cos^2 x - \sin^2 x = 1\]
\[\frac{d}{dx} \sinh x\]

What is this equal to?
\[\cosh x\]
\[\frac{d}{dx} \cosh x\]

What is this equal to?
\[\sinh x\]
\[\frac{d}{dx} \tanh x\]

What is this equal to?
\[\sech^2 x\]
\[\frac{d}{dx} (\sinh^{-1} x)\]

What is the equal to?
\[\frac{1}{\frac{x^2 + 1}}\]
\[\frac{d}{dx} (\cosh^{-1} x)\]

What is the equal to?
\[\frac{1}{\frac{x^2 - 1}}\]
\[\frac{d}{dx} (\tanh^{-1} x)\]

What is the equal to?
\[\frac{1}{\frac{1 - x^2}}\]

2021-03-24

If $y = \sinh^{-1}(x)$, what is $x$ equal to?
\[x = \sinh(y)\]
\[x = \sinh(y)\]

What do you get if you differentiate both sides?
\[\frac{dx}{dy} = \cosh(y)\]
\[\frac{dx}{dy} = \cosh(y)\]

The aim here is to get $\frac{dy}{dx}$. How could you write $\cosh(y)$ made out of something you already know?
\[\frac{dx}{dy} = \sqrt{1 + \sinh^2(y)}\]
\[\frac{dx}{dx} = \sqrt{1 + \sinh^2(x)}\]

How could you rewrite this in terms of what you already know?
\[\frac{dx}{dy} = \sqrt{1 + x^2]}\]
\[\frac{dx}{dy} = u\]

How could you rewrite this so it’s $\frac{dy}{dx}$?
\[\frac{dy}{dx} = \frac{1}{\sqrt{1 + x^2}}\]

When finding the derivative of an inverse function, what’s the trick?

Rewriting some $f(y)$ in terms of $x$.

2021-03-25

\[\int \frac{1}{\sqrt{x^2 + 1}}dx\]

What is this equal to?
\[\sinh^{-1} x\]
\[\int \frac{1}{\sqrt{x^2 - 1}}dx\]

What is this equal to?
\[\cosh^{-1} x\]
\[\frac{d}{dx}\left(\sinh^{-1}\left(\frac{x}{a}\right)\right)\]

What is this equal to?
\[\frac{1}{\sqrt{x^2 + a^2}}\]
\[\frac{d}{dx}\left(\cosh^{-1}\left(\frac{x}{a}\right)\right)\]

What is this equal to?
\[\frac{1}{\sqrt{x^2 - a^2}}\]
\[\int\frac{1}{\sqrt{x^2 + a^2}}dx\]

What is this equal to?
\[\sinh^{-1}\left(\frac{x}{a}\right) \pmb{+ c}\]
\[\int\frac{1}{\sqrt{x^2 - a^2}}dx\]

What is this equal to?
\[\cosh^{-1}\left(\frac{x}{a}\right) \pmb{+ c}\]
\[\int\frac{1}{\sqrt{x^2 - 16}}dx\]

What is this equal to?
\[\cosh^{-1}\left(\frac{x}{4}\right) \pmb{+ c}\]
\[\int\frac{1}{\sqrt{x^2 + 8}}dx\]

What is this equal to?
\[\sinh^{-1}\left(\frac{x}{2\sqrt{2}}\right) \pmb{+ c}\]
\[\sqrt{4x^2 + 1}\]

How could you rewrite this to aid with integrating?
\[2\sqrt{x^2 + \frac{1}{2}}\]


Related posts