Further Maths - Polar Form

What is the name for $ \vert z \vert $?

The modulus of $z$.

What is the value of $ \vert z \vert $, where $z = a + bi$?

\[\sqrt{a^2 + b^2}\]

What is the value of $ \vert z \vert ^2$, where $z = a + bi$?

\[a^2 + b^2\]

If $ \vert z \vert ^2 = a^2 + b^2$, how could you also write $ \vert z \vert ^2$?

\[(a + bi)(a - bi)\]

What is the word definition of the modulus of $z$?

The distance to $z$ from the origin.

What is the name for $\text{arg} z$?

The argument of $z$.

What is the word definition of the argument of $z$?

The angle that a line drawn to $z$ makes with the real axis, in the anticlockwise

What is the range of the argument $\theta$ of a complex number?

\[-\pi < \theta \le \pi\]

What typically are the units of $\text{arg} z$?

Radians.

What is the principal argument?

The argument of $z$ in the range $-\pi < \theta \le \pi$.

Assuming all points are some horizontal distance $a$ away from the origin and a vertical distance $b$ in 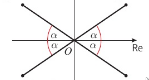, how could you write the angle they make with the real axis?

\[\tan^{-1}\left(\frac{b}{a}\right)\]

In , what is the formula in terms of $\alpha$ for the argument of $z$ for the first quadrant?

\[\text{arg}z = \alpha\]

In , what is the formula in terms of $\alpha$ for the argument of $z$ for the second quadrant?

\[\text{arg}z = \pi-\alpha\]

In , what is the formula in terms of $\alpha$ for the argument of $z$ for the third quadrant?

\[\text{arg}z = -(\pi-\alpha)\]

In , what is the formula in terms of $\alpha$ for the argument of $z$ for the fourth quadrant?

\[\text{arg}z = -\alpha\]

Visualise the 4 quadrants of an Argand diagram?

What is the argument of $3 + 4i$, in terms of $\tan$?

\[\tan^{-1}\left(\frac{4}{3}\right)\]

What quadrant does $3 + 4i$ lie in?

The first quadrant.

What is the argument of $-3 + 4i$, in terms of $\tan$?

\[\pi - \tan^{-1}\left(\frac{4}{3}\right)\]

What quadrant does $3 - 4i$ lie in?

The second quadrant.

What is the argument of $-3 - 4i$, in terms of $\tan$?

\[-(\pi - \tan^{-1}\left(\frac{4}{3}\right))\]

What quadrant does $-3 - 4i$ lie in?

The third quadrant.

What is the argument of $3 - 4i$, in terms of $\tan$?

\[-\tan^{-1}\left(\frac{4}{3}\right)\]

What quadrant does $3 - 4i$ lie in?

The fourth quadrant.

What quadrant does $12 + 5i$ lie in?

The first quadrant.

What quadrant does $-3 + 6i$ lie in?

The second quadrant.

What quadrant does $-8 -7i$ lie in?

The third quadrant.

What quadrant does $2 - 2i$ lie in?

The third quadrant.

For $a + bi$, why shouldn’t you put the signs of $a$ and $b$ in $\tan\left(\frac{b}{a}\right)$?

Because you’re calculating the angle from a triangle, the lengths of the sides can’t be negative.

If $z = a + bi$, how could you write $a$ in terms of $r$ and $\theta$?

\[a = r\cos\theta\]

If $z = a + bi$, how could you write $b$ in terms of $r$ and $\theta$?

\[b = r\sin\theta\]

The rule that $a = r\cos\theta$ and $b = r\sin\theta$ is similar to what in Physics?

\[F_x = F\cos\theta\] \[F_y = F\sin\theta\]

What do you get if you substitute $a = r\cos\theta$ and $b = r\sin\theta$ into $a + bi$?

\[z = r\cos\theta + ri\sin\theta\] \[z = r(\cos\theta + i\sin\theta)\]

What is the $\sin$ and $\cos$ form of $z$?

\[z = r(\cos\theta + i\sin\theta)\]

What is $r\cos\theta$?

\[a\]

What is $r\sin\theta$?

\[b\]

How can you rewrite $ \vert z _ 1 z _ 2 \vert $?

\[|z_1||z_2|\]

How can you rewrite $\text{arg}(z _ 1 z _ 2)$?

\[\text{arg}(z_1) + \text{arg}(z_2)\]

How can you rewrite $z _ 1 z _ 2$ in polar form?

\[r_1 r_2 ( \cos(\theta_1 + \theta_2) + i\sin(\theta_1 + \theta_2))\]

How can you rewrite $ \vert \frac{z _ 1}{z _ 2} \vert $?

\[\frac{|z_1|}{|z_2|}\]

How can you rewrite $\text{arg}(\frac{z _ 1}{z _ 2})$?

\[\text{arg}(z_1) - \text{arg}(z_2)\]

How can you rewrite $\frac{z _ 1}{z _ 2}$ in polar form?

\[\frac{r_1}{r_2} ( \cos(\theta_1 - \theta_2) + i\sin(\theta_1 - \theta_2))\]

How can you rewrite $4(\cos(90^{\circ}) - i\sin(90^{\circ}))$?

\[4(\cos(-90^{\circ}) + i\sin(-90^{\circ}))\]

Why is $4(\cos(90^{\circ}) - i\sin(90^{\circ}))$ not valid polar form?

Because there is a minus in front of the $\sin$.

How can you rewrite $(\cos(\theta) - i\sin(\theta))$?

\[(\cos(-\theta^{\circ}) + i\sin(-\theta^{\circ}))\]

Fixing $(\cos(\theta) - i\sin(\theta))$ relies on what property of $\sin$?

\[\sin(\theta) = -\sin(-\theta)\]

Why is $\frac{16}{3} \pi$ not a valid argument in polar form?

Because it’s not in the range $-pi < \theta \le \pi$.

How could you fix something like $\frac{16}{3} \pi$?

Keep on subtracting $2\pi$ until it’s in the range $-pi < \theta \le \pi$.

Related posts