Further Maths - Polar Coordinates
Flashcards
What is the $y = x$ equivalent for polar coordinates?
What is $x$ in terms of $r$ and $\theta$ for polar coordinates?
What is $y$ in terms of $r$ and $\theta$ for polar coordinates?
What is $r$ in terms of $x$ and $y$ for polar coordinates?
What is $\theta$ in terms of $x$ and $y$?
2021-11-15
$r = a\cos n\theta$
#####
\[r = a\cos\theta\]What does this polar graph look like??
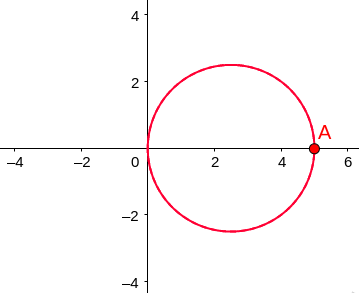
#####
\[r = a\cos\theta\]How would you describe IN WORDS what this look like?? A circle along the $x$-axis starting at the origin and ending after a diameter $a$ long.
\[r = a\cos\theta\]
What does this polar graph look like?

#####
\[r = a\cos2\theta\]What does this polar graph look like??
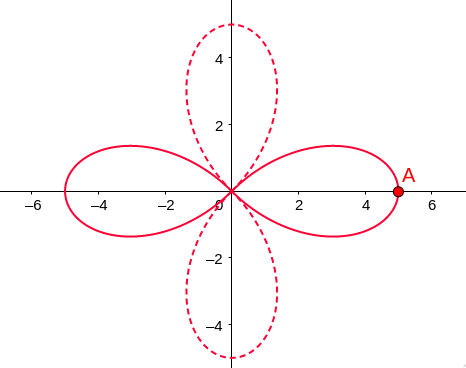
\[r = a\cos\theta\]
How would you describe IN WORDS what this look like?
A circle along the $x$-axis starting at the origin and ending after a diameter $a$ long.
#####
\[r = a\cos3\theta\]What does this polar graph look like??
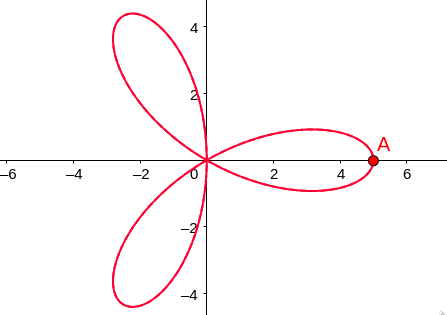
 What is the general polar equation for curves that look like this?
What is the general polar equation for curves that look like this?
 What is the general polar equation for curves that look like this?
What is the general polar equation for curves that look like this?#####
\[r = a\cos4\theta\]What does this polar graph look like??
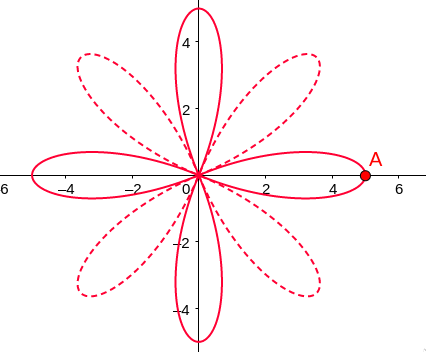
\[r = a\cos2\theta\]
What does this polar graph look like?

#####
\[r = a\cos5\theta\]What does this polar graph look like??
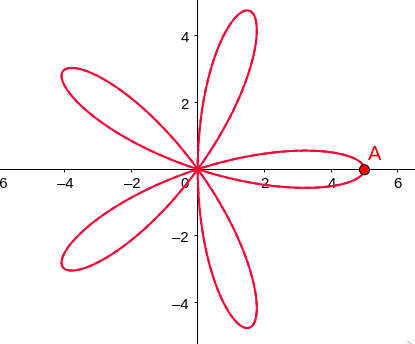
 What is the general polar equation for curves that look like this?
What is the general polar equation for curves that look like this?
 What is the general polar equation for curves that look like this?
What is the general polar equation for curves that look like this?$r = a\sin n\theta$
#####
\[r = a\sin\theta\]What does this polar graph look like??
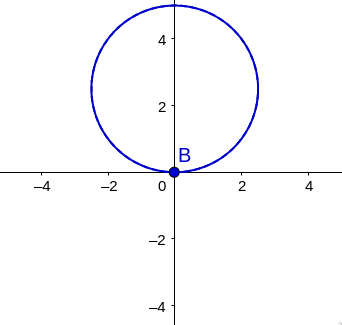
#####
\[r = a\sin\theta\]How would you describe IN WORDS what this look like?? A circle along the $y$-axis starting at the origin and ending after a diameter $a$ long.
\[r = a\cos3\theta\]
What does this polar graph look like?

#####
\[r = a\sin2\theta\]What does this polar graph look like??
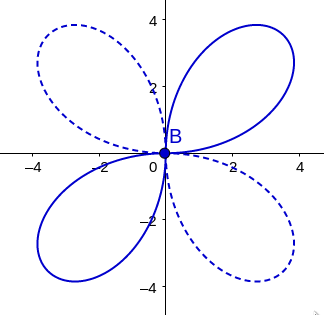
 What is the general polar equation for curves that look like this?
What is the general polar equation for curves that look like this?
 What is the general polar equation for curves that look like this?
What is the general polar equation for curves that look like this?#####
\[r = a\sin3\theta\]What does this polar graph look like??
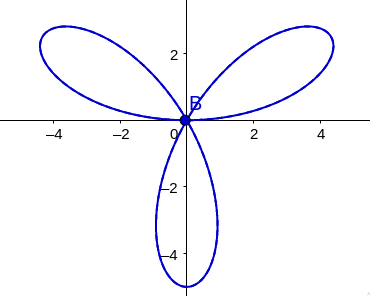
\[r = a\cos4\theta\]
What does this polar graph look like?

#####
\[r = a\sin4\theta\]What does this polar graph look like??
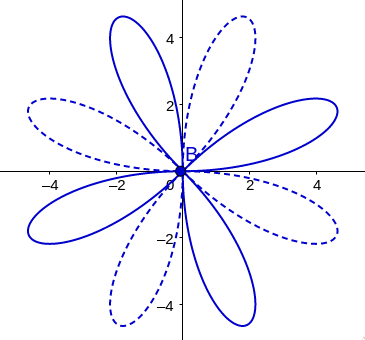
 What is the general polar equation for curves that look like this?
What is the general polar equation for curves that look like this?
 What is the general polar equation for curves that look like this?
What is the general polar equation for curves that look like this?#####
\[r = a\sin5\theta\]What does this polar graph look like??
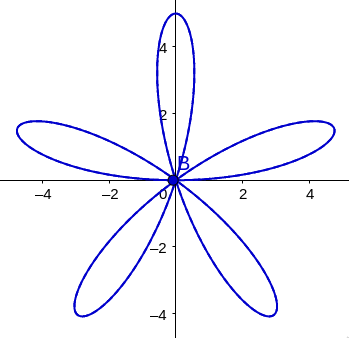
\[r = a\cos5\theta\]
What does this polar graph look like?

 What is the general polar equation for curves that look like this?
What is the general polar equation for curves that look like this?
 What is the general polar equation for curves that look like this?
What is the general polar equation for curves that look like this?\[r = a\sin\theta\]
What does this polar graph look like?

Cardioids
\[r = a\sin\theta\]
How would you describe IN WORDS what this look like?
A circle along the $y$-axis starting at the origin and ending after a diameter $a$ long.
#####
\[r = a + b\cos\theta\]What does this polar graph look like, for $a = \vert b \vert $??
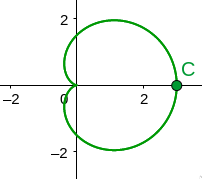
#####
\[r = a + b\cos\theta\]What does this polar graph look like, for $a > \vert b \vert $??
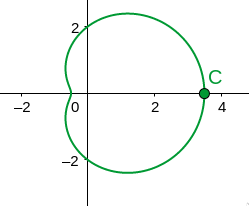
#####
\[r = a + b\sin\theta\]What does this polar graph look like, for $a = \vert b \vert $??
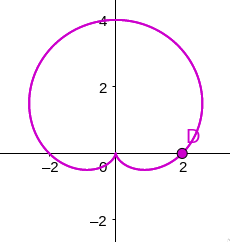
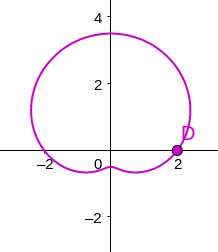
#####
\[r = a + b\sin\theta\]What does this polar graph look like, for $a > \vert b \vert $??
Integration
Given a polar equation
\[r = ...\]what is the formula for the area between angles $\alpha$ and $\beta$??
\[\frac{1}{2} \int^\alpha_\beta r^2 d\theta\]Where does the polar integration formula
\[\frac{1}{2} \int^\alpha _ \beta r^2 d\theta\]come from?? The formula for arc area, $\frac{1}{2}r^2\theta$
 What is the general polar equation for curves that look like this?
What is the general polar equation for curves that look like this?
 What is the general polar equation for curves that look like this?
What is the general polar equation for curves that look like this?2021-11-17
#####
\[x = r\cos\theta\] \[y = r\sin\theta\]Given that $r = \cos\theta$ what is the parametric form of the polar equation with parameter $\theta$??
\[(r\cos^2\theta, r\cos\theta\sin\theta)\]For
\[r = f(\theta)\]what is the formula for $x$??
\[x = f(\theta)\cos\theta\]For
\[r = f(\theta)\]what is the formula for $y$??
\[y = f(\theta)\sin\theta\]If
\[\frac{\text{d}x}{\text{d}\theta} = 0\]what is true about a polar curve for that value of $\theta$?? It is perpendicular to the initial line ($\theta = 0$).
If
\[\frac{\text{d}y}{\text{d}\theta} = 0\]what is true about a polar curve for that value of $\theta$?? It is parallel to the initial line ($\theta = 0$).
\[r = a\sin2\theta\]
What does this polar graph look like?

 What is the general polar equation for curves that look like this?
What is the general polar equation for curves that look like this?
 What is the general polar equation for curves that look like this?
What is the general polar equation for curves that look like this?\[r = a\sin3\theta\]
What does this polar graph look like?
