Thinking, Fast and Slow - Choices
This part of [[Thinking, Fast and Slow, Kahneman]]N is about applying the two-systems model of thought to economics (the study of how people make choices) and challenging the belief that we consistently make rational decisions. Before prospect theory came along, this was the common assumption made my economists.
-
Notes
- Expected Utility Theory
- Prospect Theory
- Mixed Prospects
- Loss Aversion
- (Not) A Contradiction
- Blind Spots of Prospect Theory
- The Endowment Effect
- Bad Events
- Decision Weights
- The Fourfold Pattern
- Rare Events
- Risk Policies
- Keeping Score
- Reversals
- Frames and Reality
- Flashcards
Notes
Expected Utility Theory
The name of this chapter is Bernoulli’s Errors and is about the assumptions that economists used to make. It’s based on a theory of expected utility, a measure of how beneficial a certain outcome would be.
Humans vs Econs
Econs were what Daniel Kahneman called the model that economists had of people at the time. They were rational, selfish and had constant preferences. Think of them like a distorted, sort of alien approximation of humans.
In reality, Humans aren’t rational. They aren’t completely selfish either, and there preferences change from day to day. Human choices are influenced by biases and heuristics and sometimes they don’t make the rational choice.
Simple Models
In decision theory, simple models of bets are often used to approximate more complex everyday decisions. The hope is that these bets share factors which can be applied more generally.
Gambles and bets model the fact that the outcomes of certain choices are rarely certain, every actual significant choice we made comes with some uncertainity.
Students of decision theory hope that the model will be applicable to more interesting everyday problems.
Which do you prefer?
A: Toss a coin. If it comes up heas, you win $100. If it comes up tails, you win nothing.
B: Get $46 for sure.
Rationality and Expected Utility Theory
In most contexts, the rational choice is the one that maximises expected utility. Expected utility theory was not intended as a psychological model, it was designed to build a logic of choice.
Economists adopted it because it describes how decisions should be made, and then extended it to a description of how Econs make choices. This is not correct – humans aren’t always utility maximisers.
Prospect theory is about understanding how actual humans make choices, without assuming anything about their rationality. Prospect theory modifies expected utility theory in order to explain observations about when humans make irrational choices.
Logarithmic Scales and Reference Points
In many psychological phenoma, there is a logarithmic translation between the magnitude of the physical stimulus and the menal “intensity”:
- Raising the energy used to create a sound from $100$ to $1,000$ is the same mental jump from $1,000$ to $10,000$.
- Raising the energy used to make light from $100$ to $1,000$ is the same mental jump from $1,000$ to $10,000$.
Another influence is reference. A reasonably loud noise after total silence is much more jarring than just two reasonably loud noies. Similarly, a bright light in a bright room is percieved much differently from a bright light in a dark room.
Utility as a Logarithmic Function of Wealth
The idea of logarithmic scales has implications for utility, especially those involved with wealth.
- A rich person doesn’t get the same utility from $100$ dollars as a poor person does.
- A gift of $10$ dollars to someone with $100$ dollars is like a gift of $20$ dollars to someone with $200$ dollars.
- We talk about raises as a “30% raise” since the point of reference largely determines the “expected utility” of the raise.
This was Bernoulli’s idea, back in 1738 and it’s where the chapter gets its name. Before this theory, gambles were thought to be determined by the average weighted outcome (think the Law of Total Probability):
The expected value of
80% chance to win $100 and 20% chance to win $10
is $82:
(0.8 x 100) + (0.2 * 10)
Would you prefer this gamble (with expected value 82 dollars) or a sure chance of 80 dollars?
You want the sure chance?? But… you’re not maximising your expected wealth!
Bernoulli’s theory was that the value people see in a gamble is not the weighted average of the possible gain in wealth, but the average weighted utility of the outcomes.
Since the jump from 80 dollars to 82 dollars is marginal in terms of utility, people don’t consider it worth the risk.
| Wealth (Millions) | Utility |
|---|---|
| 1 | 0 |
| 2 | 30 |
| 3 | 48 |
| 4 | 60 |
| 5 | 70 |
| 6 | 78 |
| 7 | 84 |
| 8 | 90 |
| 9 | 96 |
| 10 | 100 |
In this example (roughly $\text{utility} = log _ {10}(\text{wealth})$), the jump from 1 million dollars to 2 million dollars is worth 30 points. Even though the jump from 9 million dollars to 10 million dollars is the same gain in economic value, it’s only worth 4 points.
In fancy economical terms, this is the diminishing marginal value of wealth.
Now consider the bet:
Would you rather have:
* Equal chances to have 1 million or 7 million?
* 4 million with certainty?
If we use the utility rather than economic value, we can compute the value of each bet:
Would you rather have:
* Equal chances to have 1 million or 7 million? (0 + 84)/2 = 42
* 4 million with certainty? 60
And so an individual acting “rationally” would choose the 4 million with certainty option. Economics is finished.
Errors of Bernoulli’s Model
Consider the following situation:
Today, Jack and Jill have a wealth of 5 million.
Yesterday, Jack had 1 million and Jill had 9 million.
Are they equally happy? (Do they have the same utility?)
Bernoulli’s theory would say that since they both have the wealth, they have the utility, and so they should be equally happy. In reality, Jack is likely very happy and Jill is likely very sad.
Instead, their utility is determined by the change in their wealth.
To predict the subjective experience of loudness, it is not enough to know its absolute energy; you also need to know the reference sound to which is automatically compared. You need to know the reference before you can predict the utility of an amount of wealth.
Consider another example:
Anthony's current wealth is 1 million.
Betty's current wealth is 4 million.
They are forced to make a choice:
The gamble: Equal chances to end up owning 1 million or 4 million.
The sure thing: Own 2 million
We might expect the dialog inside their heads to look something like this:
Anthony (current wealth is 1 million):
If I choose the sure thing, my wealth will double with certainity. This is very attractive. Alternatively, I can take a gamble with equal chances to quadruple my wealth or to gain nothing.
Betty (current wealth is 4 million):
If I choose the sure thing, I lose half of my wealth with certainty, which is awful. Alternatively, I can take a gamble with equal chances to lose three-quarters of my wealth or to lose nothing.
Bernoulli’s theory would predict that they would both prefer the sure thing option, since the sure bet by itself has a larger utility than the equal chances.
In reality, Anthony and Betty are going through different decision making processes. They are not thinking in terms of absolute value, but instead of gains and losses.
Since Bernoulli’s theory lacks the idea of a reference point, expected utility theory does not represent the fact that the outcome is good for Anthony and bad for Betty. It can explain Anthony’s risk aversion, but not Betty’s risk-seeking (common behaviour when all options are bad).
This is why a new theory is needed.
Sidenote: Theory-Induced Blindness
The whole idea of prospect theory seems like common sense, of course the reference point should have a bearing on the choices in decisions. The question is, why did it take so long for it be invented?
Firstly, hindsight bias might be at play here. It seems obvious in retrospect, but was probably not so obvious at the time.
Kahneman also presents an idea of theory-induced blindness: once you have accepted a theory and used it as a tool in your thinking, it is very difficult to notice its flaws. If you come across an observation that does not seem to fit the model, you give the theory the benefit of the doubt and assume there must be a perfectly food explanation you are misisng.
Disbelieving is hard work.
Prospect Theory
The solution to all these problems with expected utility theory is prospect theory. Prospect theory is based on three principles:
- Evaluation is relative to a reference point, i.e. it’s based on changes in states of wealth rather than the utility of the states themselves.
- Differences in wealth are diminishing and logarithmic. The subjective difference between 900 dollars and 100 dollars is much smaller than the subjective difference between 100 dollars and 200 dollars.
- Loses loom larger than gains. People are naturally loss adverse – a bet on a sure loss or a chance of a loss is treated different to a bet on a sure gain or a chance of a gain is treated differently.
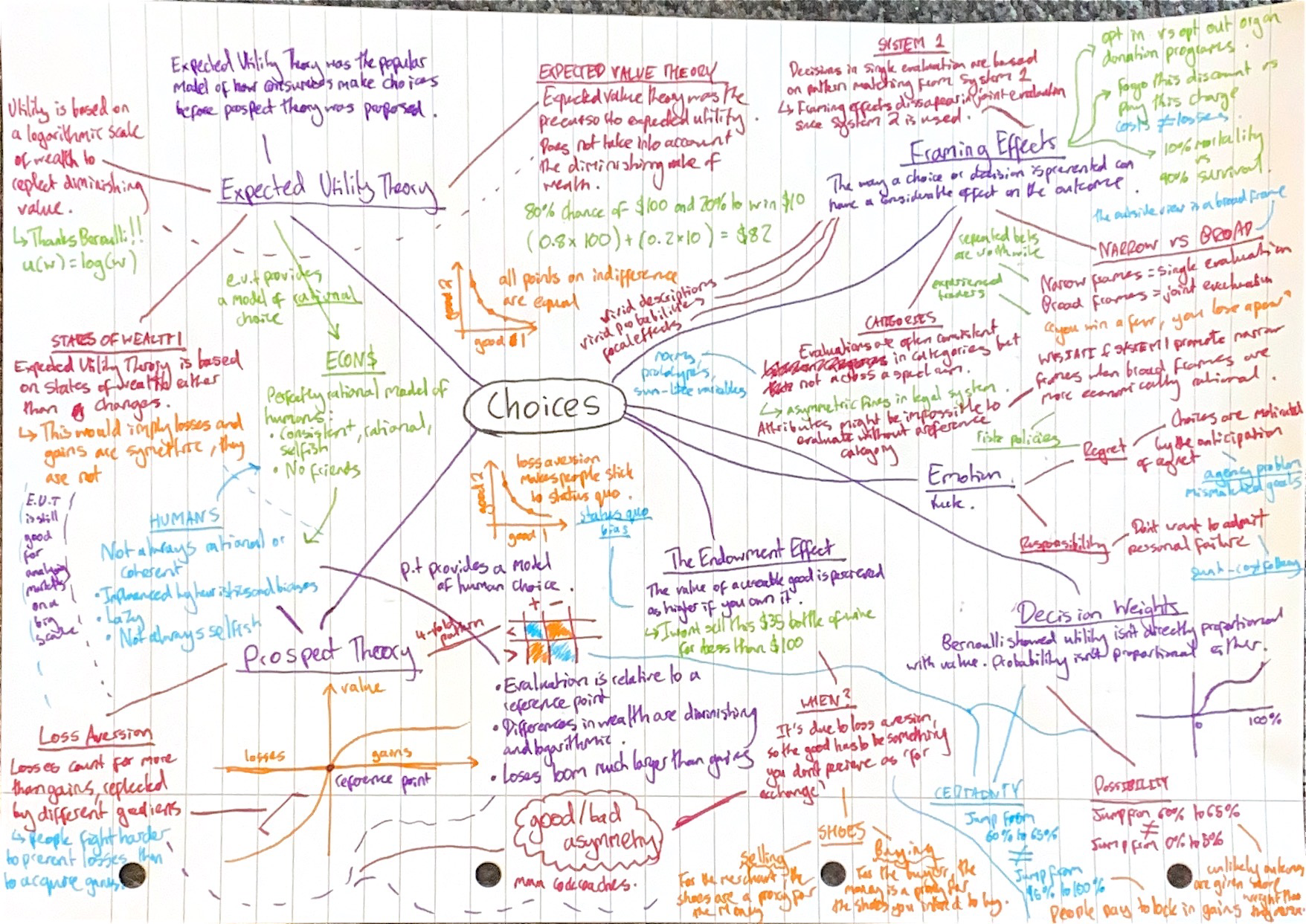
Loses and Gains in Utility Theory
In expected utility theory, the utility of a gain is treated the same as the utility of a loss: as the difference in utility between the two states of wealth:
The utility of gains:
Getting $500 when you have $1,000,000 is the difference between the utility of having $1,000,000 and $1,000,5000, i.e. $500.
...which is equal to...
The utility of losses:
Losing $500 dollars when you have $1,000,000 is the difference between the utility of having $1,000,000 and $999,500, i.e. -$500
(though there would be slight differences in utility since the jump from $999,500 to $1,000,000 isn't the same as the jump from $1,000,000 to $1,000,500 on a logarithmic scale, that's not the point being made here though).
This doesn’t seem right. Consider the following two bets which expected utility theory should treat equally:
Which do you choose?
A. Get $900 for sure
B. 90% chance to get $1,000
Which do you choose?
A. Lose $900 for sure
B. 90% chance to lose $1,000
The subjective value of a 900 dollar gain is more than the 90% chance of 1,000 dollars.
The subjective value of a 900 dollar loss is less than the 90% chance of 1,000 dollar loss.
Another example:
In adition to whatever you own, you have been given $1,000.
You are now asked to choose one of these options:
A. 50% chance to win $1,000
B. Win $500 for sure
In addition to whatever you own, you have been given $2,000.
You are now asked to choose one these options:
A. 50% chance to lose $1,000
B. Lose $500 for sure
Bernoulli’s expected utility theory would imply that these two choices will be answered the same. They are not.
Mixed Prospects
Most bets we have to make in real life try and balance risks and potential gains. For a bank investing in a new business, this is the risk of the business failing or the benefit of the business paying back their loan in full.
There’s two outcomes: victory or defeat.
Loss Aversion
In some examples, we seek risks at the chance for a slightly smaller loss. There are also situations in which we are very loss adverse and heavily avoid risks.
Consider questions like:
What's the smallest gain that I need to balance an equal chance to lose $10?
What's the smallest gain that I need to balance an equal chance to lose $100?
What's the smallest gain that I need to balance an equal chance to lose $1,000?
What's the smallest gain that I need to balance an equal chance to lose $5,000?
You can measure your loss-aversion numerically, as the ratio between the smallest gain required and the loss. This has been estimated to be around $1.5$ to $2.5$ for most people, though it increases as the stakes rise.
For some bets, it is infinite – there is no gain you would take that would balance out a loss, such as the prospect of completely ruining your life.
Traders and those in risky environments are often less loss-adverse.
(Not) A Contradiction
- In mixed gambles, where both a gain and a loss are possible (think investing in a startup for example), loss aversion caues extremely risk-adverse choices.
- In bad choices, where a sure loss is compared ot a larger loss that is merely probable, diminishing sensitivity causes risk seeking.
This contradiction is explained by prospect theory.
- In mixed gambles, the loss looms much larger than the potential gain.
- In bad choices, diminishing sensitivity to loss as it increases causes risk seeking.
Blind Spots of Prospect Theory
Your reference point for the value of a bet might be based on your expectations:
10% chance to win $12 and 90% chance to win nothing.
90% chance to win $1 million and 10% chance to in nothing.
In both situations, the value of “winning nothing” is $0$. However, you might psychologically see the 10% chance to win nothing in the second example as a loss since your expectations are high, which will in turn make you more risk-adverse than in the first example.
Prospect theory cannot deal with the expectation of dissapointment being a factor in the choice you make.
Furthermore, prospect theory assumes all events to be independent, so guilt and regret from previous decisions cannot play a role.
The Endowment Effect
The Endowment Effect is the observation that individuals value an object they own more than the same object when they don’t own it.
Indifference Curves and Prospect Theory
Indifference Curves in Classical Economics
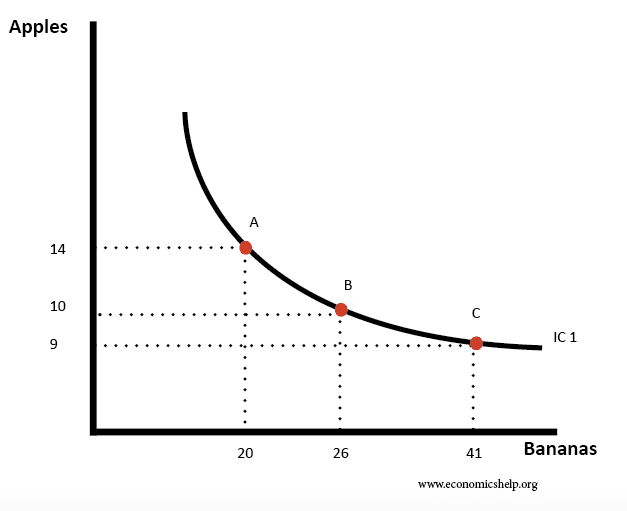
An indifference curve connects the combination of two goods that are equally desirable, i.e. they have the same utility. In the above example, it shows that an individual would be willing to trade 20 bananas for 14 apples.
It is convex because of diminishing marginal utility – when you have a certain amount of bananas, you have all you need. Extra bananas give very little utility, so you would give up a lot of bananas to get something else.
If it was a straight line, the trade between different apples and bananas would be constant since you would be willing to exchange the goods whenever.
All locations on the curve are equally attractive, which is why they are called indifference curves.
Indifference Curves in Behavioural Economics
Now consider the following:
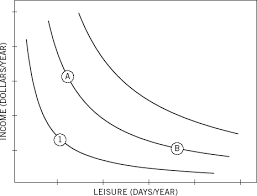
This shows the relationship between the amount of leisure days that an individual has. If a someone has a large income, they will be happy with few leisure days, and if they have lots of leisure days, they will be happy with a smaller income (in fact, they will be equally happy since both points have the same utility).
Again, diminishing marginal utility is demonstrated: the more leisure you have, the less you care about getting an additional day of it.
Classical economics misses a key piece of the puzzle though: it fails to show a reference point. Indifference curves like this one imply that the utility you get from a certain combination is determined soley by the current situation with no regard for the past.
This is much the same way in which it’s wrong to assume bets are based soley on states of wealth, rather than the change experienced when moving from one state to another.
In this classical picture, someone would need little incentive to move from one point on the indifference curve to another which clearly isn’t a reflection of reality. Since losses loom over potential gains, the idea of “losing” your position on the curve would hurt more than the small incentive to move to a new spot.
An Example of How This Applies
Consider two people, Alice and Bob who are “hedonic twins” (they have exactly the same tates, maybe their utility function is the same?) who also have the same starting job.
An offer is placed on the table: one of you can have a salary raise of 10,000 dollars, and another can get 12 extra days of paid vacation a year. Assuming both these combinations are on the indifference curve, Alice and Bob shouldn’t care who gets what.
Assume that they flip a coin, Alice ends up with the 10,000 dollar raise and Bob ends up with the 12 extra days of paid vacation.
In classical economics, they would need very little incentive to swap since both points have the same utility.
In behavioural economics and prospect theory, they would need a lot of incentive to swap. The reasoning goes like this:
- Alice is pleased with the extra 10,000 dollars a year she now makes and doesn’t want to give it up. She would lose 10,000 dollars, in exchange for 12 rest days.
- Bob is pleased with the extra 12 rest days a year and doesn’t want to give them up. He would lose his rest days, in exchange for 10,000 dollars a year.
If losses and gains were symetric, the classical interpretation would be correct. Since losses loom over gains, the loss of their recent reward for outweighs the gain they would get and therefore they stay fixed at one point.
This is manifested in what is called the status quo bias – a preference for the current state of affairs.
The Endowment Effect
As stated at the beginning, the endowment effect is where the value of a good is percieved as higher if you own it. This is because of loss aversion: people feel losses more than they feel gains, and so they price goods higher to make up for it.
Not every good is influenced by the Endowment Effect however, only those that are asymetrically affected by loss aversion.
A shoe merchant doesn’t price shoes higher because he owns them, they are merely a proxy for the money they are hoping to collect from a customer. Likewise, you don’t feel a loss when you pay for the shoes since the money for you is just a proxy for the shoes you intended to buy.
Lots of goods influenced by the Endowment Effect are held “for use” rather than “for exchange”. When you give up a good that is for use, you give away the opportunity to get some utility out of it. There is less of a loss in utility when you gave up something that is for exchange.
The Endowment Effect Examples
Wine Professor
A professor who bought wine at 35 dollars a bottle wasn’t willing to give it up for any price below 100 dollars. This seems wrong, wouldn’t any price between 35 and 100 dollars give some amount of utility?
Traditional expected utility theory implies that the utility comes from the state of having the bottle. Prospect theory suggests that that the willingness to buy or sell the bottle depends on the reference point: the pain of giving up the bottle of the pleasure of getting the bottle.
Music Tickets
People who hold 300 dollar tickets to a sold out musical artist aren’t willing to sell their tickets online for prices up to 3,000 dollars. Again, they can make a huge profit here, why do they not?
Baseball Cards
Inexperienced sellers put higher prices on certain baseball cards at a convention that they owned, rather than experienced ones. This is because they percieved their loss as worse than their gain, whereas more experienced sellers didn’t feel this way.
Questionaires
A set of students were asked to fill out a questionaire for which they would get a reward that was on display the whole time. At the end when they recieved the reward, they were offered the choice to choose an alternate gift. Only 10% changed their minds.
This did not work when the choice was made clear before they actually acquired the reward, they chose the two at roughly the same rate.
Housing Markets
An owner who paid a high price for a house will price it higher than others in a downturn. This means that they spend longer waiting for a buyer and eventually recieve more money.
Poverty
Poverty can be an example of the endowment effect. Poor people live below their reference point and so small gains can still feel like losses, so larger gains feel like reduced losses.
Money that is spent on one good is the loss of another good that could have been purchased instead. For the poor, costs are losses.
Thinking Like a Trader
No endowment effect is expected when owners view their goods as carriers of value for future exchanges, a widespread attitude in routine commerce and in finacial markets.
Traders ask the question:
How much do I want to have that mug, compared with other things I could have instead?
Whereas owners who view their goods ask the different question:
How much do I want to give up my mug?
Bad Events
This chapter elaborates on risk and loss aversion, and gives some wider-reaching examples of the asymetry between good and bad events.
Risk Aversion and System 1
Experiments have shown that we find it much easier to recognise negative and threatening things than we are positive and pleasurable things. This has a reasonable evolutionary backstory: shaving even a few hundredths of a second off the time to recognise a predator increases the odds of living long enough to reproduce.
In the two-systems model of thinking, you could say that risk aversion and perception is more strongly linked into System 1. This also explains why “symbolic threats” also get the brains attention.
It’s easier to recognise bad words like “war” and “crime” than happy words because the associative activation of memory will be similar for words and for real threats since they cover the same concept.
Negative Trumps Positive
A cockroach will completely wreck the appeal of a bowl of cherries, but a cherry will do nothing at all for a bowl of cockroaches.
- Bad emotions have more impact than good emotions
- Bad parents have more impact than good parents
- Bad feedback has more impact than good feedback (or does it? regression to the mean?)
Another example is marriage. An expert on maritial relations says that you need 5 times as many positive interactions than negative ones in order to have a healthy marriage.
Another clear example of negative trumping positive is friendships. It can take years to build up a healthy friendship, but a single bad event can tear it all down.
Positive and Negative are Relative
Much like how prospect theory argues that you need to consider changes rather than states, it doesn’t make a lot of sense to view things as objectively positive and negative.
An example given in the book is to imagine you are out in the country on a cold night, inadequately dressed for torrential rain and your clothes are soaked. A stinging cold winds completes your misery.
As you wonder around, you find a rock that offers a bit of shelter from he elements. A rock isn’t normally a positive thing, but in this context it most definitely is. You love rocks. Rocks are the best.
After a while, the rock will become the reference point and you will long for better shelter, much in the same way that happiness is a moving goalpost.
Most of the time, the reference point is just the status quo.
Loss Aversion in Achieving Goals
Mostly, people are more motivated by the threat of failure than the desire to exceed goals.
Loss aversion represents the asymmetry between losses and gains. Exceeding a reference point is a gain, and ending up below it is a loss. In terms of goals, the gain is exceeding the goal and the loss is not achieving it.
Therefore, the aversion to the failure of not reaching the goal is much stronger than the desire to exceed it.
Taxi Cabs
New York cab drivers have a daily target of earnings. Loss aversion means they want to hit their daily target, not exceed it.
On rainy days, more people get taxis. This means that they can earn a lot more money. On sunny days, less people get taxis and cab drivers often end up just having to drive around to find customers.
Classical economic logic would suggest that cab drivers should make the majority of their money on rainy days and take leisure days when it is sunny. What actually happens is that once they have hit their daily target on any day, they will stop, which means they spend more time driving around on mild days.
This is loss aversion; they don’t want to feel the twinge of guilt for not achieving their day-to-day goals.
Golf
Professional golfers putt more accurately for a par than for a birdie. A par is the reference point, the measure of good. A birdie is one below the par.
Golfers try harder when going for par since failure would mean they were above par, which is a loss. Getting a birdie on the other hand is a gain, which does not count for as much.
Defending the Status Quo
In most cases, the reference point is the status quo. Loss aversion is a powerful conservative force that favors minimal changes, both for individuals and for companies.
Negotiations
In a lot of negotiations, two parties are trying to change the status quo. This could be in international discussions of trade or arms limitations.
One reason they are difficult is because the gain on one side of an agreement is almost always at a detriment to the other. Concessions one side makes are their painful losses, but only mild gains for the other side. This makes it hard to reach agreements.
This can be exploited. Negociators often pretend intense attachment to some good but actually just view the good as a bargaining chip to ultimately give away. Since the other side see the pain that this causes, they are more likely to reciprocate with something equally as painful.
Politics
People fight harder to avoid losses than people fight to earn gains. Reforming taxes might be beneficial for the large majority, but those negatively affected by it will fight tooth and nail to keep it in place.
This is also an explanation for a vocal minority.
Loss Aversion and the Perception of Fairness
Consider the following:
A small photocopying show has one employee who has worked there for six months and earns $9 per hour. Business continues to be satisfactor, but a factory in the area has closed and unemployment has increased. Other small shops have now hired reliable workers at $7 an hour to perform jobs similar to the those done by the photocopying show employee. THe owner of the shop reduces the employee's wage to $7.
Is this:
Completely Fair
Acceptable
Unfair
Very Unfair
Most people would say Unfair/Very Unfair.
Now consider:
The current employee leaves, and the owner decides to pay a replacement $7 an hour.
Is this:
Completely Fair
Acceptable
Unfair
Very Unfair
Most people said this action was Acceptable. The difference is the reference point and the natural aversion to loss. Although both employees would get the same economic value, judgements are made in the first one relative to the reference point.
Now consider if a company becomes more profitable. There is no consensus of obligation for the company to raise the employee’s wages. If losses and gains were symmetric, then there would be the same reaction for a firm decreasing wages and not increasing them.
Decision Weights
This section is actually part of the “The Fourfold Pattern” chapter, but I’ve split it into two.
This section outlines the difference between the weight given to certain options in a decision and their objective probabilities.
Any complex decision about anything involves assigning different weights to the different characteristics. In the decision to buy a car, this might reflect the gas mileage or the amount of previous owners or the decision to take a certain subject might have something to do with the expected amount you’ll learn and the fact that your friends will be there.
Some characteristics are given more weight than others. A very sociable person might consider their friends more or a car fanatic might consider the appearance of a car more.
In the simplified model of bets, the probabilities of different outcomes are a factor that goes into the weight of choosing different outcomes, though they are not equal. The improvement from a 0% to 5% chance to win 1,000,000 dollars is much more than the improvement to 5% to 10%.
Expected Value
Before Bernoulli, gambles were assessed on their expected value. The expected value of a gamble is the average of its outcomes, each weighted by its probability.
Bernoulli retained the method of using the expected value as assesment, but considered the logarithmic nature of our psychological evaluation, the reason for effects like the diminishing marginal value of wealth.
Possibility Effect and Certainty Effect
Benoulli considered the fact that the value is not even. However, he failed to recognise the unevenness of probability.
In the four following examples, the chances of winning 1,000,000 dollars improve by 5%. Does it feel the same?
- From 0% to 5%
- From 5% to 10%
- From 60% to 65%
- From 95% to 100%
The effect of 0% to 5% and 95% to 100% probably felt a lot different from the 5% to 10% and 60% to 65%.
This makes sense: 0% to 5% creates the possibility of a new outcome that didn’t exist before, and 95% to 100% “locked in” the outcome, creating a sense of certainty.
The possibility effect is where highly unlikely outcomes are weighed more than they deserve.
The certainity effect is where outcomes that are almost certain are given less weight than their probability justifies.
They are opposites, at each end of the spectrum. In prospect theory, decision weights are not identical to probabilities.
Probability vs Decision Weight
|Probability (%)|0|1|2|5|10|20|50|80|90|95|98|99|100| |Decision weight|0|5.5|8.1|13.2|18.6|26.1|42.1|60.1|71.2|79.3|87.1|91.2|100|
There’s a clear asymmetry here. Around the middle, the decision weight is approximately equal to the probability. Around the extremetities, this is not the case.
The jump from 99% to 100% is worth 8.8 instead of the jump from 98% to 99% which is only worth 4.1 points. Likewise, the jump from 0 to 1 is worth 5.5 points, whereas the jump from 1 to 2 is worth 2.5 points.
The certainty and possibility effects lie at the extremeties.
Very High and Low Probabilties
Very high probabilities (>99%) and very low probabilities (<1%) are another special case. In most cases, when outcomes seem almost certain (like 99.9999%) we don’t worry too much, the certainty effect is diminished. When outcomes are almost impossible (like 0.0001%), we also ignore them.
This muddles our ability to compare high and large percentages, peiople are almost completely insensitive to risk among small probabilities. A cancer risk of 0.001% is not easily distinguished from a risk of 0.00001%, though the former translates to 3,0000 caners rather than just 30.
Possibility and Certainty Effect Examples
Structured Settlement Purchasing Companies
Imagine you inherit 1,000,000 dollars and your greedy stepsister has contested it in court. You have a strong case, and there is a 95% chance you will get away with all the money.
A structured settlement purchasing company offers to “buy your case” for 910,000 dollars outright. Would you take the offer?
910,000 dollars is less than the expected value of the outcome by 40,000 dollars ($95\% \times 1,000,000$. You feel the certainty effect since you’re more likely to not worry about the small chance of loss – the probability has disproportionaly skewed your perception of the outcome.
Surgery
Notice how the idea of the 5% chance of an amputation during surgery for a loved one feels a lot different to the 10% chance of an amputation during a surgery. The small chance weighs heavily on your mind.
Allais’s Paradox
Allais’s Paradox was an experiment that demonstrated the classical expected utility theory did not describe must people accurately.
In the two following scenarios, which would you choose?
A. 61% chance to win $520,000 or 63% chance to win $500,000
B. 98% chance to win $520,000 or 100% chance to win $500,000
In the first, you’re more likely to pick the 61% chance. In the second, you’re more likely to pick the 100% chance.
This is impossible for a perfectly rational agent. If you compare the two scenarios, the second is just a more favourable version of the first. Why then in the first example are you more likely to sacrifice a 2% chance than in the second example?
Because of the certainty effect. The 2% difference between 61% and 63% is tiny compared to the 98% chance and the 100% chance.
Bug Spray
Suppose that you currently use an insect spray that costs you $10 per bottle and it results in 15 inhalation poisonings and 15 child poisonings for every 10,000 bottles of insect spray that are used.
You learn of a more expensive insecticide that reduces each of the risks to 5 for every 10,000 bottles. How much would you be willing to pay for it?
Because of the certainty effect, people are willing to pay much more for the bottle that reduces risk.
The Fourfold Pattern
The Fourfold Pattern nicely demonstrates the strength of prospect theory over classical expected utility theory.
- High probability of gains: Risk averse
- High probability of losses: Risk seeking
- Low probability of gains: Risk seeking
- Low probability of losses: Risk averse
High Proability of Gains, Risk Averse
95% chance to win $10,000
OR
100% chance to win $9,000
People are likely to take the 100% chance of a lower gain.
People are risk averse here because they fear dissapointement and are likely to accept less than the expected value of a gamble to lock in a large gain. This is what Bernoulli explained with the diminishing value of wealth.
High Probability of Losses, Risk Seeking
95% chance to lose $10,000
OR
100% chance to lose $9,000
People are likely to take the 95% chance of a higher loss.
People who face very bad options take desperate gambles, accepting a high probability of making things worse in exchange for a small hope of avoiding a large loss.
Low Probability of Gains, Risk Seeking
5% chance to win $10,000
People are likely to percieve the value of the bet as higher than it actually is, due to the possibility effect.
This is why lotteries are popular: you can’t win if you don’t play, but the chances of winning are so small.
Low Probability of Losses, Risk Averse
5% chance to lose $10,000
People are willing to pay more money than the expected loss of the bet because of the possibility effect. This is why insurance is bought.
The Fourfold Pattern and the Law
In a case where the plantiff has a strong case with 95% chance of being ruled in their favour, they are sitting in the “High Probability of Gains” section. This explains why they are willing to settle for less than the expected value.
In the same case, the defendant has a 95% chance of losses, so they’re in the “High Probability of Losses”. They are more likely to fight to not settle so they don’t have to pay anything since there is still a sliver of chance.
In frivolous cases, where the plantiff has a weak case with a 5% chance of being rules in their favour, they are sitting in the “Low Probability of Gains” section. The possibility effect makes them fight harder for their claim.
In the same case for the defendant, they have a 5% chace of loss and so are sitting in the “Low Probability of Losses” section. They are more likely to settle for a moderate amount due to the certainty effect.
Rare Events
This chapter is about our perception of rare events. Sometimes we overestimate the chances of something (and therefore percieve the expected value to be higher) and sometimes we underestimate the chances of something.
In summary, events will be overestimated if they attract attention. This can come from things like:
- Obsessive concerns (terrorism)
- Vivid images
- Concrete representations
- Explicit reminders
Associative Activation and System 1
One reason for for overestimation is that there is a strong availability bias. Judgements of the probability of events is affected by the cognitive ease and fluency for which examples came to mind. This can be made worse by things such as availability cascades, which over-emphasise the probability of small events.
Vivid Descriptions
Because associaitve activation leads to overestimating, a vivid description of something is more likely to be rated as more likely as it has a more impactful associative response. This is part of the reason terrorism works so effectively; despite small probabilities of being affected, the threat of bombs is very vivid.
Vivid Probabilities
The way probabilities are described can also have a profound effect on the percieved likihood of events. Consider the difference between these two:
Attorney: "There is 1 false match for every 1,000 DNA tests."
Prosecutor: "DNA tests are 99.9% effective."
The first evokes the image of a man wrongfly put in prison after a DNA test failure, the second fills the heads of the jury with decimal points and makes it seem less likely.
Also consider:
Patients similar to Mr. Jones have a 10% chance of commiting an act of violence against others 6 months after discharge.
Of every 100 patients similar to Mr. Jones, 10 commit an act of violence against another person within 6 months of discharge.
The more vivid description produces a higher weight
Focal Effects
Another reason for overestimation is focal effects, where focusing on a certain example makes it feel like it is more likely. In an experiment where individuals were asked to rate the likelihood certain individual basketball teams would win, the combined probability at the end was 240%. By considering them one at a time instead of all at once, there was a focal effect that changed their decision.
This could also be explained in the context of associative activation: the idea of a specific thing has a strong associative response and therefore a larger availability, whereas the vague notion of “the others” doesn’t and so isn’t accounted for as much.
Underestimating
- Not enough people take action against climate change since there’s no vivid example of it (but people are more scared of Californian earthquakes since they’ve lived through one).
- Not enough was done before the 2008 financial crisis in preperation since no one had experienced one, there was no memory or description to go off of.
Risk Policies
A risk policy is a broad frame that routinely applies whenever a relevant problem arises. Risk policies ensure positive consistency across different decisions where we are naturally inclined to make the wrong ones.
Broad vs Narrow Framing
Consider the following pair of decisions, reading both of them first before making your choice:
Decision 1: Choose between
A. Sure gain of $240
B. 25% chance to gain $1,000 and 75% chance to gain nothing.
Decision 2: Choose between
C. Sure loss of $750
D. 75% chance to lose $1,000 and 25% chance to lose nothing.
What two decisions do you make? Most people go for A and D, being risk-averse on the first and risk-seeking on the second. Now consider this:
Choose between:
AD. 25% chance to win $240 and 75% chance to lose $760
BC. 25% chance to win $250 and 75% chance to lose $750
BC is clearly the best option here – the chances are equal to the first option, but you still end up with a higher expected value overall. But these two examples are actually the same:
-
Afollowed byDin the first example is 240 dollars for definite, with a 75% chance to lose 1,000 dollars. That means that 25% of the time you just get 240 dollars but 75% of the time you lose 1,000 as well, which would mean in total you’d get 760 dollars (1,000 - 240). -
Bfollowed byCin the first example is a loss of 750 dollars for definite. 25% of the time, you’ll earn 1,000 dollars though which will mean you will have 250 dollars overall.
The rational choice to make is BC. Looking at each seperate problem seperately was worse than looking at the overall combination. This shows how inconsistent humans are with their preferences… it’s the same bet but different choices are made.
This is narrow vs broad framing. In a narrow frame, the overall value was determined by two simple decisions considered seperately. In broad framing, it was considered as a single comprehensive decision.
WYSIATI and a natural aversion to mental effort means that most of the time, humans use a narrow frame when making decisions. We don’t have the inclination or the mental resources to enforce consistency in our preferences. Our preferences aren’t magically consistent or coherent like they are in a rational agent model.
Repeated Bets
Consider another example:
Would you accept a gamble on the toss of a coin in which you could lose $100 or win $200 dollars?
Since we are naturally risk-averse when it comes to high probabilities of losses, we are unlikely to accept that bet.
But would you accept the bet if you got to repeat it 100 times?
After a 100 times, the bet has an expected value of 5,000 dollars, and so anybody would probably take the bet. If you were to use a narrow frame and consider each bet seperately, you’d be seriously missing out on the payout.
The Mantra of Economic Rationality
you win a few, you lose a few
In isolation, bets with a marginal difference between expected losses and gains seem like a terrible idea. Unless you’re deciding what option to take on your last ever bet however, it pays to consider the aggregation of expected value.
- This only works when gambles are independent of each other. Investments in the same industry will all go bad together.
- It only makes sense when the possible loss does not cause you to worry about your total wealth.
- It should not be applied to long shots. (?)
Experienced Traders and Broad Framing
Experienced traders use broad framing to shield themselves from the pain of losses. If they were incredibly risk averse, it’s unlikely an investment would ever come up that was worth the risk by itself.
Over a long period of time, even bets with small gains compared to losses will come out on top.
This is why checking a portfolio every day would be a bad idea. The pain of the frequent small losses exceeds the pleasure of the equally frequent small gains. Furthermore, the typical response to short-term bad news is increased loss aversion, which lowers their opportunities for the future.
You’re also less likely to “churn” your portfolio. Remember in [[Thinking, Fast and Slow - Overconfidence]]N were the more trades that got made were associated with decreased financial performance.
Experienced traders think with broad frames, inexperienced traders think with narrow frames.
Risk Policies
A risk policy is a broad frame that routinely applies whenever a relevant problem arises. Risk policies ensure positive consistency across different decisions where we are naturally inclined to make the wrong ones.
“Never buy extended warranties” is an example. The threat of a device breaking looms heavily, but you save more money overall by not buying extended warranties than you do to fix the occasional broken product.
The Outside View as Broad Framing
The outside view shifts the focus from the specific to the general, a broad frame for thinking about plans.
The outside view is a risk policy that applies to decisions.
Keeping Score
Most people aren’t motivated to earn money for economical value alone. Instead, money is a proxy for points on a scale of self-regard and achievement. We reward and punish ourselves by keeping track of these internal scores.
This disconnect is responsible for biases and fallacies that Econs just don’t have. We refuse to cut losses when doing so would admit failure (sunk cost fallacy), try to avoid regret as much as possible and let our sense of responsibility over our actions dictate our choices.
The ultimate currency that we strive for is emotional. This creates conflicts of interest when an individual has to act as an agent on behalf of an organisation (the agency problem).
- People create mental accounts, like treating investments in different stocks seperately rather than considering the value of the overall portfolio:
- Contributes to the sunk cost fallacy, “closing” a mental account with a negative balance makes you feel regret: stay for too long in poor jobs, stay in a unhappy marriage, spend too long on an unpromising research projkect.
- Responsible for the disposition effect where you sell assets that have increased in value while keeping assets that have dropped in value.
- This is narrow framing – it helps us make decisions that seem like a good idea locally but not a good idea overall.
- When acting on behalf of an organisation, the mental accounts don’t match up with the firm’s overall goal of making the most amount of money. Boards of directors often replace CEOs not because their performance will be better but because they don’t have to care about sunk costs.
- We make decisions based on the expectation of regret:
- Regret is when you feel sad or dissapointed over not taking a different course of action. Sinking feeling that you’ve lost opportunities and made a mistake.
- Regret is triggered by the availability of alternatives to reality, feel more regret over deviation from the normal than staying with the normal and seeing what benefits there were from deviating.
- In general, people have stronger emotional reactions to outcomes that are produced by action rather than the same outcome when it is produced by income.
- Regret is worse when we have responsibility.
- Hindsight bias exercebates the effect since we see ways we could have prevented something.
- Anticipate more regret than we actually feel, part of a “psychological immune system”.
Reversals
Reversals are about inconsistencies that arise from considerations in broad and narrow frames. A rational agent’s choices wouldn’t depend on the context in which the choices are made, which is something that affects humans greatly.
Rationality is served by broader and more comprehensive frames.
Joint vs Single Evaluation
In [[Thinking, Fast and Slow - Heuristics and Biases]]N, we saw that joint and single evaluations can lead to different evaluations. We now understand the concept of a broad and narrow frame which provides additional explanation for this behaviour.
In single evaluation, we are not asked to compare anything and so there is no reference or context in which we can make our considerations. This means that we more heavily rely on the emotional response of System 1 and use intensity matching to make judgements.
In joint evaluation, we need to compare different scenarios and outcomes. Joint evaluation requires a more careful and effortful assessment, which calls for System 2. This means we’re more likely to be consistent.
Consistency in Categories
When we make judgements, we often have an idea of the relevant norm or prototype in which we can compare our choices.
John is 6 years old. He is 5' tall.
Jim is 16. He is 5'1" tall.
Who is taller?
In single evaluation, we asses John’s tallness is comparison to the average height of 6 year olds, and assess Jim’s tallness in comparison to the average height of 16 year olds. Therefore, we might say that John is tall and Jim is short.
However, in joint evaluation, the age is no longer a factor and we can compare the two.
This shows consistency within categories. If Jim was also 6, it would be easy to recognise Jim being taller. Judgements and preference are coherent within categories but potentially incoherent when the objects that are being evaluated belong to different categories.
Inconsistency Across Categories
Dolphins in many breeding locations are threatened by pollution, which is expected to result in a decline of the dolphin population. A special fun supported by private contributions has been set up to provide pollution-free bredding location for dolphins.
Single evaluation: we made an emotional assesment of how “good” dolphins are compared to other animals (the category), and we use intensity matching to assign a dollar value.
Farmworkers, who are exposed to the sun for many hours, have a higher rate of skin cancer than the general population. Frequent medical check-ups can reduce the risk. A fund will be set up to support medical check-ups for threatened groups.
Single evaluation: we make an emotion assesment of how important farmers getting skin cancer is in comparison to other public health issues (the category), and we use intensity matching to assign a dollar value.
In single evaluation, the dolphins get larger donations on average. In joint evaluation, the fact that farmers are human and dolphins are not is recalled and so farmers will get larger donations.
The narrow framing of the single evaluation allowed dolphins to have a higher intensity score, learding to a high rate of contributions by intensity matching.
This is relevant in law too. Juries are shown compensation cases in single evaluation, which means that choices which seem coherent in their categories don’t seem fair in joint evaluation.
Case 1: A child suffered moderate burns when his pajamas caught fire as he was playing with matches. THe firm that produced the pajamas had not made them adequately fire resistant.
Case 2: The unscrupulous dealings of a bank caused another bank a loss of $10 million.
In single evaluation, the compensation for the child is much lower than it is in joint evalation. The ethics of giving huge amounts of money to a bank vs giving small amounts of money to a child is given consideration.
Evaluability Hupothesis
Some attributes can’t be evaluated in single evaluation because numbers are not “evaluable” on their own. In joint evaluation, you can evaluate attributes relative to one another.
Frames and Reality
The way in which a choice is stated can have a considerable effect on the outcome. This should not be true of rational agents – the formulation of a choice shouldn’t make any difference in logical reasoning.
People are sensitive to inconsequential factors that determine their preferences.
Framing Effect Examples
Italy won the 2006 world cup.
Frace lost the 2006 world cup.
“Won” evokes different associative responses to “lost”, although the two statements describe the same situation, System 1 interprets the meaning differently.
Would you accept a gamble that offers a 10% chance to win $95 and a 90% chance to lose $5?
Would you pay $5 to participate in a lottery that offers a 10% chance to win $100 and a 90% chance to win nothing?
“Lose” evokes stronger negative feelings than “pay”, costs aren’t given the same emotion weight as losses.
The one-month survival rate of surgery is 90%.
There is a 10% mortatility rate of surgery in the first month.
First one is optimistic, second one is scary death stuff.
Would you sign this form to opt-in to organ donation?
Would you sign this form to opt-out of organ donation?
Signing a form takes a lot of effort. For the majority, your desire to donate organs isn’t motivated by moral choices but by the willingness to sign a form and a natural aversion to effort.
Would you forgo this discount?
Would you pay this surcharge?
Costs do not equal losses, we don’t consider them equal. This is why Clubcard offers in Tesco aren’t labelled as surcharges to non-clubcard holders.
Frames and System 1
Our decision making is influenced by the associative response of System 1. Since we’re naturally lazy and effort-averse, most of the time we just follow on with the suggestions.
This poses problems when logically equivalent statements evoke different associative responses. This links back to Rare Events, in which the emotional framing of the choice influences the decision.
Economically equivalent does not equal emotionally equivalent.
Empty Intuitions
Our personal feelings on certain issues are based on moral intuitions. Moral intuitions are attached to frames and descriptions rather than reality.
Therefore, it doesn’t seem right to think about framing as an intervention that masks or distors and underlying preference. Without moral intuitions, we might not have any actual preferences. Our preferences are about framed problems, and our moral inutitions are about descriptions, not about substance.
Useful Frames
Intentional reframing can be beneficial. The idea of risk policies is about using a broader frame in order to deliver the most economic benefit.
Another place where frames can be useful is dealing with the sunk-cost fallacy. If you think about sunk-costs in general rather than as specific “mental accounts”, you can make more rational decisions.