Thinking, Fast and Slow - Heuristics and Biases
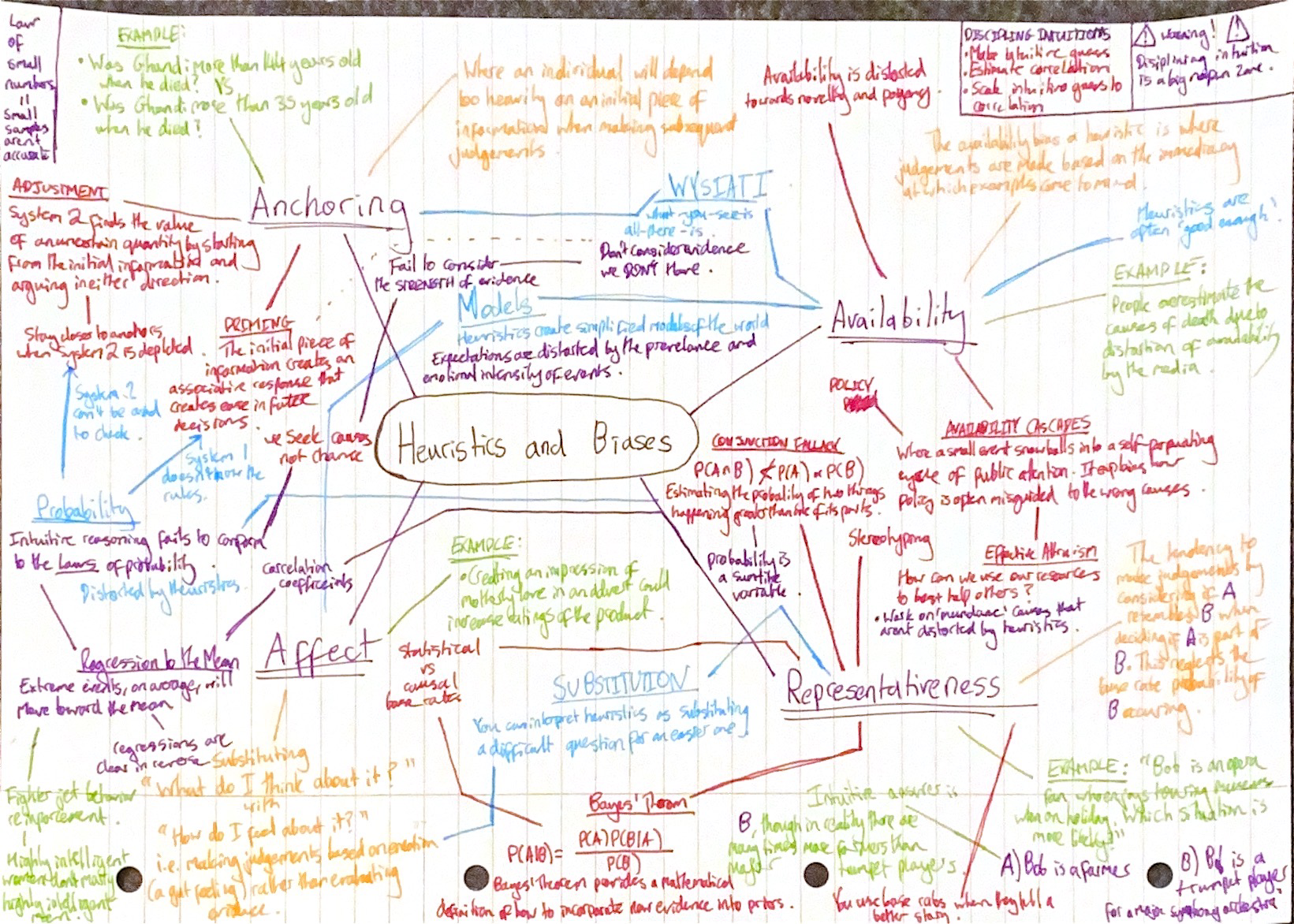
This part of [[Thinking, Fast and Slow, Kahneman]]N details the shortcomings of our own decision making that are a result of the two different forms of thinking. It covers heuristics, roughly a “rule of thumb”, and baises, systematic errors that come from the reliance on heuristics.
The common thread that runs through many of these flaws is that we often fail to consider how limited our evidence is.
- Notes
- Flashcards
Notes
The Law of Small Numbers
The Law of Small Numbers or insensitivity to sample size is a cognitive bias that occurs when people judge the outcomes of a statistic without respect to sample size.
The Law of Large Numbers
The Law of Large Numbers states that as a sample size grows, the mean gets closer to the average of the whole population.
This is commonly used to back up studies: if large samples are more precise than small samples, then a study with a large sample is likely to be correct.
The Law of Small Numbers
The Law of Small Numbers is a joke name for the reverse: small samples are likely to representative.
The problem is that the brain is wired in such a way that makes it easy for us to believe that small samples are accurate when in reality, most surprising results can be explained through chance. In fact, extreme results are more likely with a small sample size: you’re much more likely to get three heads in a row than you are eight heads in a row.
It follows from this:
- Large samples are more precise than small samples.
- Small samples yield extreme results more often than large samples do.
Example: Kidney Cancer
Both of the following statements are true.
The counties of the United States with the lowest incidence of kidney cancer are mostly rural, sparsely populated, and located in traditionally Republican states.
Initially, a few explanations may pass through your head… this is the associative machinery of System 1 giving suggestions to System 2:
- Repulican politics offer better healthcare. (Unlikely)
- Rural and sparsely populated towns are more “at one with nature” and don’t have problems with things like pollution. (More likely)
The counties of the United States with the highest incidence of kidney cancer are mostly rural, sparsely populated, and located in traditionally Repulican states.
If you hadn’t been aware of the conflict, explanations like these might pass through your head:
- Republican politics offer worse healthcare. (Questionably likely)
- Rural areas are affected by more poverty, which could also impact healthcare. (More likely)
This is a result of the Law of Small Numbers. Counties with small populations are much more likely to have extreme variations in the prevelance of kidney cancer.
For example, a city with 10000 people in is more likely to have a sample closer to the actual mean of the whole population opposed to a town with just 20.
It’s an accident of sampling.
Artifacts
An artifact is an observation produced entirely as a result of the of the research method. In the Kidney cancer example, the quirk that the lowest kidney cancer counties have small populations is because the sample size is small. It’s an artifact.
Researchers Choose Bad Sample Sizes
Because of the intuitive overconfidence in our beliefs, researches are likely to choose sample sizes that mean there is a margin of error sometimes of over 50%. There’s a well defined mathematical process for picking a sample size that will minimise this rist, but most overlook it and trust their gut (intuitive statistics from System 1) instead.
It’s always a good idea to treat statistical intuition with proper suspicion and replace our impressions with actual computed, mathematical results.
Stories vs Results
A theme in [[Thinking, Fast and Slow - Two Systems]]N was that we’re more likely to accept things because we can tell a good story or make a good model with them, rather than on the quality of evidence. This is a consequence of a lazy System 2 and a System 1 that is hardwired to find causal connections. Furthermore, System 1 doesn’t even make the uncertainty clear – it just marches on, supressing doubt.
The Law of Small Numbers is not a one-off bias that occurs, it’s a symptom of a more general bias that favours certainty over doubt and the fact that we are prone to exaggerate the consistency and coherence of what we see.
Intuitive Chance
BBBGGG
GGGGGG
BGBBGB
Which is least likely? Many people will say “GGGGGG” when really any sequence is just as random as the others. It’s the same reason that picking identical lottery numbers, such as 1 1 1 1 1 is just as likely as any other combination.
This is because we are pattern seekers in which regularities don’t appear by accident but as the result of “mechanical causality”. We do not expect to see regularity produced by a random process, and if a we seemingly detect a pattern in a random sequence, we no longer think it’s random.
Hot Hand
In basketball, or really any other sport, there’s a notion that sometimes people get a “hot hand” and their ability to play the game increases for a short period of time. Research from data of basketball games and other sports has shown this is false: there’s no reason other than chance.
This explains why it’s difficult to judge people based on their ability without a large sample size. You might think a CEO is good because he handles 3 mergers very well, but this could all be down to chance. You might also think you’re especially good at choosing stocks because you made 2 good trades, when really the [[Efficient Market Hypothesis]]N suggests that you’ll eventually regress to the mean.
Example: Funding for Small Schools
The Gates Foundation gave $$1.7$ billion to a project to fund smaller schools after research that surveyed the effectiveness of different schools. Many top-ranking schools had fewer pupils, and so the intuitive conclusion was that small schools have better teaching facilities.
It’s even easy to come up with a causal mechanism behind the research, something like “less students means that each pupil gets more individual attention”.
This is not true – many of the lowest-ranking schools also had fewer pupils. You could rationalise this like “a larger number of students means that there are more resources available to everyone”. Instead, this was because each small school had a small sample size and so there was more extreme results.
Anchors
Anchoring is where an individual will depend too heavily on an initial piece of information offered when making subsequent judgements during decision making.
Anchoring Examples
Ghandi
- Was Gandhi more than 114 years old when he died?
- Was Gandhi more than 35 years old when he died?
Followed by:
How old was Ghandi when he died?
People asked the first question are more likely to give a higher number.
Redwoods
- Is the height of the tallest redwood more or less than 1,200 feet?
- Is the height of the tallest redwood more or less than 180 feet?
Followed by:
How tall is the tallest redwood?
People sked the first question are more likely to give a higher number.
Germany
- Is the annual mean temperature in Germany higher or lower than 20 degrees Celcius?
- Is the annual mean temperature in Germany higher or lower than 5 degrees Celcius?
Followed by:
What is the annual mean temperature in Germany?
Estate Agents
A study was done that had real estate angents go into a house and assess its worth. They were given access to a pamphlet that contained a listed asking price.
The asking price on the pamphlet was higher in one group than it was the other.
The estate agents had to give a reasoned conclusion about the reasonable buying price.
Even though the asking price on the pamphlet affected their answers considerably, they did not list it as one of the factors that they considered, something obviously not true.
When non-estate agents went through the same task, there was a similar effect but they said that the asking price did affect their judgement.
Donating To Charity
- Would you be willing to pay 5 dollars to save some poor starving children?
- Would you be willing to pay 400 dollars to save some poor starving children?
I’ve noticed this myself. If I see a pay-what-you-want donation, the suggested prices have a large impact on the amount I would consider donating.
Negotiating
Anchoring explains why the initial starting value of an offer has a large impact on the final outcome of the price.
- The starting value of an auction.
- The initial price of a piece of fine art.
- The offer from a seller.
In order to counter anchoring effects from outrageous proposal when negociating, you can:
- Come back with an extravagantly low number to bridge the gap.
- Make it clear to the other side that the offer is off the table.
System 2: Anchoring as Adjustment
One reason for the anchoring effect is the process of adjustment by System 2: to find the value of an uncertain quantity, start from the anchoring number and adjust your estimate by arguing either for an increase or a decrease from the initial number.
This explains why you’re more likely to speed when coming from a motorway to a city, you use the anchor of the initial speed limit and then misappropriately adjust it down.
A consequence of this is that the willingness to exert mental effort will affect the amount you deviate from an anchor. Adjusting an anchor rationally requires mental effort, and so if you’re mentally lazy or have a depleted ego (?) then you are likely to be influenced more by an anchoring effect.
System 1: Anchoring as Priming
Another reason for the anchoring effect is priming of associative memory by System 1. System 1 doesn’t know whether it’s true or not, but there is an associative activation as if it is true.
The automatic activation of certain concepts which change depending on the initial anchor will activate different sets of ideas in memory. This will bias your choices when thinking slowly about it later on since the ideas associated with the anchor will be “closer”.
Anchoring in System 1 and System 2, WYSIATI
Anchoring is therefore a result of a failure of System 1 and a failure of System 2. System 2 works on data that is retrieved from memory but the biasing influence of anchors in System 1 make specific ideas easier to retrieve.
Furthermore, System 2 has no idea this occurs. This goes back to WYSIATI: it’s an automatic operation and you don’t consider the alternate viewpoints. You have no clue that you might be missing information.
So What? + Absurd Anchors
This may seem like a perfectly rational thing to do: of course the initial information should provide a bearing on the overall answer. This is true, but it doesn’t make up for the fact that absurd anchors have an effect on the answer too.
Was Ghandi older than 144 years old when he died?
This has a similar affect to a question where he was said to be 100 years old. What’s more, even completely random numbers will influence a decision. In the book, they rigged a wheel of fortune to give either 10 or 65 and when participants looked at these numbers before answering a percentage question, their answers were biased.
Anchoring Index
Unlike other cognitive biases, anchoring is easy to quanitfy. The anchoring index is the ratio between the difference between two anchors and the difference between the mean of the responses when the anchor was used.
\[\text{anchoring index} = \frac{\text{diff. in responses}}{\text{diff. between anchors}}\]This normally is around $40\%$. $0\%$ would mean there was no difference in affect from an anchor and $100\%$ would mean that people adopted the anchors as the estimate without modifying them.
Availability and Affect Bias
The availability bias or the availability heuristic is a cognitive bias in which decisions are influenced by the immediacy of certain examples instead of the quality or quantity of evidence.
Availabilty Examples
Insurance and Disasters
People are more likely to buy protective insurance after a natural disaster, such as after a Californian earthquake. This is despite the fact that the probability of an earthquake remains constant.
As the memory of the earthquake dies down over time, so do protective measures. This leaves people inadequetly prepared for the next one in an unforgiving cycle.
I’m sure the same will happen with the coronavirus: there will be a time when everyone is still worried about infection from all types of diseases that decreases over time as people forget about it (and what is there to remember too).
Finally, the book also gives the example that people are as cautious about disasters as their worst memory. This means that people only prepare for the case they’ve seen so far, not the worst-case scenario.
(The example given was of pharonic Egypt, where societies tracked the high-water mark of rivers assuming that the floods will not rise higher than the existing high-water mark. This was not always the case).
Causes of Death
People overestimate the likelihood of certain causes of death based in proportion to how easily an example comes to mind, which is heavily skewed by media coverage.
From the book
- Strokes kill almost twice as many people as all accidents combined, but 80% said accidental death was more likely.
- Tornadoes were judged as more frequently killing people than asthma, despite the fact the latter causes 20x more deaths.
- Death by lightning is 52x more frequent than death from botulism, but botulism-related deaths were judged more likely.
- Death by disease is actually 18 times more likely than accidental death, but they were judged as equally likely.
- Death by accidents were judged to be more than 300 times more likely than death by diabetes, the real ratio is 1:4.
Media coverage is biased towards novelty and poignancy – they’re much more likely to report a strange accident where someone ends up dying from a piano being dropped on their head rather than a routine death from diabetes.
The world in our heads is not a precise replica of reality; our expectations about the frequency of events are distored by the prevalence and emotional intensity of the messages to which we are exposed.
The Affect Heuristic
People make judgements and decisions based on their emotions: Do I like it? Do I hate it? How strongly do I feel about it?
This is an example of substituion: “What do I think about it?” becomes “How do I feel about it?”.
When people think something is good, they are able to list more advantages than disadvantages. The opposite is also true, if someone thinks something is bad, then they will think of lots of disadvantages rather than advantages.
This is different from reality where there are numerous tradeoffs between seperate things. A benefit might come at the cost of a disadvantage, but that is rarely reflected in people’s opinions.
In a study where people were asked to list the advantages and disadvantages of something before being given information that gave more benefits or disadvantages, the precense of advantages decreased the amount of risks people saw in a product despite there being no change in evidence.
It’s like saying, “Don’t eat that banana, it’s covered in cynaide!” and then someone else saying “But it is good for you” and you magically forgetting about the fact it’s covered in cyanide because you think positively of the banana. It doesn’t really work like this, but it happens all the time.
Policy and Availability Cascades
A lot of policy and regulation is a reaction to public pressures more than objective and rational analysis. One example is the Love Canal affair in which a small amount of toxic material being released into water by chance caused a huge focus for years on the regulation of toxic waste.
This is a good thing, though the funding could’ve been placed elsewhere and saved many more lives. Instead the policy was fuelled by the public’s adverse, emotional reaction to the story rather than a weighted analysis of the costs.
An availability cascade is the process by which a very small and relatively minor event turn into a public panic and large-scale government action. The Love Canal affair is an example of this.
- A small media story about a risk catches the attention of a segment of the public.
- The public become worried.
- The emotional reaction of the public becomes a story in itself.
- The news reports on this, which generates additional, wider coverage.
- This makes the public more worried.
The loop turns small events into big events.
Effective Altruism?
I may be drawing the wrong connection here, but the availability heurstic and availability cascades are one of the things that I think effective altruism tries best to avoid. By focusing on where money or aid is best placed instead of where it looks like it is, you can potentially do more good.
From the book, the legislation that came about as a result of the Love Canal affair created a 1.6 billion dollar fund, considered a triamph of environmental policy. However, that 1.6 billion dollars could be put to use somewhere else where it would be much more effective.
Small Risks or Big Risks
A recurring theme is that our intuitions are based on the best story or model of the situation that we can imagine, rather than on the quality of facts or evidence. This causes us to overexaggerate small risks.
This, alongside availability cascades, means that small risks get spread around hugely, creating bloated representations of actual issues.
Representativeness Heuristic
That’s a mouthful. The representativeness heuristic is the tendency to make judgements about whether an object or event A belongs to class B by not considering at the degree to which A resembled B.
When we use the representativeness heuristic, we reglect the general probability of B occuring. This is called the base rate.
Representativeness Examples
Bob is an opera fan who enjoys touring art museums when on holiday. Growing up, he enjoyed playing chess with family members and friends. Which situtation is more likely?
- Bob plays trumpet for a major symphony orchestra
- Bob is a farmer
Most people say that the first is more likely, despite the fact that there are many times more farmers than there are Trumpet players in major symphony orchestras.
You judge the probabiblity based on the representativeness – Bob looks like the kind of person who is a trumpet player, based on a stereotype. In reality, the base rate is much higher for farmers.
Substiution
Using representativeness as a shortcut is a clear example of a substitution. Instead of answering the difficult, System 2 type question “What’s the probability that Bob is a trumpet player?”, we ask the question “To what extent does Bob look like a trumpet player?”.
This is a consequence of mental shotgunning: when asked a question about something, we automatically and subconciously compute the similarity, which we end up using to make our judgements.
Good, Some of the Time
Representativeness is a good mental shortcut in most situations. The book gives the following examples:
- People who act friendly are in fact friendly.
- A professional athlete who is very tall and thin is much more likely to play basketball than football.
- People with a PhD are more likely to subscribe to The New York Times than people who ended their education after high school.
- Young men are more likely than elderly women to drive aggressively.
There is some truth to these statements, and so predictions that follow might be accurate.
Base-Rates Aren’t For Cool Kids Only
Everyone uses base-rates when they need to. In the Bob example, if you were just asked to predict the probability that Bob is a farmer instead of a trumpet player in a major symphony orchestra without a description, you would consider the fact that there are a lot more farmers than trumpet players.
But when given the occupational stereotype, most of the time the idea of taking into base rates doesn’t even cross your mind. This is an example of WYSIATI, how can you take into account base rates when you don’t think of them?
Disciplining Intuition
Reject evidence by default, and examine if it is true. Keep your judgements of probability close to the base rate. Make sure your beliefs are constrained by the logic of probability – two independent events occuring is less likely. If something has a 90% chance of occuring, it has a 10% chance of not occuring.
Bayes’ Theorem
Bayes’ Theorem provides the mathematical definition of how you should incorporate new evidence into prior probabilities to form an updated probability estimate.
Conjunction Fallacy
The conjuntcion fallacy occurs when one someone estimates the probability of two things happening (a conjunction of two events) as being more probable than at least one of its component probabilities. You could think of it like assuming specific conditions are more probable than general ones.
Conjunction Fallacy Examples
Linda
Linda is thirty -one years old, single, outspoken and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in antinuclear demonstrations.
Which is the most likely:
- Linda is a teacher in an elementary school.
- Lnda works in a bookstrore and takes yoga classes.
- Linda is active in the feminist movement.
- Linda is a psychiatric social worker.
- Linda is a member of the League of Women Voters.
- Linda is a bank teller.
- Linda is an insurance salesperson.
- Linda is a bank teller and is active in the feminist movement.
The focus is on “Linda is a bank teller” and “Linda is a bank teller and is active in the feminist movement”. Most people will rate “Linda is a bank teller and is active in the feminist movement” as being more probable than “Linda is a bank teller”, despite Linda having to be a bank teller in order to be a feminist bank teller in the first place! The set of all feminist bank tellers is well contained within the set of all feminist bank tellers.
Instead of ranking the probability, most people will recognise the mistake when shown it like this:
Which is more probable?
- Linda is a bank teller.
- Linda is a bank teller and is active in the feminist movement.
Though some people still opt for the latter option. This is because the direct comparison mobilises System 2 to make a comparison. In the first example, each event is judged independently of its surrounding context.
Simpler Questions
Which alternative is more probable?
- Mark has hair.
- Mark has blond hair.
Which alternative is more probable?
- Jane is a teacher.
- Jane is a teacher and walks to work.
These examples don’t trip people up as much, because only irrelevant detail is added. The story or model formed in our heads does not become more plausible or more coherent.
Dinner Sets
Set A:
- 8 dinner plates, all in good condition
- 8 soup/salad bowls, all in good condition
- 8 desert plates, all in good condition
- 8 cups, 2 broken
- 8 saucers, 7 broken
For a total of 40 pieces.
Set B:
- 8 dinner plates, all in good condition
- 8 soup/salad bowls, all in good condition
- 8 desert plates, all in good condition
For a total of 24 pieces.
When doing a joint evalutation – i.e. comparing the two sets side-by-side – it’s easy to see that Set A should be worth more than Set B seeing as it is a superset of Set B with 16 more items (7 of which are intact).
However, when doing in a single evaluation – i.e. comparing the two sets independently without seeing the other one – Set B is rated as being worth more.
Objective Probability
Some critics argue that it’s reasonable to substitute plausibility for probability since it’s difficult to understand what probability really means. This example shows that we do this even when the idea of probaility is objective.
A six-sided die with 4 green faces and 2 red faces is rolled 20 times. Which of the following sequences is most likely?
- RGRRR
- GRGRRR
- GRRRRR
People assume that since there’s too many Rs in the first exmaple for it to be probable and so go with option 2 since it contains an additional G. This is wrong. The probability of a sequence of 5 rolls is higher than a sequence of 6.
Plausibility vs Probability
The conjunction fallacy is sometimes a consequence of substituting plausibility for probability. The idea that Linda is a feminist bank teller seems much more plausible than being a bank teller due to her background, when in reality the probability isn’t as high.
Sum-Like Variables
The conjunction fallacy is also partly due to System 1’s poor ability to deal with sum-like variables. In the Dinner Sets example, people will represent Sets by their norms and prototypes – the “average” piece of dinnerware.
This means that even if you add value, the average perception decreases and so it’s likely to priced as less.
In the example, economic value is a sum-like variable. Probability is also a sum-like variable:
\[P(\text{Linda is a teller}) = P(\text{Linda is a feminist teller}) + P(\text{P is a non-feminist teller})\]This is yet another example of our intuitions failing to follow the strict logical rules of probability.
The sum-like nature of economic value is more obvious than the sum-like nature of probability. The System 1 response to the Linda example is much stronger than the dinnerware response, so it’s harder to overcome our intutitions.
A Failure of System 1 and System 2
In the Linda example, System 1 creates a story that seems likely and it’s the story that informs our decision, rather than logic. However, most people understand the rules of logic that the probability of one event is higher than two mutually exclusive ones. It’s thefore a failure of a lazy System 2, being uncritical about our intutitions.
Causes Trump Statistics
This chapter is about how we intuitively treat different types of base rates:
- Statistical base rates: General facts about the population to which a case or event belongs; underweighted and often neglected all together since it doesn’t help make a good story or mental model.
- Causal base rates: Base rates that are treated as specific information about an individual case and is combined with other-case specific information. These are used more intuitvely because it paints a better picture.
You can have one underlying base rate (such as the fact 85% of cabs are from one company) that can be stated as both a statistical base rate and a causal base rate.
It boils down to the fact that statistical results with a causal interpretation have a stronger effect on our thinking than noncausal information, even when the two should have an identical effect on the resulting probability.
Examples of Causal vs Statiscal Base-Rates
Cab Problem, Statistical
- A cab was involved in a hit-and-run accident at night.
- Two cab compaines, the Green and the Blue, operate in the city.
You are given the following information:
- 85% of the cabs in the city are Green and 15% are Blue.
- A witness who is accurate 80% of the time identified the cab as Blue.
What is the probability that the cab involved was actually Blue?
The common answer is 80% – base rates are neglected entirely. This is because it’s a statistical base rate, general information about the prevelance of certain cabs in the city. As it’s put in the book:
A mind that is hungry for causal stores finds nothing to chew on.
Cab Problem, Casual
- A cab was involved in a hit-and-run accident at night.
- Two cab compaines, the Green and the Blue, operate in the city.
You are given the following information:
- The two companies operate the same number of cabs, but Green cabs are involved in 85% of accidents.
- A witness who is accurate 80% of the time identified the cab as Blue.
The common answer for this one more accurate to the Bayesian estimate of 41%. This is because it tells a better story: you form the stereotype that Greens are reckless drivers and adaquetly incorportate this information.
Exam, Statistical
- A student was selected from a sample in which 75% of students had failed the test.
- Given this (missing) description of a student, what is the chance they passed the test?
There’s no causal story to latch onto here, it just feels like some information about the population as a whole and nothing pertaining to the individual base case.
Exam, Causal
- A random student was selected after an examination in which only 25% has passed.
- Given this (missing) description of a student, what is the chance they passed the test?
Wow! A test only 25% passed… that seems like a difficult test. I better use that information.
Stereotyping
Stereotyping is a consequence of how our minds represent sets. In the first section, [[Thinking, Fast and Slow - Two Systems]]N, the book suggested that we represent things by norms and prototype exemplars.
We think of refridgerators, horses and New York police officers by examples of “normal” versions of these categories. Horses are about this big, New York police officers have this sort of accent and fridges are white on the outside with a yellowly sort of light on the inside.
When the categories that these exemplars describe are social, they are called a stereotype.
It’s part of our culture to reject stereotypes – this is a great idea for many aspects of life like job interviews in order to prevent discrimination and unconcious bias. However, neglecting valid stereotypes will result in sub-optimal judgements.
The stereotype that young male adults are bad drivers is what makes insurance companies all of their money.
The Bystander Effect
There’s a brief foray into the bystander effect in this chapter. The bystander effect states that individuals are less likely to offer help to a victim when there are other people present. This is because individuals fel relieved of responsibility when they know that others have heard the same request for help.
Causes vs Statistics in Teaching Psychology
Teaching psychology concepts has proven difficult because students still don’t take into account many of the effects taught in their own decision making. I’m sure I’ll make the same mistake.
What has shown to be more effective though is using causal examples and demonstrating that the effects work on them too. You are more likely to learn something by finding surprises in your own behavior than by hearing surprising facts about people in general.
Regression to the Mean
Regression to the mean, or the regression fallacy, is the assumption that something returns to normal as a result of corrective actions rather than due to random fluctuations in the value.
Regression Fallacy Examples
Pilots
When pilots are learning to fly, the best way to improve performance is to reward good behaviour rather than to punish bad behaviour. This is supported by evidence from humans, rats, pigeons, loads of animals.
Flight instructors may complain that this is optimal: in actual training, if someone does a good job and they are congratulated, the next time they make the same manoeuvre they are likely to perform worse. This is the opposite to punishment, when someone is berated for a mistake, the next time they make the move they are likely to do a better job.
This is a consequence of the regression fallacy. Good manouevres and poor manouevres are above and below the mean of a neutral manoeuvre. Each individual case is only due to the random fluctuations in the quality of performance. Individuals doing well were probably just lucky on that particular attempt and therefore likely to detoriate since they can fall back down further (not literally). The opposite is true when making a bad attempt, there’s more room to improve and any movement back towards the mean is better.
Golf
One thing that makes sports compelling is how the individual performance of certain athlete varies from day to day. For example, in a hypothetical golf tournament where the average score is par 72:
- Alex does a very good job and finishes with a score of 66.
- Bob does a very poor job and finishes with a score of 77.
Alex’s score is due to a combination of above-average skill and good luck. Bob’s score is probably due to a below-average skill and poor luck. In both cases, the most probable thing for both players to do is to approach the mean. Alex will likely not do as well on day 2, and Bob will likely do better on day 1.
Sports Illustrated Jinx
The idea that an athelete going on the front cover of a sports magazine worsens their performance in the next season is due to a regression. The reason an athelete being on the front cover of a magazine is a good performance and so, as they are likely to regress to the mean, their performance will decrease.
This is also an example of a misguided causual story to explain the effect. People attribute the poor performance afterwards to overconfidence and the pressure of meeting high expectations, but in reality it’s just statistics.
Highly Intelligent Women
Highly intelligent women tend to marry men who are less intelligent than they are.
Causal stories:
- They don’t want to be threatened competitions from a man’s intelligence (sexist)
- Highly-intelligent men don’t want to marry highly-intelligent women.
Actually, it’s just statistics. In general, since the correlation between the intelligence of spouses is less than perfect, highly intelligent women will be on average married to people who are less intelligent than they are.
Depressed Children
Depressed children treated with an energy drink improve significantly over a three-month period.
Depressed children are an extreme group, and their level of depression will regress to the mean over time on average. This is implying that correlation is the same as causation. To prove this for real, you’d need to show that energy drinks improve the happiness of depressed children more than a control group regresses to the mean.
Regressions in Reverse
A good indication of whether there is a causal explanation to explain an improvement is whether it works in reverse. In the sporting examples, if you thought of time going backward, the people who did better on day 2 will likely to worse on day 1 and vice versa.
Correlation Coefficients
A corellation coffiecient is a numerical value that describes the linear correlation between to variables. It spans from $0$ to $1$.
- The correlation coefficient between the height of a parent and the height of a child is $0.5$.
- The correlation coefficient between the size of objects measured in metric or imperial units is $1$.
- The correlation coefficient between height and weight among US adult males is $0.41$.
- The correlation coefficient between SAT scores and GPA is about $0.6$.
- The correlation coefficient between education and income level is $0.4$.
- The correlation coefficient between family income and the last 4 digits of their phone number is $0$.
Inventing Stories
The failure to identify statistics as the explanation for regression to the mean is the result of System 1 playing its usual game of finding coherent stories that explain the evidence which, being an automatic and quick operation, don’t factor important things like the weight of various pieces of evidence or the rules of logic.
Causal stores will be invented when regression is detected, but they will be wrong because the truth is that regression to the mean has an explanation but does not have a cause.
Making Good Predictions
The main problem with how we make intuitive predictions is that we often fail to take into account the quality of evidence and instead base our beliefs on the causal story we can tell. This problem is made worse by things such as intensity matching and heuristics.
Intuitive Decision Making Process
Julie is a senior in a state univeristy. She read fluently when she was four years old. What is her grade point average (GPA)?
- You search for a causal link. Early reading and a high GPA are indicators of academic talent, so the question makes sense. You’d realise if it wasn’t associatively coherent, like “What is the chances she had ketchup on her toast his morning?”. What System 1 doesn’t realise though is the strength of this relationship. Of course there’s some correlation here, but System 1 doesn’t take into account the correlation coefficient. WYSIATI applies here: you don’t even realise your mistake. Your associative machinery just keeps marching on.
- The evidence is compared to its relevant norm. This answers the question “How academic is a child who starts fluently reading at 4? What relative rank or percentile does this put the child in?”.
- The answer to the previous question is intensity matched with her general academic ability, not just that in relation to how young children read.
- The answer is then again intensity matched with a scale of GPA. This is the final answer.
The core issue here is that the strength of the evidence is never considered. Once the causal story is created, the associative machinery eventually settles on the most coherent solution possible.
In reality, regression to the mean postulates that you will often be dissapointed by the medicority of early readers and surprised by the improvement of relatively weak readers.
Prediction Matches Evaluation
The author did a study which asked two sets of questions. A description of a student was given, followed by two sets of questions (one for each group):
How much does this description impress you with respect to academic ability?
What percentage of descriptions of freshmen do you believe would impress you more?
And
What is your estimate of the grade point average that the student will obtain?
What is the percentage of freshmen who obtain a higher GPA?
The two examples assess two seperate things: the former gets the participant to evaluate the current evidence for how the student is doing currently and the latter gets the participant to predict the ultimate outcome in anoither.
One is about description, the other is about the student’s future academic performance.
The judgements, when matched across the scales, were identical from both groups of respondents. This highlights the main flaw: the prediction of the future is not distinguished from an evaluation of current evidence.
This process is guaranteed to generate predictions of outcomes that are systematically biased as they ignore regression to the mean – “nonregressive intuitions”.
A Better Method For Intuitive Predictions
For the GPA example:
- Start with an estimate of average GPA.
- Determine the GPA that matches your impression of the evidence.
- Estimate the correlation between your evidence and GPA.
- If the correlation is $0.3$, move $30\%$ of the distance from the average to the matching GPA.
The value of $0.3$ is an estimated correlation coefficient – a measure of how strong the relationship between early reading and later academic success is.
In the absence of information, your estimate is the average.
With information that fully reflects the outcome, i.e. a correlation coefficient of $1$, your estimate is what you would have predicted originally.
It could be summarised like this:
- Move to the baseline.
- Perform your normal intuitive intuition that matches your impression.
- Determine the strength of the relationship.
- Move from the baseline to your intuitive prediction using the strength of the evidence.
This approach builds on your inutition but moderates it and regresses it towards the mean. The predictions are only as extreme as the evidence.
Continious vs Discrete Predictions
GPA is a sliding scale that can take on pretty much any value in a range. Sometimes, like with the Representativeness Heuristic affecting a judgement of the likelihood of discrete outcomes, you need to adjust your intuitions in the same way.
Bob the trumpet player is an example of a prediction with a discrete number of outcomes. You are trying to find out which outcome is more likely, there are exactly two possible scenarios.
The two types of correction intuition are similar:
You make an intutive prediction, adjust it in relation to some base rate or average outcome and go with that. This scales your intuitive response.
Maybe Don’t Correct Your Intuitions
Correcting intuitive predictions is effortful (primarily a System 2 activity). This is a good idea when the stakes are high and you don’t want to make mistakes, but can get in the way some of the times.
Corrected intuitive predictions aren’t fun. They only allow you to predict rare or extreme events when the evidence is very good. A teacher won’t be able to say “I thought so!” in seeing one of their students become super successful or a venture capatilist will miss the opportunity to invest in the next Facebook or Google. It balances risk, and sometimes risk is fun.
Most of the time, these biased intuitions are fine. There’s no point analysing every single decision, heuristics are useful because they work most of the time. Otherwise they wouldn’t exist.
The main thing to take away is to think about how much you know when making a decision.