Notes - ADS HT24, Red-black trees

What are the the 5 properties of red-black trees?

Every node is either red or black
The root is black
Every leaf (which is always NIL) is black
If a node is red, both its children are black
For every node, all simple paths from $x$ to descendant leaves have the same number of black nodes (excluding $x$)

Suppose $x$ is a node in a red-black tree. What is bh($x$), and why is this well-defined?

The number of black nodes in any simple path from $x$ to descendant leaves, excluding $x$.
Well-defined since one of the properties of a red-black tree is that this number is the same for all paths.

Quickly prove that a red-black tree $T$ with $n$ items (not including NIL leaves) has a height $\le 2 \log(n + 1)$.

First, note that height($T$) $\le 2$bh($T$) since for an arbitrary path $P$ from root to a leaf, the number of red nodes in $P$ is less than the number of black nodes in $P$.
Then, note that bh($T$) $\le \log(n+1)$ since if we collapse every red node to its black parent, the resulting tree has height bh(T). Every node has $\ge 2$ children, but the number of leaves is still the same as the number of leaves in $T$, which is $n + 1$. So $2^{\text{bh}(T)} \le n + 1$, which implies bh($T$) $\le \log(n + 1)$.

The approach for implementing insertion in red-black trees to insert a node $x$ like normal and then fix any violations to the red-black tree properties that we might have created. What type of violation might we create?

A red-red violation between $x$ and its parent.

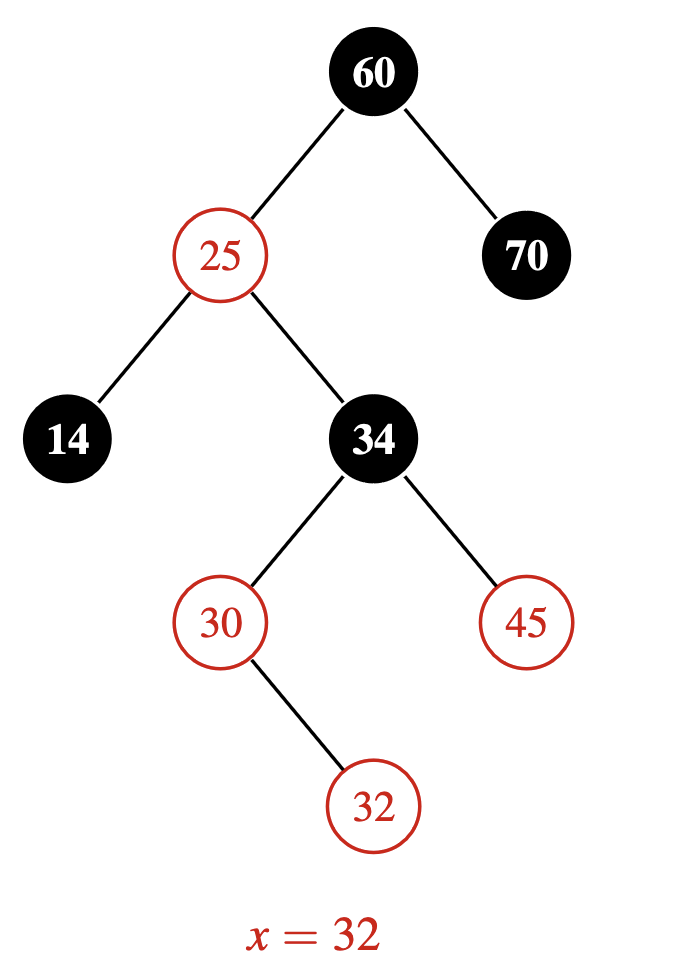
Suppose we have just inserted $x = 32$ into the red-black tree above and have created a red-red violation. What do you call this case, and what approach do we take here to move the violation upwards?

The “funky uncle”. Recolour $p[x]$ and $\text{uncle}[x]$ black, and recolour $p[p[x]] = \text{grandparent}[x]$ red.

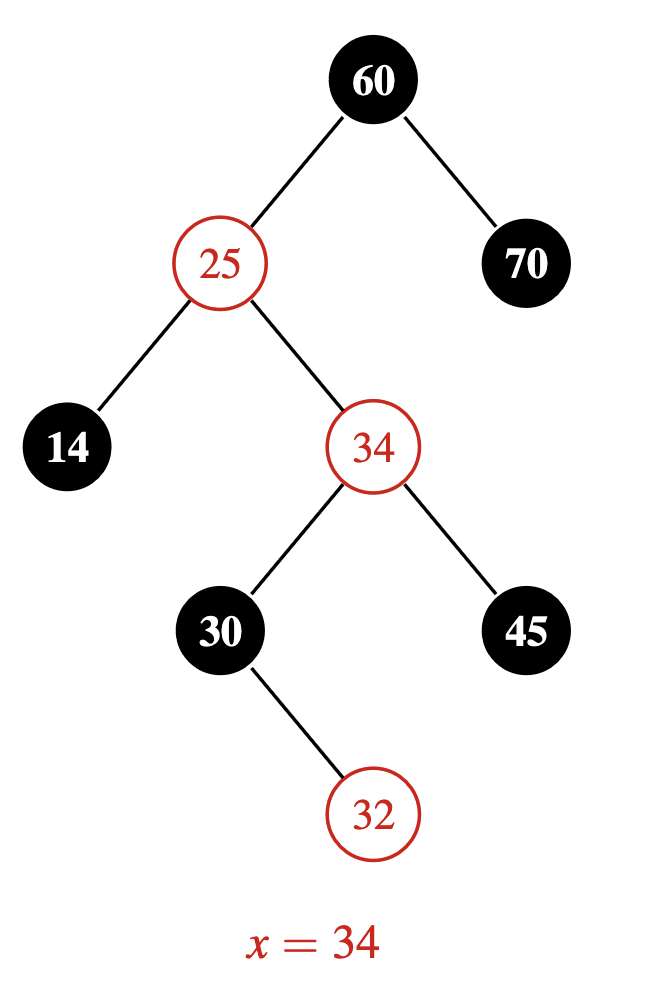
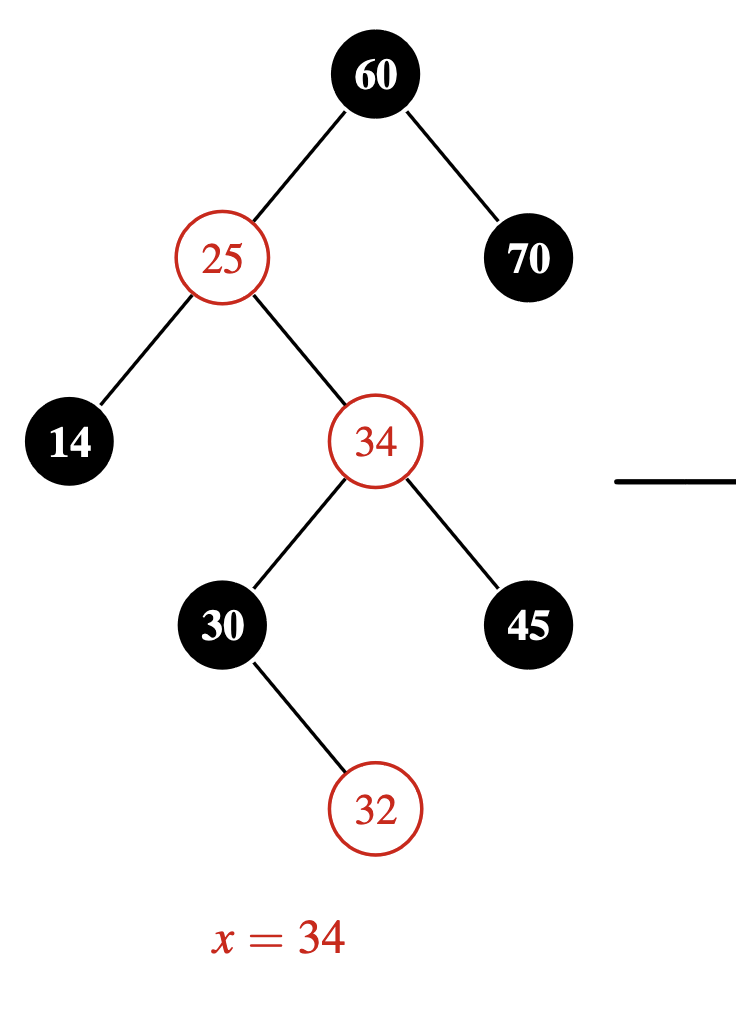
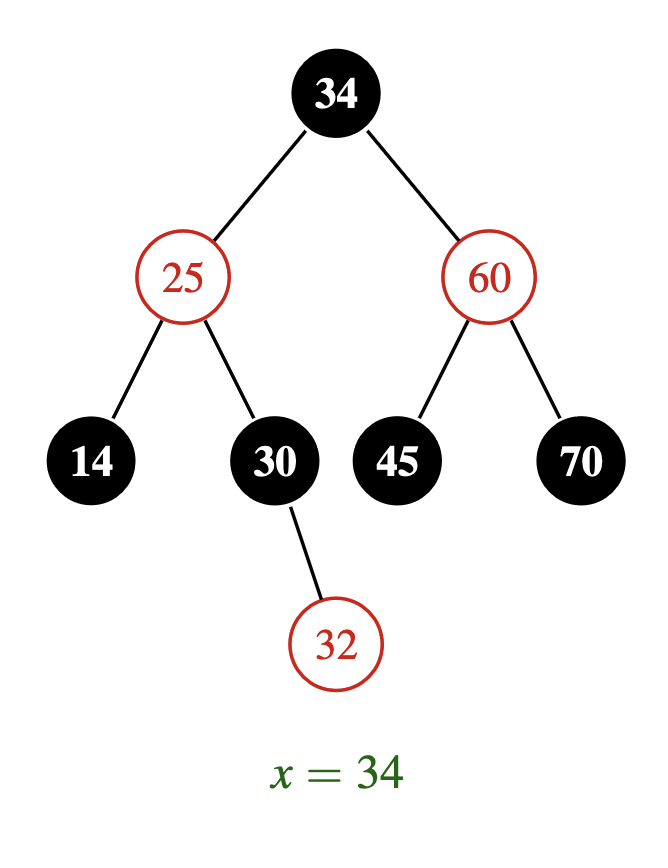
We’re in the process of fixing a violation after inserting $32$ into a red-black tree. Here we are now focussed on fixing the red-red violation between $x = 34$ and $p[x] = 25$. What do you call this case, and what do you do to move the violation upwards?

This is the “zig-zag” case, since $x$, $p[x]$ and $p[p[x]]$ form a zig-zag shape. Here you rotate $x$ with $p[x]$ to form

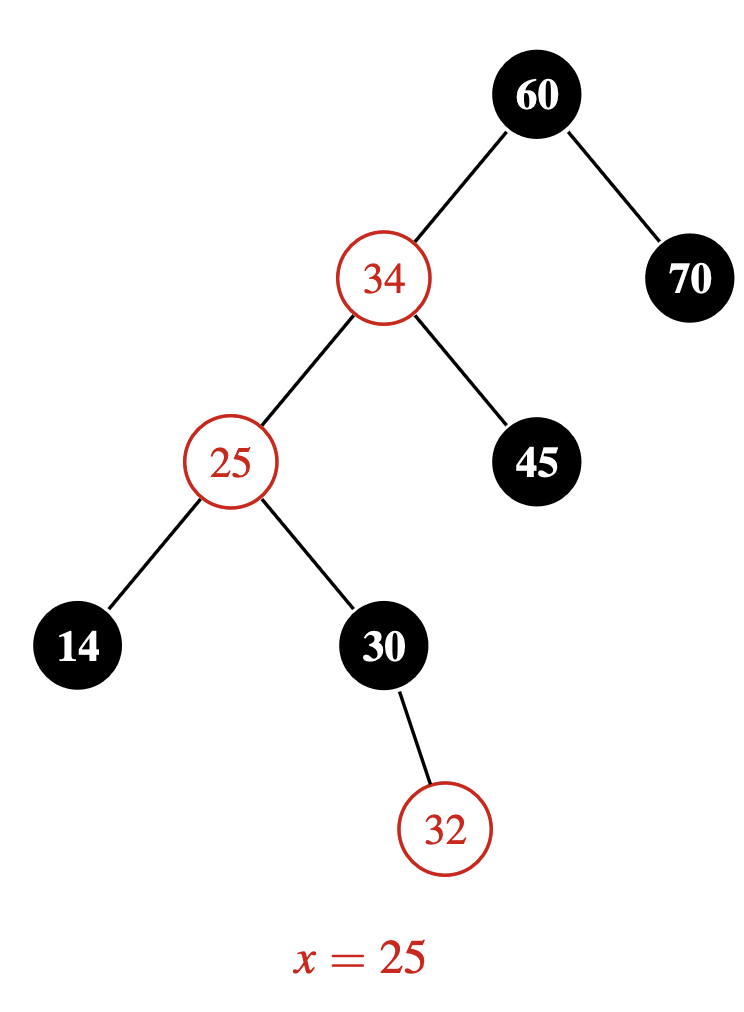
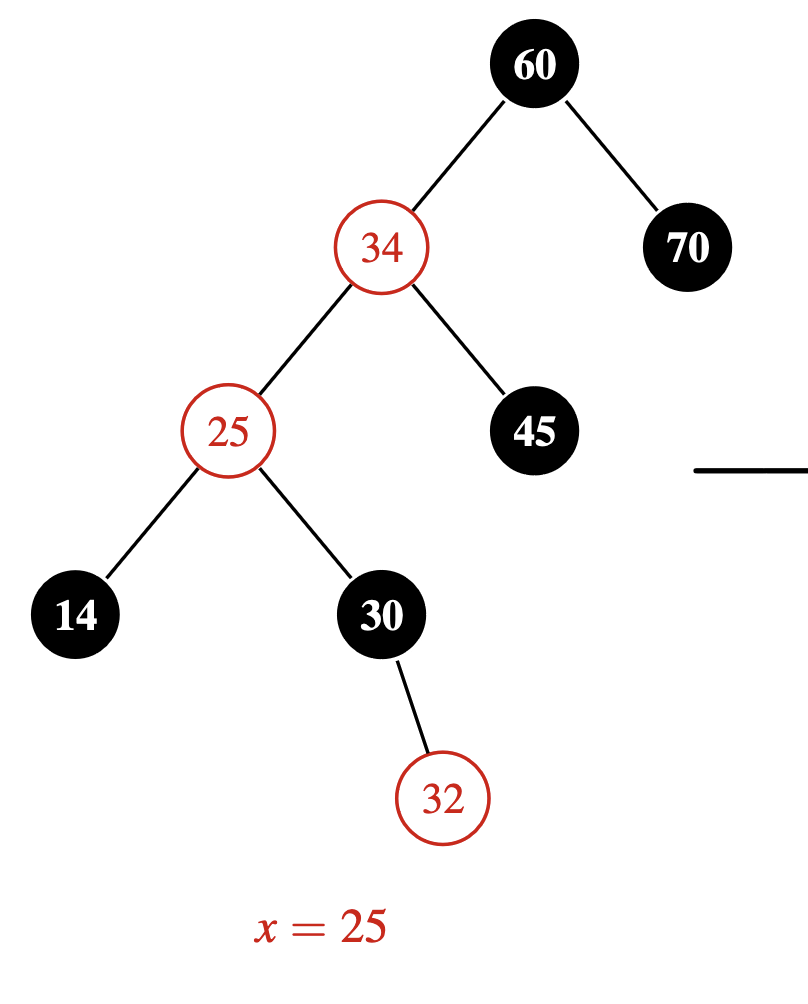
We’re in the process of fixing a violation after inserting $32$ into a red-black tree. Here we are now focussed on fixing the red-red violation between $x = 25$ and $p[x] = 34$. What do you call this case, and what do you do to move the violation upwards?

This is the zig-zig case, since $25, 34$ and $60$ form a straight line. This you fix by switching the colours of $p[x]$ and $p[p[x]]$ and then rotating $p[x]$ with $p[p[x]]$.

What are the three cases that might occur when fixing violations in a red-black tree (just the names).

Funky uncle
Zig-zag
Zig-zig

Give the pseudocode for $\text{RBInsert}(T, x)$, which inserts a value $x$ into a red-black tree. You can use Insert($T$, $x$) for normal binary search trees as a subroutine, and for each of the three cases in the main loop, don’t go into too much detail but briefly describe how you’d “move the violation upwards”.

RB-INSERT(T, x):
	INSERT(T, x)
	colour[x] = red

	while x != root(T) and colour[x] = colour[p[x]] = red:
		y = uncle[x]
		
		if colour[y] = red:
			# the "funky uncle case"
			keep x red
			recolour p[x] and uncle[x] black
			# now violation is between p[x] and p[p[x]]
			
		else:
			if x - p[x] - p[p[x]] is not aligned:
				# the "zig-zag case"
				rotate x with p[x]
				
			else if x - p[x] - p[p[x]] is aligned:
				# the "zig-zig" case
				rotate p[x] with p[p[x]]
				recolour p[p[x]] black (was originally p[x])
				recolour p[x] red

	colour[root[T]] = black

The pseudocode for inserting an element into a red-black tree is as follows:

RB-INSERT(T, x):
	INSERT(T, x)
	colour[x] = red

	while x != root(T) and colour[x] = colour[p[x]] = red:
		y = uncle[x]
		
		if colour[y] = red:
			# the "funky uncle case" (case 1)
			keep x red
			recolour p[x] and uncle[x] black
			# now violation is between p[x] and p[p[x]]
			
		else:
			if x - p[x] - p[p[x]] is not aligned:
				# the "zig-zag case" (case 2)
				rotate x with p[x]
				# this reduces it to case 3
				
			else if x - p[x] - p[p[x]] is aligned:
				# the "zig-zig" case (case 3)
				recolour p[x] black
				recolour p[p[x]] red
				rotate p[x] with p[p[x]]
				# this terminates the algorithm
				 

	colour[root[T]] = black

Quickly prove that this algorithm terminates, and in fact does so in $O(\log n)$ iterations of the while loop.

It helps to draw a picture of each case:

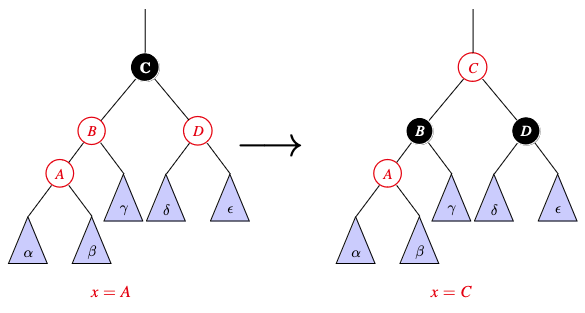
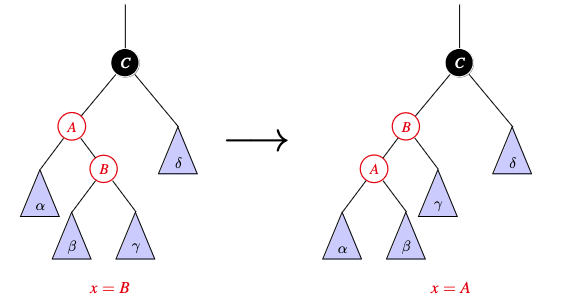
Note that:

Case 1 propogates the red-red violation further up the tree
Case 2 converts the tree into one with case 3
Case 3 ends the algorithm, as there is no longer a red-red violation.

Hence the worst case is if case 1 is repeated over and over. Since a red-black tree with $n$ items has height $O(\log n)$, this case can only occur $\log n$ times, and so the algorithm must terminate after $O(\log n)$ steps.

Draw the “funky uncle” case of insertion a red-black tree and then describe and draw the fix.

Invert the colours of $p[x], \text{uncle}[x], \text{grandparent}[x]$

Draw the “zig-zag” case of insertion into a red-black tree and then describe and draw the fix.

Rotate $x$ with $p[x]$.
(Note this doesn’t move )

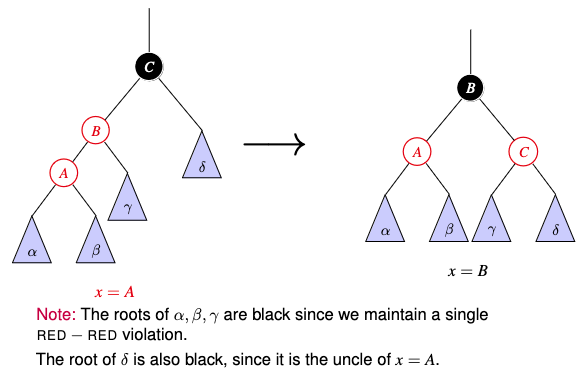
Draw the “zig-zig” case of insertion into a red-black tree and then describe and draw the fix.

Rotate $p[x]$ with $\text{grandparent}[x]$ and recolour.

Assuming that we’re considering a chain of nodes $x$, $y$, $z$ decreasing in depth in a binary tree, complete the following table for how splay trees / red-black trees handle different cases in their algorithms.

Case (down) / Alg (across)	Splay trees	Red-black trees
Funky uncle	…	…
Zig zig	…	…
Zig zag	…	…

For the specific case of red-black trees, also highlight how each case affects how “close we are” to fixing the red-red violation.

In splay trees, we are interested in moving the element we’re splaying up through the tree. In red-black trees, we are interested in fixing a the red-red conflict.

Case (down) / Alg (across)	Splay trees	Red-black trees
Funky uncle	N/A	Recolour, red-red conflict has moved upwards
Zig zig	Rotate yz, then xy	Rotate yz, recolour, we are done
Zig zag	Rotate xy, then xz	Rotate xy, reduces to zig zig

We have the following partial table of what steps to perform in either a splay tree or a red-black tree in any given situation:

Case (down) / Alg (across)	Splay trees	Red-black trees
Funky uncle	N/A	Recolour, red-red conflict has moved upwards
Zig zig	Rotate yz, then xy	…
Zig zag	Rotate xy, then xz	…

Given the description of the steps that need to be performed for the splay tree, what’s an easy way to remember the steps that need to be performed for red-black trees?

It’s the first rotation and then a recolour, so:

Zig-zig: rotate yz
Zig-zag: rotate xy

In red-black trees, how can you remember whether to recolour the nodes in the zig-zig or zig-zag steps?

Rotate, recolour any nodes in order to fix the violation, and then make sure the black height is still the same.

Notes - ADS HT24, Red-black trees

Flashcards

Proofs

Related posts