Notes - ADS HT24, Splay trees
Flashcards
Suppose:
- $S = \{x _ 1, x _ 2, \ldots, x _ n\}$ is the set of values in a BST
- $p _ i$ is the probability that item $x _ i$ is accessed in a sequence of $m$ searches
Can you define the statically optimal BST $T^\star$?
$T^\star$ is the binary tree with minimum aggregate look-up cost.
Can you give the pseudocode for Splay($x$), which moves $x$ to the root of a BST through a sequence of rotations?
SPLAY(x):
while x is not the root:
y = p[x]
if y is the root
rotate x and p[x]
else:
z = p[y]
if x - y - z is aligned: (zig-zig)
rotate y with z
rotate x with y
else x - y - z is not aligned: (zig-zag)
rotate x with y
rotate x with z
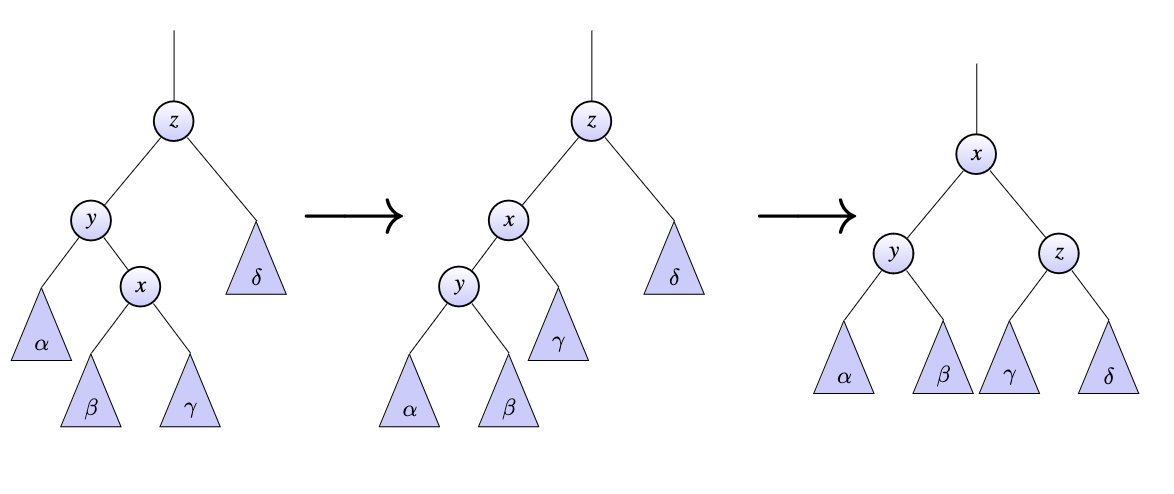
Suppose:
- We are splaying a node $x$ in a splay tree
- We are in the “zig-zag” case, i.e. if $y$ is $x$’s parent, and $z$ is y’s parent, then $y < x < z$ (or the other way around)
Can you:
- Describe the sequence of rotations that are used to move $x$ closer to the root
- Highlight a mneumonic that makes remembering this easier
- Draw a picture representing these
- Rotate $x$ with $y$, and then $x$ with $z$
- “Zig-zag preserves kinked splays” (also $xyxz$ looks kind of zig-zaggy)
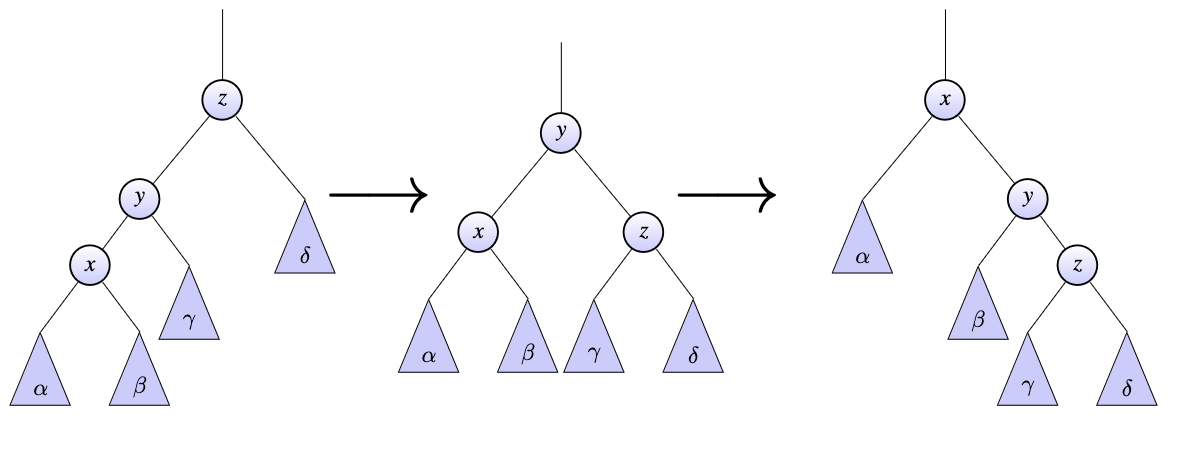
Suppose:
- We are splaying a node $x$ in a splay tree
- We are in the “zig-zig” case, i.e. if $y$ is $x$’s parent, and $z$ is y’s parent, then $x < y < z$ (or the other way around)
Can you:
- Describe the sequence of rotations that are used to move $x$ closer to the root
- Highlight a mneumonic that makes remembering this easier
- Draw a picture representing these
- Rotate $y$ with $z$, then rotate $x$ with $y$
- “Zig-zig preserves straight splays”
Give the pseudocode for the implementation of Insert($x$) in a splay tree (this is quite short).
INSERT(x):
INSERT_BST(x) # insert in the normal BST way
SPLAY(x)
What are the four high level steps in implementing Delete($x$) in a splay tree?
- First Splay($x$)
- Remove $x$ from the root, this splits into two trees $T _ {<x}$ and $T _ {>x}$.
- Let $w = \text{Max}(T _ {<x}$), then Splay($T _ {<x}$, w)
- Join $T _ {<x}$ and $T _ {>x}$ on $w$
Since red-black trees are balanced binary search trees, they have amotised lookup cost $O(\log n)$. In this case, why are splay trees useful? Define a metric and state a bound which makes their usefulness clear.
They are not neccesarily optimal for arbitrary access sequences, e.g. requesting a leaf over and over will have cost $O(\log n)$. Splay trees adapt to access sequences.
To measure this, we can compare them to statically optimal trees.
Suppose $S = \{x _ 1, \cdots, x _ n\}$ is the set of values in a BST. Suppose that in a sequence of $m$ searches, value $x _ i$ is accessed $mp _ i$ times for $i = 1, \cdots, n$, where:
- $p _ i$ is the frequency that item $i$ is accessed
- $p _ 1 + \cdots + p _ n = 1$
- The look up cost of item $x _ i$ is $1 + \text{depth}(x _ i)$.
Let $T^\star$ be the “statically optimal binary search tree”, i.e. the BST with minimum aggregate lookup cost. Then
\[\text{cost}(T_\text{splay}) = O(\text{cost}(T^\star))\]What is a statically optimal binary search tree $T^\star$?
Suppose $S = \{x _ 1, \cdots, x _ n\}$ is the set of values in a BST. Suppose that in a sequence of $m$ searches, value $x _ i$ is accessed $mp _ i$ times for $i = 1, \cdots, n$, where:
- $p _ i$ is the frequency that item $i$ is accessed
- $p _ 1 + \cdots + p _ n = 1$
- The look up cost of item $x _ i$ is $1 + \text{depth}(x _ i)$.
Then for an arbitrary binary search tree $T$ over these items,
\[\text{cost}(T) = m \sum_{i=1}^n p_i(1 + d_i)\]Let $T^\star$ be the BST with minimum aggregate lookup cost. Then
\[\text{cost}(T_\text{splay}) = O(\text{cost}(T^\star))\]Suppose:
- $S = \{x _ 1, \cdots, x _ n\}$ is the set of values in a BST.
- In a sequence of $m$ searches, value $x _ i$ is accessed $mp _ i$ times for $i = 1, \cdots, n$, where:
- $p _ i$ is the frequency that item $i$ is accessed
- $p _ 1 + \cdots + p _ n = 1$
- The look up cost of item $x _ i$ is $1 + \text{depth}(x _ i)$.
For any binary search tree $T$ for these items, what is $\text{cost}(T)$?
- $p _ i$ is the frequency that item $i$ is accessed
- $p _ 1 + \cdots + p _ n = 1$
In the amortised analysis of splay trees, our overall goal is to show that the cost of a single splay operation (where cost is measured as the number of rotations) is bounded by
\[O(\log n)\]
To do this, we prove the “access lemma”. Can you state this, and then quickly describe why this implies the result we want?
Make the following definitions:
- $T$ is the tree under consideration
- $\text{size}(x) = \text{number of nodes in }x\text{‘s subtree}$
- $\text{rank}(x) = \log \text{size}(x)$ (or $r(x)$ for shorthand)
- $\Phi(T) = \sum _ {x \in T} \text{rank}(x)$ (the potential function used in this context)
Then the access lemma says that if $\text{rank}(x)$ and $\text{rank}’(x)$ are the ranks of $x$ before and after the splay operation, then
\[\text{total charge of splay} \le 1 + 3(r'(x) - r(x))\]This implies the result we want because the maximum rank is $\log n$, and the minimum rank is $0$, so
\[\begin{aligned} \text{total cost of splay} &= \text{total charge of splay} \\\\ &= O(\log n) \end{aligned}\]In the amortised analysis of splay trees, our overall goal is to show that the cost of a single splay operation (where cost is measured as the number of rotations) is bounded by
\[O(\log n)\]
To do this, we prove the “access lemma”, which states that if we have the definition
- $T$ is the tree under consideration
- $\text{size}(x) = \text{number of nodes in }x\text{‘s subtree}$
- $\text{rank}(x) = \log \text{size}(x)$ (or $r(x)$ for shorthand)
- $\Phi(T) = \sum _ {x \in T} \text{rank}(x)$ (the potential function used in this context)
- $\text{rank}(x)$ and $\text{rank}’(x)$ are the ranks of $x$ before and after the splay operation (note that $r’(x)$ is the rank at the root)
Then
\[\text{total charge of splay} \le 1 + 3(r'(x) - r(x))\]
This implies the result we want because the maximum rank is $\log n$, and the minimum rank is $0$, so
\[\begin{aligned}
\text{total cost of splay} &\le \text{total charge of splay} \\\\
&= O(\log n)
\end{aligned}\]
Quickly prove this.
In all cases, let $x$ be the node under consideration, $y$ its parent, and $z$ its grandparent. We want to show that the charge $\hat c _ i := c _ i + \Delta \Phi$ at each elementary splay step is bounded by an appropriate factor, so that eventually we see that
\[\begin{aligned} \text{total cost of splay} &\le \text{total charge of splay} \\\\ &= \sum \hat c_i \\\\ &\le 1 + 3(r'(x) - r(x)) \\\\ \end{aligned}\]There are 3 types of elementary splay operation: a rotation at the root, a zig-zig, or a zig-zag.
Charge of rotation at the root:
\[\begin{aligned} \hat c_i &= c_i + \Delta \Phi \\\\ &= 1 + \Delta \Phi \\\\ &= 1 + r'(x) + r'(y) - r(x) - r(y) \\\\ &= 1 + r'(y) - r(x) \\\\ &\le 1 + r'(x) - r(x) \\\\ \end{aligned}\]Some explanatory notes:
- The $1$ at the beginning comes from the fact that we perform just one rotation, so the actual cost $c _ i$ is $1$
- In the last equality, we use $r(y) = r’(x)$
- In the inequality, we use the fact that $r’(x) \ge r’(y)$, this follows from the fact $x$ is the parent of $y$
Charge of zig-zig step:
\[\begin{aligned} \hat c_i &= 2 + r'(x) + r'(y) + r'(z) - r(x) - r(y) - r(z) \\\\ &= 2 + r'(y) + r'(z) - r(y) - r(x) \\\\ &\le 2 + r'(z) + r'(x) - r(x) - r(x) \\\\ &= 2 + r'(z) + r'(x) - 2r(x) \\\\ &\le 2 + 3(r'(x) - r(x)) - 2 \\\\ &= 3(r'(x) - r(x)) \end{aligned}\]Notes:
- Now we have $2$ since we have $2$ rotations
- In the second equality, we use $r’(x) = r(p)$
- In the first inequality, we use $r(x)<r(y)$ and $r’(x)>r’(p)$
- In the second inequality, we use the convexity of $\log$ (?? don’t really understand this)
Charge of zig-zag step:
\[\begin{aligned} \hat c_i &= 2 + r'(x) + r'(y) + r'(z) - r(x) - r(y) - r(z) \\\\ &\le 2 + r'(y) + r'(z) - r(x) - r(y) \\\\ &\le 2 + 3(r'(x) - r(x)) - 2 \\\\ &= 3(r'(x) - r(x)) \end{aligned}\]Notes:
- In the first inequlaity we use the fact that $r’(x)=r(z)$ and $r(x)<r(y)$.
- In the second inequality we again use the convexity of $\log$.
Overall: Now we need to work out the total charge for the splay operation, which was given above:
\[\begin{aligned} \text{total cost of splay} &\le \text{total charge of splay} \\\\ &= \sum \hat c_i \\\\ &\le 1 + 3(r'(x) - r(x)) \\\\ \end{aligned}\]where the intermediate terms in the sum cancel.
In the amortised analysis of splay trees, our overall goal is to show that the cost of a single splay operation (where cost is measured as the number of rotations) is bounded by
\[O(\log n)\]
To do this, we prove the “access lemma”, which states that if we have the definition
- $T$ is the tree under consideration
- $\text{size}(x) = \text{number of nodes in }x\text{‘s subtree}$
- $\text{rank}(x) = \log \text{size}(x)$ (or $r(x)$ for shorthand)
- $\Phi(T) = \sum _ {x \in T} \text{rank}(x)$ (the potential function used in this context)
- $\text{rank}(x)$ and $\text{rank}’(x)$ are the ranks of $x$ before and after the splay operation (note that $r’(x)$ is the rank at the root)
Then
\[\text{total charge of splay} \le 1 + 3(r'(x) - r(x))\]
This implies the result we want because the maximum rank is $\log n$, and the minimum rank is $0$, so
\[\begin{aligned}
\text{total cost of splay} &\le \text{total charge of splay} \\\\
&= O(\log n)
\end{aligned}\]
This result can actually be strengthened to something called the “general access lemma” or “weighted access lemma”.
- How is this different?
- How is the normal access lemma a special case of this?
- What’s the high-level strategy for proving this?
We introduce arbitrary “weights” $w _ 1, \cdots, w _ n > 0$ and define
- $\text{size}(x) = \sum _ {x _ i \in T _ x} w _ i$
- $W = w _ 1 + \cdots + w _ n$
Then
\[\text{total charge of splay} \le 1 + 3(\log W - \log w_x)\]The standard access lemma is the case where $w _ i = 1$ for all $i$.
The high level strategy for proving this is that we can use an idential proof to the standard access lemma.
Suppose:
- $S = \{x _ 1, \cdots, x _ n\}$ is the set of values in a BST.
- In a sequence of $m$ searches, value $x _ i$ is accessed $mp _ i$ times for $i = 1, \cdots, n$, where:
- $p _ i$ is the frequency that item $i$ is accessed
- $p _ 1 + \cdots + p _ n = 1$
- The look up cost of item $x _ i$ is $1 + \text{depth}(x _ i)$.
- Every item is accessed at least once.
Let $T _ \text{splay}$ be the splay tree for this data. Can you:
- Give an expression for $\text{cost}(T _ \text{splay})$?
- Quickly prove this, using the general access lemma.
For reference, the general access lemma states that:
\[\text{total charge of splay} \le 1 + 3(\log W - \log w_x)\]
For arbitrary “weights” $w _ 1, \cdots, w _ n > 0$ and
- $\text{size}(x) = \sum _ {x _ i \in T _ x} w _ i$
- $\text{rank}(x) = \log \text{size}(x)$
- $W = w _ 1 + \cdots + w _ n$
- $p _ i$ is the frequency that item $i$ is accessed
- $p _ 1 + \cdots + p _ n = 1$
where
\[H := - \sum_{i = 1}^n p_i \log p_i\]To prove this, apply the general acess lemma with $w _ i = p _ i$. Then
\[\begin{aligned} \text{total charge for item }i &\le m p_i (1 + 3(\log(1) - \log p_i) \\\\ &= m p_i (1 - 3\log p_i) \end{aligned}\]Summing over $i$ gives the desired bound.
Suppose:
- $S = \{x _ 1, \cdots, x _ n\}$ is the set of values in a BST.
- In a sequence of $m$ searches, value $x _ i$ is accessed $mp _ i$ times for $i = 1, \cdots, n$, where:
- $p _ i$ is the frequency that item $i$ is accessed
- $p _ 1 + \cdots + p _ n = 1$
- The look up cost of item $x _ i$ is $1 + \text{depth}(x _ i)$
- Every item is accessed at least once
Let $T^\star$ be the statically optimal BST for these items, and let $T _ \text{splay}$ be the splay tree for this data. Can you:
- Relate the cost of $T _ \text{splay}$ and $T^\star$
- Quickly prove this, using the general access lemma.
- $p _ i$ is the frequency that item $i$ is accessed
- $p _ 1 + \cdots + p _ n = 1$
To prove this, apply the general access lemma with $w _ i = 3^{-d _ i}$. Since the tree is binary
\[\begin{aligned} W &= \sum_{i = 1}^n w_i \\\\ &\le \sum^\infty_{j = 0} 2^j 3^{-j} \\\\ &= \sum^\infty_{j = 0} \left(\frac{2}{3}\right)^j \\\\ &= \frac{1}{1 - \frac 2 3} \\\\ &= 3 \end{aligned}\]Then
\[\begin{aligned} \text{total charge for item }i &\le 1 + 3(\log 3 - \log 3^{-d_i}) \\\\ &\le 8(1 + d_i) \end{aligned}\]This is within a constant factor from the cost per access of item $i$ in $T^\star$.