Quantum Information HT24, Grover's algorithm
Flashcards
Suppose
\[f(x) = \begin{cases}
1 &\text{if } x \text{ satisfies some property} \\\\
0 &\text{ otherwise}
\end{cases}\]
This is the classical oracle for a search problem. How is the quantum oracle defined?
Suppose we have a classical oracle that evaluates a boolean function $f : \{0, \cdots, N-1\} \to \{0, 1\}$, and the corresponding quantum oracle defined by
\[U_f\big( |x\rangle \otimes |y\rangle \big) := |x\rangle \otimes |y \oplus f(x) \rangle\]
What is the query complexity of finding some $x$ where $f(x) = 1$ in the classical case, and in the quantum case?
- Classical case: require $\Theta(N)$ queries
- Quantum case: require only $\Theta(\sqrt N)$ queries
Suppose we have a boolean function $f : \{0, \cdots, N - 1\} \to \{0, 1\}$ and want to determine $x$ such that $f(x) = 1$ given a reduced quantum oracle $V _ f$ defined by
\[V_f | x\rangle := (-1)^{f(x)} |x\rangle \quad \forall x \in \\{0, \cdots, N-1\\}\]
Furthermore, suppose the number of $x$ such that $f(x) = 1$ is $S \ll N$. In this context, describe the steps in Grover’s search algorithm, and give a lower bound on the probability that the measurement outcome is a solution.
- Prepare the system in the Fourier basis state $e _ 0 = \frac{1}{\sqrt N} \sum^{N-1} _ {x = 0} \vert x\rangle$
- Apply the reduced oracle $V _ f$
- Apply the gate $W := 2 \vert e _ 0\rangle \langle e _ 0 \vert - I$
- Repeat steps 2 and 3 $K$ times, where $K$ is the closest integer to $\frac \pi 4 \sqrt{\frac N S} - \frac 1 2$.
- Measure the system in the computational basis
With probability at least $1 - S/N$, the measurement outcome will be a solution.
Suppose we have a boolean function $f : \{0, \cdots, N - 1\} \to \{0, 1\}$ and want to determine $x$ such that $f(x) = 1$ given a reduced quantum oracle $V _ f$ defined by
\[V_f | x\rangle := (-1)^{f(x)} |x\rangle \quad \forall x \in \\{0, \cdots, N-1\\}\]
Furthermore, suppose the number of $x$ such that $f(x) = 1$ is $S \ll N$. In this context, Grover’s search algorithm is given by
- Prepare the system in the Fourier basis state $e _ 0 = \frac{1}{\sqrt N} \sum^{N-1} _ {x = 0} \vert x\rangle$
- Apply the reduced oracle $V _ f$
- Apply the gate $W := 2 \vert e _ 0\rangle \langle e _ 0 \vert - I$
- Repeat steps 2 and 3 $K$ times, where $K$ is the closest integer to $\frac \pi 4 \sqrt{\frac N S} - \frac 1 2$.
- Measure the system in the computational basis
Quickly prove that the probability of the outcome of the measurement being a solution is at least $1 - S/N$.
- Prepare the system in the Fourier basis state $e _ 0 = \frac{1}{\sqrt N} \sum^{N-1} _ {x = 0} \vert x\rangle$
- Apply the reduced oracle $V _ f$
- Apply the gate $W := 2 \vert e _ 0\rangle \langle e _ 0 \vert - I$
- Repeat steps 2 and 3 $K$ times, where $K$ is the closest integer to $\frac \pi 4 \sqrt{\frac N S} - \frac 1 2$.
- Measure the system in the computational basis
Write the Fourier basis state
\[|e_0\rangle = \frac{1}{\sqrt N} \sum^{N-1}_{x = 0} |x\rangle\]as
\[|e_0\rangle = \frac{\sqrt{N-S} }{\sqrt N} |\phi_ 0\rangle + \frac{\sqrt S}{\sqrt N} |\phi_ 1 \rangle\]where
\[|\phi_ 0\rangle = \frac{1}{\sqrt{N-S} } \sum_ {x \text{ s.t. } f(x) = 0} |x\rangle\]and
\[|\phi_ 1\rangle = \frac{1}{\sqrt S} \sum_ {x \text{ s.t. }f(x) = 1} |x\rangle\]i.e. splitting the Fourier basis state into the superposition of states that aren’t solutions ($ \vert \phi _ 0\rangle$), and states that do ($ \vert \phi _ 1\rangle$).
Then, parameterising by $\cos \theta = \sqrt{\frac{N-S}{N}\,} = \sqrt{1 - \frac S N}$, $\sin \theta = \sqrt{\frac S N}$, we have
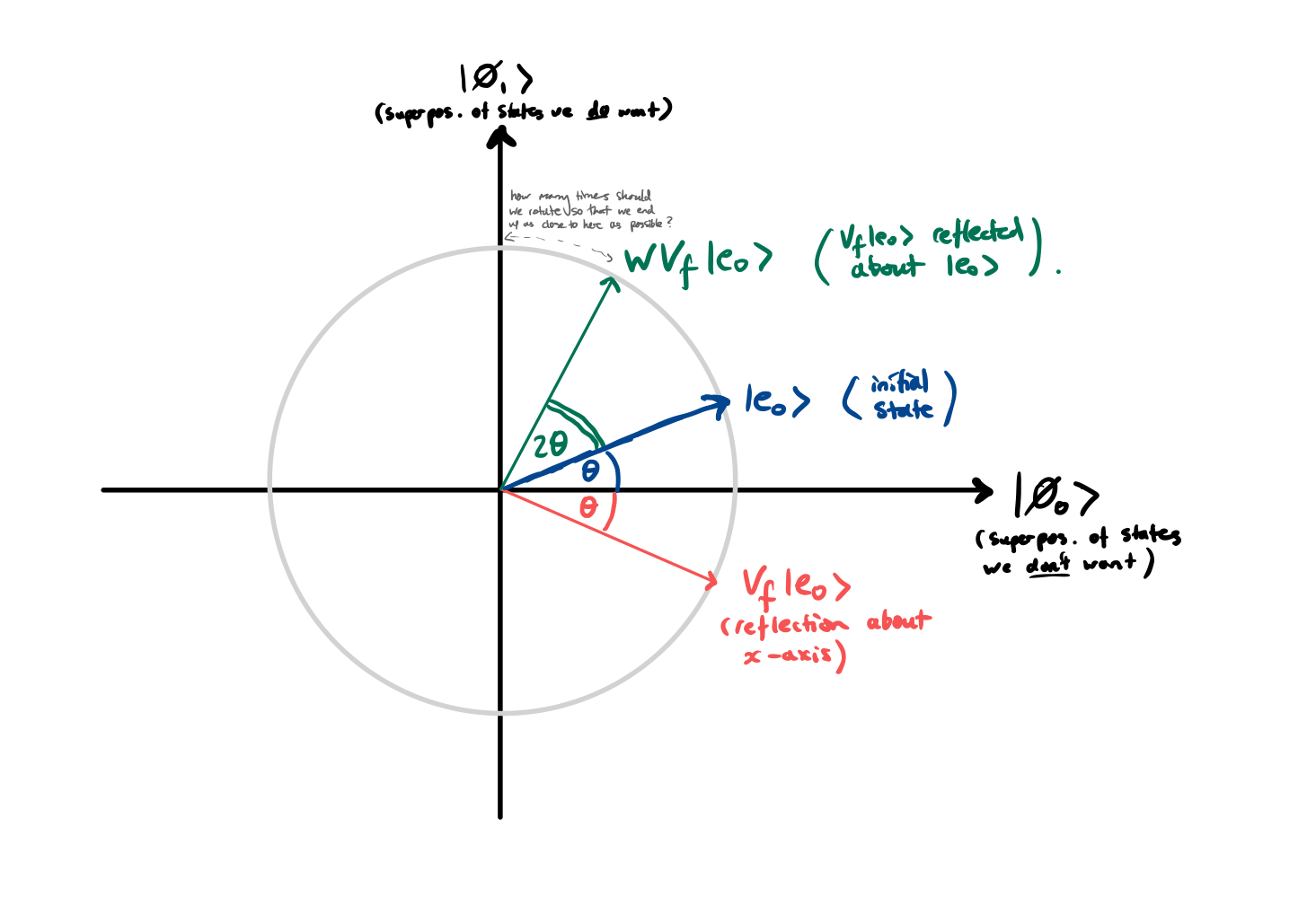
\[|e_0 \rangle = \cos \theta |\phi_0\rangle + \sin \theta |\phi_1\rangle\]Hence we can identify $ \vert e _ 0\rangle$ with the vector $(\cos \theta, \sin \theta)^\top$.
Repeating steps 2 and 3 $K$ times is equivalent to calculating
\[(WV_f)^K |e_0\rangle\]We claim that $WV _ f$ is actually a rotation of $2\theta$ anticlockwise, when $ \vert e _ 0\rangle$ is viewed as the vector $(\cos \theta, \sin \theta)^\top$. This is because $V _ f \vert e _ 0\rangle = \cos\theta \vert \phi _ 0\rangle - \sin \theta \vert \phi _ 1\rangle$ since
\[V_f |x\rangle = \begin{cases} -|x\rangle &\text{if } f(x) = 1 \\\\ |x\rangle &\text{if } f(x) = 0 \end{cases}\]Hence $V _ f$ is actually a reflection about the $x$-axis, or equivalently a rotation of $\theta$ clockwise. But then $W$ is a reflection around $ \vert e _ 0\rangle$, so $WV _ f \vert e _ 0\rangle$ is a rotation of $2\theta$ anticlockwise. Hence
\[(WV_f)^K |e_0\rangle = \cos\big((2K+1)\theta\big) |\phi_0\rangle + \sin \big((2K+1)\theta\big) |\phi_1\rangle\]This is called amplitude amplification, because we are pushing $ \vert e _ 0\rangle$ closer and closer to the $y$-axis by repeated rotation.
Hence then
\[\begin{aligned} p(x \mid x \text{ solution}) &= \left|\langle x|(WV_f)^K|e_0\rangle\right|^2 \\\\ &= |\text{cos}\big((2K+1)\theta\big)\langle x |\phi_0\rangle + \sin \big((2K+1)\theta\big)\langle x|\phi_1\rangle|^2 \\\\ &= \sin((2K+1)\theta)^2 / S \end{aligned}\]Since if $x$ is a solution $\langle x \vert \phi _ 0\rangle = 0$, and $\langle x \vert \phi _ 1\rangle = \frac{1}{\sqrt S}$. Then
\[\begin{aligned} p(\text{measure a solution}) &= S \times \frac{\sin((2K+1)\theta)^2}{S} \\\\ &= \sin^2((2K+1)\theta) \end{aligned}\]To increase the probability, we then want to make $(2K+1)\theta$ as close to $\pi / 2$ as possible. Then since $\sin \theta := \sqrt{\frac S N}$ and $S \ll N$, $\theta \approx \sqrt{\frac S N}$. So choosing $K \approx \frac \pi 4 \sqrt{\frac N S} - \frac 1 2$ means $K \approx \frac{\pi}{4\theta} - \frac 1 2$. Then the difference between $\pi / 2$ and $(2K + 1)\theta$ is at most $\theta$, so
\[(2K + 1)\theta = \frac \pi 2 + \delta\]with $ \vert \delta \vert \le \theta$. Then
\[\begin{aligned} p(\text{measure a solution}) &= \sin^2((2K+1)\theta) \\\\ &= \sin^2\left(\frac \pi 2 + \delta\right) \\\\ &= \cos^2\delta \\\\ &\ge \cos^2 \theta \end{aligned}\]Since $\cos \theta := \sqrt{\frac{N-S}{N}\,}$, we have
\[p(\text{measure a solution}) \ge 1 - \frac S N\]as required.