Complex Analysis MT23, Complex integration
Flashcards
What does it mean for a function $F: [a, b] \to \mathbb C$ to be integrable, and can you define the integral?
$G, H$ are integrable where $F = G + iH$ and
\[\int^b_a F = \int^b_a G + i\int^b_a H\]What is true about the length and value of a line integral over the equivalence classes of oriented curves?
They are the same.
If $\gamma : [a, b] \to \mathbb C$ is a piecewise-$C^1$ path, can you define the integral of $f : \mathbb C \to \mathbb C$ along $\gamma$, i.e.
\[\int_\gamma f(z) \text d z\]
If $\gamma : [a, b] \to \mathbb C$ is a piecewise-$C^1$ path, can you define the integral of $f : \mathbb C \to \mathbb C$ along $\gamma$ with respect to arc-length, i.e.
\[\int_\gamma f(z) |\text d z|\]
Can you state and quickly prove the estimation lemma for complex integrals?
Suppose:
- $f : U \to \mathbb C$ continuous function on open subset $U \subseteq \mathbb C$
- $\gamma : [a, b] \to \mathbb C$ piecewise-$C^1$ path whose image lies in $U$
Then
\[\left|\int_\gamma f(z) \text d z\right| \le \sup_{z \in \gamma^\star} |f(z)| \ell(\gamma)\]Because (after convincing yourself that the supremum exists since $\gamma^\star$ compact)
\[\begin{aligned} \left| \int_\gamma f(z) \right| &= \left| \int^b_a f(\gamma(t))\gamma'(t) \text d t \right| \\\\ &\le \int^b_a |f(\gamma(t))| |\gamma'(t)|\text d t \\\\ &\le \sup_{z \in \gamma^\star} |f(z)| \int^b_a |\gamma'(t)| \text d t \\\\ &= \sup_{z \in \gamma^\star} |f(z)| \ell(\gamma) \end{aligned}\]What conditions do you need on a sequence of continuous functions $f _ n : U \to \mathbb C$ and a path $\gamma$ to be able to say
\[\int_\gamma f_n(z) \text d z \to \int_\gamma f(z) \text d z\]
Uniform convergence (suffices just on compact subsets of $U$).
Let $U \subseteq \mathbb C$ be an open set and let $f : U \to \mathbb C$ be a continuous function. What does it mean for $f$ to a have a primitive $F$ on $U$?
There exists a differentiable function $F : U \to \mathbb C$ with $F’(z) = f(z)$.
Can you state the fundamental theorem of calculus for complex integration?
Suppose:
- $U \subseteq \mathbb C$ open
- $f : U \to \mathbb C$ continuous
- $F : U \to \mathbb C$ primitive for $f$ ($F’ = f$)
- $\gamma : [a, b] \to U$ piecewise $C^1$ path in $U$
Then
\[\int_\gamma f(z) \text d z = F(\gamma(b)) - F(\gamma(a))\]The fundamental theorem of calculus for complex integration states, under suitable conditions, that
\[\int_\gamma f(z) \text d z = F(\gamma(b)) - F(\gamma(a))\]
What does this imply about the integral of any continuous function with a primitive around any closed path?
It is zero.
The fundamental theorem of calculus for complex integration states, under suitable conditions, that
\[\int_\gamma f(z) \text d z = F(\gamma(b)) - F(\gamma(a))\]
This implies that the integral of around any closed path of this function is equal to zero. Can you state a converse result, i.e. when can we say a continuous function will have a primitive?
Suppose
- $U$ is a domain
- $f : U \to \mathbb C$ continuous
- For any closed path $\gamma$ in $U$ we have $\int _ \gamma f(z) \text d z = 0$
Then $f$ has a primitive.
The fundamental theorem of calculus for complex integration states, under suitable conditions, that
\[\int_\gamma f(z) \text d z = F(\gamma(b)) - F(\gamma(a))\]
One of these conditions is that the integral of around any closed path of this function is equal to zero. We have the converse result that if
- $U$ is a domain
- $f : U \to \mathbb C$ continuous
- For any closed path $\gamma$ in $U$ we have $\int _ \gamma f(z) \text d z = 0$
Then $f$ has a primitive. How do we define a function $F$ that we show is a primitive when proving this?
where $\gamma(a) = z _ 0$, $\gamma(b) = z$ for some $z _ 0$ in $U$.
How can you show that a continuous function $f : U \to \mathbb C$ doesn’t have a primitive?
Show that
\[\int_\gamma f(z) \text d z \ne 0\]for some closed path $\gamma$.
What does it mean for a domain $D \subseteq C$ is primitive?
Any holomorphic function $f : D \to \mathbb C$ has a primitive in $D$.
Suppose that
- $D _ 1$ and $D _ 2$ are primitive domains
- $D _ 1 \cap D _ 2$ is connected
Then what can you deduce?
is primitive.
What’s the technique for tackling integrals of the form
\[\int^{2\pi}_0 \frac{p(\cos \theta, \sin\theta)}{q(\cos\theta, \sin\theta)} \text d\theta\]
Where $p$ and $q$ are polynomials in $\cos$ and $\sin$?
Rewriting using $e^{i\theta}$, then making the substitution $e^{i\theta} \mapsto z$ and integrating on the unit circle.
Suppose you are working out an integral and you get to a stage like
\[\int^{2\pi}_0 \frac{1}{1 - \frac a 2 e^{i\theta} - \frac a 2 e^{-i\theta}\\,} \text d \theta\]
What subsitution do you make, and what does $\text d \theta$ become?
and
\[\text d \theta = \frac{1}{iz} \text d z\]The fundamental theorem of calculus for complex integration states, under suitable conditions, that
\[\int_\gamma f(z) \text d z = F(\gamma(b)) - F(\gamma(a))\]
One of these conditions is that the integral of around any closed path of this function is equal to zero. Quickly prove the converse result, that if
- $U$ is a domain
- $f : U \to \mathbb C$ continuous
- For any closed path $\gamma$ in $U$ we have $\int _ \gamma f(z) \text d z = 0$
Then $f$ has a primitive.
Pick an arbitrary point $a \in U$ and define
\[F(z) = \int_{\gamma_{z}\\,} f(w) \text dw\]where
\[\gamma_z : [0, 1] \to U\]is any path where $\gamma _ z(0) = a$ and $\gamma _ z(1) = z$. We aim to show that this $F$ is a primitive.
Note that this is well defined since the definition does not depend on the choice of specific path $\gamma _ z$. Suppose $\gamma _ z$ and $\gamma _ z’$ are two such paths, then $\gamma _ z \star (\gamma _ {z}’)^{-}$ is a closed path, so by assumption
\[0 = \int_{\gamma_z \star (\gamma_{z}')^{-}\\,} f(w) \text dw = \int_{\gamma_z} f(w) \text dw - \int_{\gamma_{z}'} f(w) \text dw\]so
\[\int_{\gamma_z} f(w) \text dw = \int_{\gamma_{z}'} f(w) \text dw\]Then we claim $F$ is differentiable with $F’(z) = f(z)$. Fix an arbitrary point $z _ 0 \in U$ for which we want to show $F$ is differentiable at, and take $\varepsilon > 0$ such that
\[B(z_0, \varepsilon) \subseteq U\]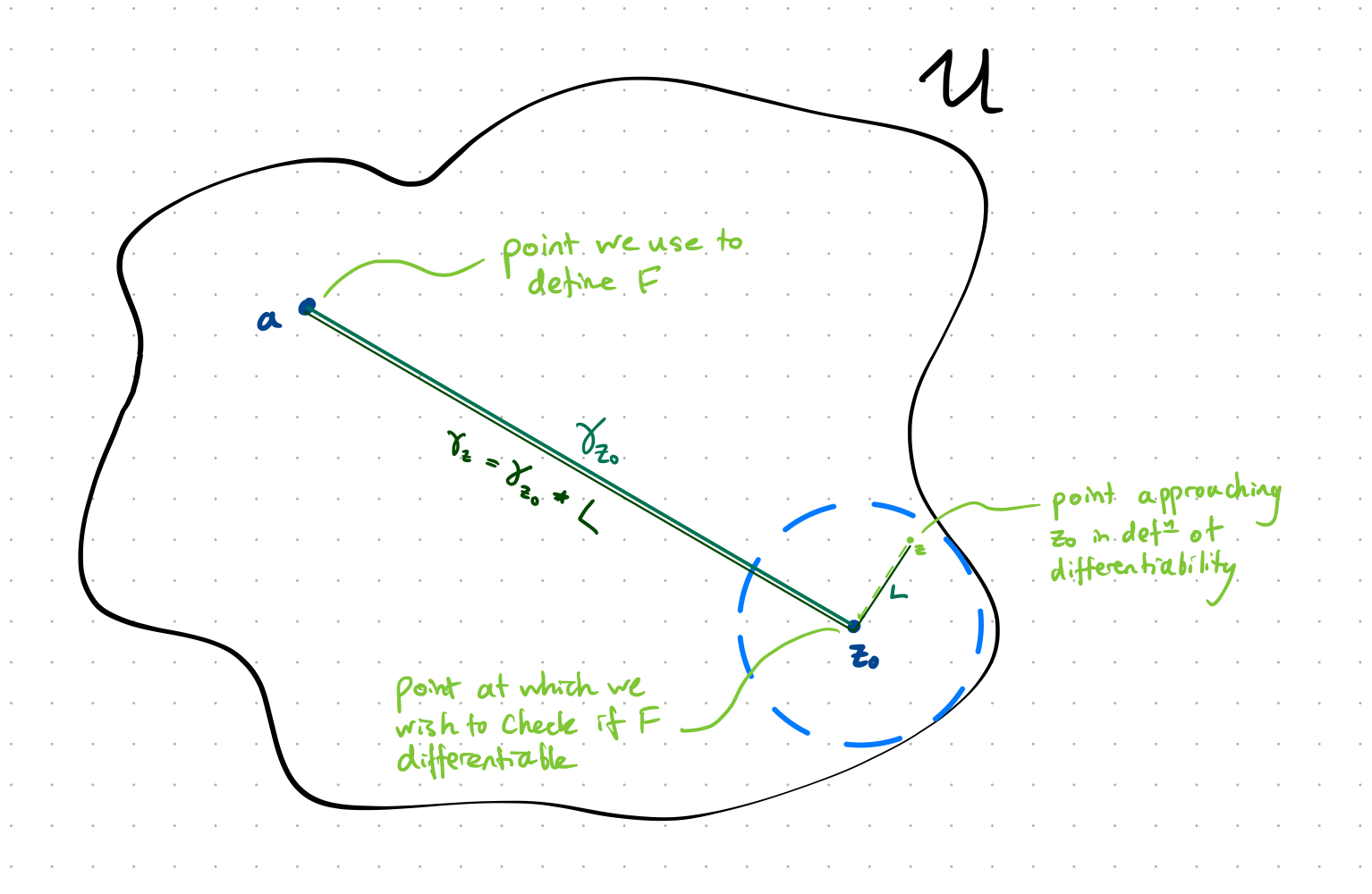
The idea is to show that
\[\left| \frac{F(z_0) - F(z)}{z_0 - z} - f(z_0)\right|\]can be made arbitrarily close to $0$ as $z _ 0 \to z$ where $z _ 0 \in B(z, \varepsilon)$. Note that
\[\begin{aligned} F(z_0) - F(z) &= \int_{\gamma_{z_0}\\,} f(w) \text dw - \int_{\gamma_z} f(w) \text dw \end{aligned}\]by taking $\gamma _ {z}$ to be the concatenation of $\gamma _ {z _ 0}$ and $L$, the straight line path from $z _ 0$ to $z$ given by $t \mapsto z _ 0 + t(z - z _ 0)$, we have
\[\begin{aligned} F(z_0) - F(z) &= \int_{\gamma_{z_0}\\,} f(w) \text dw - \int_{\gamma_{z_0}\\,} f(w) \text dw - \int_L f(w) \text dw \\\\ &= -\int_L f(w) \text dw \end{aligned}\]Thus
\[\begin{aligned} \left| \frac{F(z_0) - F(z)}{z_0 - z} - f(z_0)\right| &= \left| \frac{F(z) - F(z_0)}{z - z_0} - f(z_0)\right| \\\\ &=\left|\frac{1}{z-z_0} \left( \int_L f(w) \text dw \right) - f(z_0)\right| \\\\ &= \left|\int^1_0 f(z_0 + t(z - z_0)) \text dt - f(z_0)\right| \\\\ &= \left|\int^1_0 f(z_0 + t(z - z_0)) - f(z_0) \text dt \right| \\\\ &\le \sup_{t \in [0, 1]} | f(z_0 + t(z - z_0)) - f(z_0) | \\\\ &\to 0 \text{ as } z \to z_0\end{aligned}\](where we ignore the minus sign, and the last line follows from the continuity of $f$). Then $F$ is differentiable at $z _ 0$, with derivative $f(z _ 0)$.
Suppose:
- $f _ n : U \to \mathbb C$ is a sequence of continuous functions
- $f _ n \stackrel{u}{\to} f$
- $\gamma : [0, 1] \to U$ is a contour
What’s a sufficient condition on $\gamma$ to conclude that
\[\int_\gamma f_n \to \int_\gamma f\]
?
$\gamma^\star$ is sequentially compact.
(This is used in the proof of the fact that if $f _ n$ are holomorphic, then so is $f$).
Proofs
Quickly prove that if $\gamma : [a, b] \to \mathbb C$ and $\tilde \gamma : [c, d] \to \mathbb C$ are equivalent (piecewise) $C^1$ paths on the complex plane, then for continuous $f$
\[\int_\gamma f(z) \text d z = \int_\tilde{\gamma} f(z) \text d z\]
and
\[\int_\gamma f(z) |\text d z| = \int_\tilde{\gamma} f(z) |\text d z|\]
Since $\tilde \gamma$ is equivalent to $\gamma$, there exists a continuously differentiable function $s : [c, d] \to [a, b]$ with $s(c) = a, s(d) = b$ and $s’(t) > 0$ for all $t \in [c, d]$. For the case where $\gamma$ is $C^1$ (rather than piecewise $C^1$):
\[\begin{aligned} \int_{\tilde \gamma} f(z) \text dz &= \int^d_c f(\gamma(s(t)))(\gamma \circ s)'(t) \text dt \\\\ &= \int^d_c f(\gamma(s(t))) \gamma'(s(t))s'(t) \text dt \\\\ &= \int^b_c f(\gamma(s)) \gamma'(s) \text dt && \text{(change of vars)} \\\\ &= \int_\gamma f(z) \text dz \end{aligned}\]The piecewise $C^1$ case is an easy generalisation (just split up over a sum), and the integral with respect to arc length is the same but you use $ \vert \gamma’(t) \vert $.
Suppose that $D _ 1$ and $D _ 2$ are primitive domains and $D _ 1 \cap D _ 2$ is connected. Quickly justify why $D _ 1 \cup D _ 2$ is also primitive.
Consider the primitives that must exist on either domain, and then use the fact that $F _ 1 - F _ 2$ must be constant on $D _ 1 \cap D _ 2$.