Notes - Complex Analysis MT23, Cauchy's integral formula

Suppose

• $U$ open set
• $f : U \to \mathbb C$ holomorphic
• $U \supseteq \bar B(a, r)$

Then for all $w \in B(a, r)$, we have

\[f(w) = \frac{1}{2\pi i} \int_\gamma \frac{f(z)}{z-w} \text dz\]

where

\[\gamma(t) = a + re^{2\pi i t}\]

Draw a picture: consider contours $\Gamma _ 1$ and $\Gamma _ 2$ where we have a disc about $a$, with some point $w$ on the inside, and $\Gamma _ 1$ loops around a small $\varepsilon$-bump on the outside of $w$ and half of the circle, and $\Gamma _ 2$ loops around the other side.

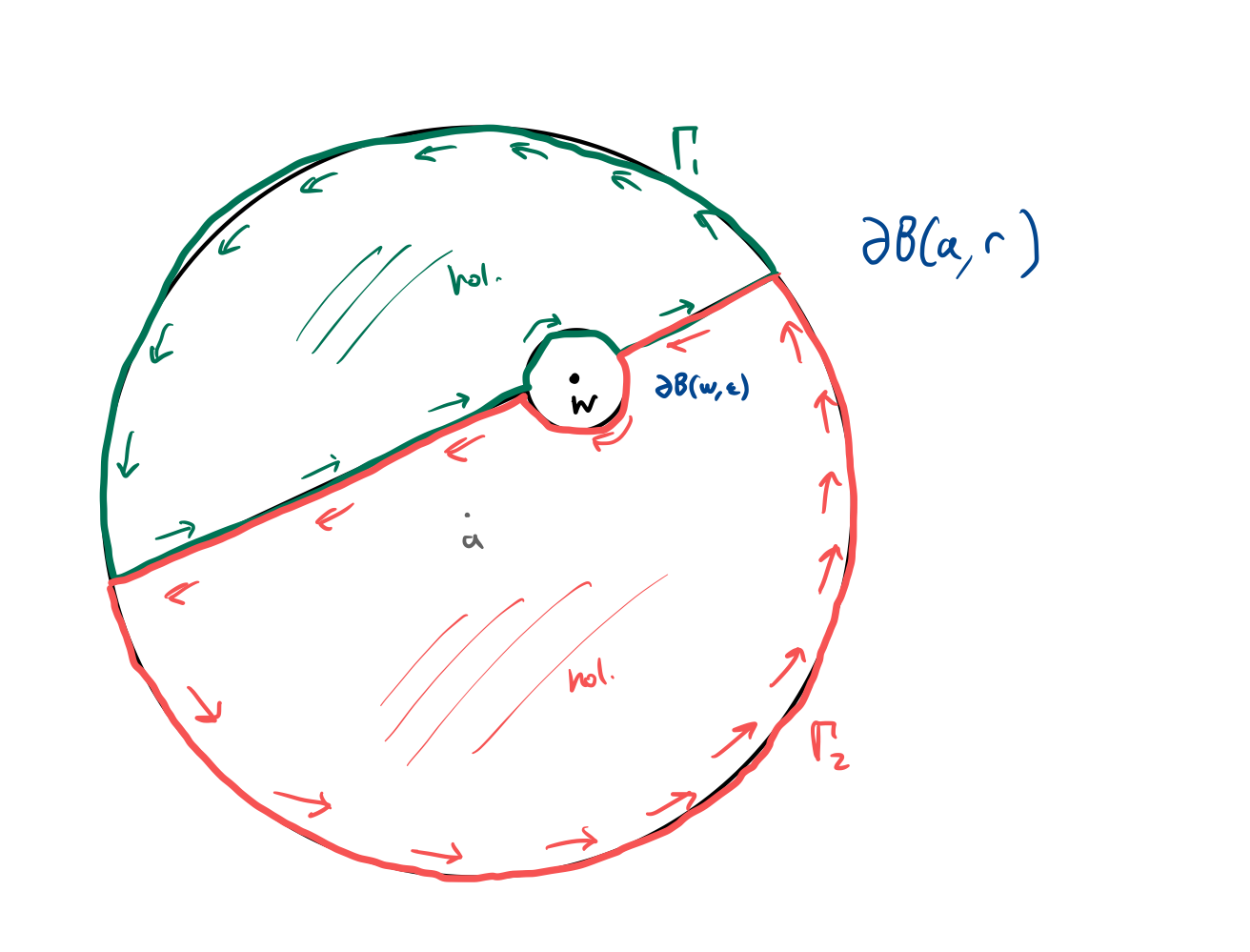
Then, by additivity properties of the path integrals,

\[\int_{\Gamma_1} \frac{f(z)}{z - w} \text d z + \int_{\Gamma_2} \frac{f(z)}{z - w} \text dz = \int_{\gamma(a, r)} \frac{f(z)}{z - w} \text d z - \int_{\gamma(w, \varepsilon)} \frac{f(z)}{z-w} \text dz\]

But by Cauchy’s theorem the integrals on the LHS are $0$, so we have

\[\begin{aligned} \int_{\gamma(a, r)} \frac{f(z)}{z - w} \text d z &= \int_{\gamma(w, \varepsilon)} \frac{f(z)}{z-w} \text dz \\\\ &= \int_{\gamma(w, \varepsilon)} \frac{f(z) - f(w)}{z - w} \text d z + f(w)\int_{\gamma(w, \varepsilon)} \frac{1}{z-w} \text d z \\\\ &= \int_{\gamma(w, \varepsilon)} \frac{f(z) - f(w)}{z - w} \text d z + f(w) \times 2\pi i I(\gamma, w) \end{aligned}\]

but then, since $f$ is holomorphic at $z = w$, remaining integral on the RHS must tend towards $0$ as $\varepsilon \to 0$, hence it follows:

\[f(w) = \frac{1}{2\pi i}\int_{\gamma(a, r)} \frac{f(z)}{z -w} \text d z\]

For every compact subset $K$ of $U$, the sequence $(f _ n \vert _ K)$ converges uniformly to $f _ K$.

$f _ n \to f$ only has to converge uniformly on compact subsets of $U$.

Suppose

• $f : U \to \mathbb C$ holomorphic
• $\gamma$ closed path in $U$ (i.e. $I(\gamma, z) = 0$ for all $z \notin U$)

Then, for all $z \in U \setminus \gamma^\star$:

\[\int_\gamma f(w) \text dw = 0\]

(a form of Cauchy’s theorem), and

\[\int_\gamma \frac{f(w)}{w - z} \text d w = 2\pi i I(\gamma, z)f(z)\]

Better since it works for any domain where $\gamma$ lies in domain.

\[\begin{aligned} f(w) &= \frac{1}{2\pi i} \int_{\partial B} \frac{f(z)}{z-w} \text d z \\\\ &= \frac{1}{2\pi i} \int_{\partial B} \frac{f(z)}{z\left(1-\frac w z\right)} \text d z\\\\ &= \frac{1}{2\pi i} \int_{\partial B} \sum^\infty_{k = 0} \frac 1 z f(z) \cdot \left(\frac w z \right)^k \text d z \\\\ &= \frac{1}{2\pi i} \sum^\infty_{k = 0} w^k \cdot \frac{1}{2\pi i}\int_{\partial B} \frac{f(z)}{z^{k+1}\\,} \text d z \\\\ \end{aligned}\]

$f$ is continuous: Pick some $a \in U$, then since $U$ is open, $\exists r > 0$ s.t. $B(a, r) \subseteq U$. But then $K = \overline B(a, r/2) \subseteq U$, and $f _ n \to f$ uniformly on $K$, so $f$ is continuous on $K$, and so continuous at $a$.

$f$ is holomorphic: Pick some $w \in U$ and again find $r > 0$ such that $B(w, r) \subseteq U$. Then $B(w, r)$ is convex, so Cauchy’s theorem shows that for every closed path $\gamma: [a, b] \to B(w, r)$ we have

\[\int_\gamma f_n(z) \text dz = 0 \quad \forall n \in \mathbb N\]

But $\gamma^\star = \gamma([a, b])$ is a compact subset of $U$. Hence $f _ n \to f$ uniformly on $\gamma^\star$. It then follows

\[0 = \int_\gamma f_n(z) \text dz \to \int_\gamma f(z) \text dz\]

So the integral of any closed path in $B(w, r)$ is zero. Then by Morera’s theorem, $f$ is holomorphic on $B(w, r)$.

Fix some $z _ 0 \in B(0, r)$. Then since $ \vert z _ 0 \vert < r$, $ \vert z - z _ 0 \vert > 1 - r$, and so by the estimation lemma and Cauchy’s integral formula:

\[\begin{aligned} |f_n^{(k)}(z_0) - f^{(k)}(z_0)| &= \left| \frac{1}{2\pi i} \int_\gamma \frac{f_n(z) - f(z)}{(z- z_0)^{k+1}} \text dz \right| \\\\ &\le \sup_{|z| = 1} \frac{|f_n(z) - f(z)|}{(1 - r)^{k+1}} \end{aligned}\]

This shows that $f _ n^{(k)} \to f^{(k)}$, not necessarily uniformly. Then note that

\[\sup_{|z_0| < r} |f^{(k)}_n(z_0) - f^{(k)}(z_0)| \le \sup_{|z| = 1} \frac{|f_n(z) - f(z)|}{(1 - r)^{k+1}}\]

since we removed the dependence on $z _ 0$ in the integral. So $f _ n^{(k)}$ converges uniformly to $f^{(k)}$ on $B(0, r)$.

Let $\gamma$ be the contour around the unit circle. Then

\[\int_\gamma p_n(z) \text dz = 0\]

for each $n$, but supposedly

\[\int_{\gamma} \frac 1 z \text dz = 2\pi i\]

a contradiction, since by uniform convergence, these integrals would be equal.

Todo, consider $1/p$, and use the fact that if it were bounded then Lioville’s theorem would imply that it was constant.