Models of Computation MT23, DFAs
Flashcards
Can you give the formal definition of a DFA?
A 5-tuple $(Q, \Sigma, \delta, q _ 0, F)$ where
- $Q$ is a finite set of states
- $\Sigma$ is a finite set called the “alphabet”
- $\delta : Q \times \Sigma \to Q$ is the transition function
- $q _ 0 \in Q$ is the start state
- $F \subseteq Q$ is the set of accepting states
If $w = a _ 1 a _ 2 \cdots a _ n \in \Sigma^\star$, what does it mean for $q \xrightarrow[]{w}^\star q’$?
There exist transitions
\[q \xrightarrow[]{a_1} q_1 \xrightarrow[]{a_2} \cdots \xrightarrow[]{a_n} q_n = q'\]How can you define $L(M)$, the language recognised by some DFA $M$?
The set of strings $w$ over $\Sigma$ such that $q _ 0 \xrightarrow[]{w}^\star q$ where $q$ is an accepting state.
Suppose we have $M _ 1$ and $M _ 2$ recognising $A$ and $B$ respectively where
\[\begin{aligned}
M_1 &= (Q_1, \Sigma, \delta_1, q_1, F_1) \\\\
M_2 &= (Q_2, \Sigma, \delta_2, q_2, F_2)
\end{aligned}\]
Then how can you define a DFA that recognises both languages?
Let $M = (Q, \Sigma, \delta, q _ 0, F)$ where
\[\begin{aligned} Q &= Q_1 \times Q_2 \\\\ \delta((r_1, r_2), a) &= (\delta_1(r_1, a), \delta_2(r_2, a)) \\\\ q_0 &= (q_1, q_2) \\\\ F &= (F_1 \times Q_2) \times (Q_1 \times F_2) \end{aligned}\]Suppose $M$ is a DFA. How can you determine whether $ \vert L(M) \vert = k$?
- See if any accepting state is contained in a directed cycle reachable from the start state. If it is, then $ \vert L(M) \vert $ is infinite, so output “no”.
- Otherwise, let $t$ be the size of the DFA. Iterate over all words of length $t$. If exactly $k$ of them accept, output “yes”. Otherwise output “no”.
(this might be exponential time in the worst case I think, so this is not an efficient algorithm)
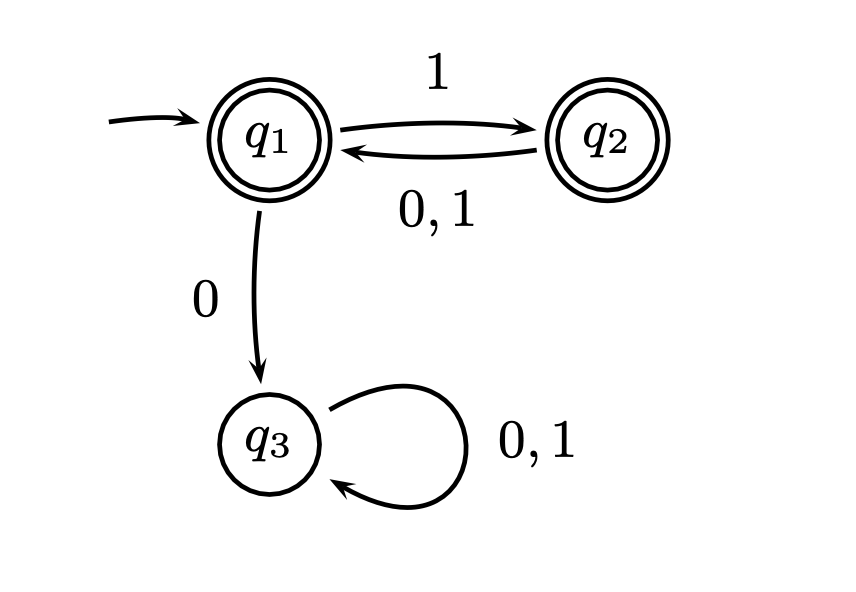
Draw a DFA that accepts
\[L = \\{w \in \\{0, 1\\}^\star \mid \text{every odd position of }w \text{ is } 1\\}\]
Quickly prove that if $A$ and $B$ are regular languages, then $A \cup B$ is also regular.
Use the product construction. Suppose we have $M _ 1$ and $M _ 2$ recognising $A$ and $B$ respectively where
\[\begin{aligned} M_1 &= (Q_1, \Sigma, \delta_1, q_1, F_1) \\ M_2 &= (Q_2, \Sigma, \delta_2, q_2, F_2) \end{aligned}\]then let $M = (Q, \Sigma, \delta, q _ 0, F)$ where
\[\begin{aligned} Q &= Q_1 \times Q_2 \\ \delta((r_1, r_2), a) &= (\delta_1(r_1, a), \delta_2(r_2, a)) \\ q_0 &= (q_1, q_2) \\ F &= (F_1 \times Q_2) \cup (Q_1 \times F_2) \end{aligned}\](this is slightly informal, since you would then need to prove that $L(M) = L(M _ 1)\cup L(M _ 2)$).