Notes - Logic and Proof MT24, Presburger arithmetic

The theory of the structure $(\mathbb N, 0, 1, +, <)$ under the intended interpretation (@todo, is this an accurate definition? Or should you state the axioms?)

\[\text{Th}(\mathbb N, 0, 1, +, <)\]

is decidable.

It suffices to show that $\text{Th}(\mathbb N, 0, 1, +)$ is decidable, since any formula over $(\mathbb N, 0, 1, +, <)$ can be rewritten as a formula using $+$ and $=$ that defines the same property on $\mathbb N$ (@todo, actually check this).

To show this is decidable, we reduce determining whether a statement is satisfiable to membership of a specific word in a regular languages.

Consider a quantifier-free formula $F$ over variables $x _ 1, \ldots, x _ n$ and consider the corresponding alphabet

\[\Sigma_n = \\{ \begin{bmatrix} 0 \\\\ 0 \\\\ \vdots \\\\ 0 \end{bmatrix}, \dots, \begin{bmatrix} 1 \\\\ 1 \\\\ \vdots \\\\ 1 \end{bmatrix} \\}\]

which represents a valuation of these variables using little endian, where the value of $x _ i$ corresponds to the $i$-th row of the vector.

Define $A _ =$ representing the subset of $\Sigma _ 2^\ast$ where the elements satisfy $x _ 1 = x _ 2$ by the DFA:

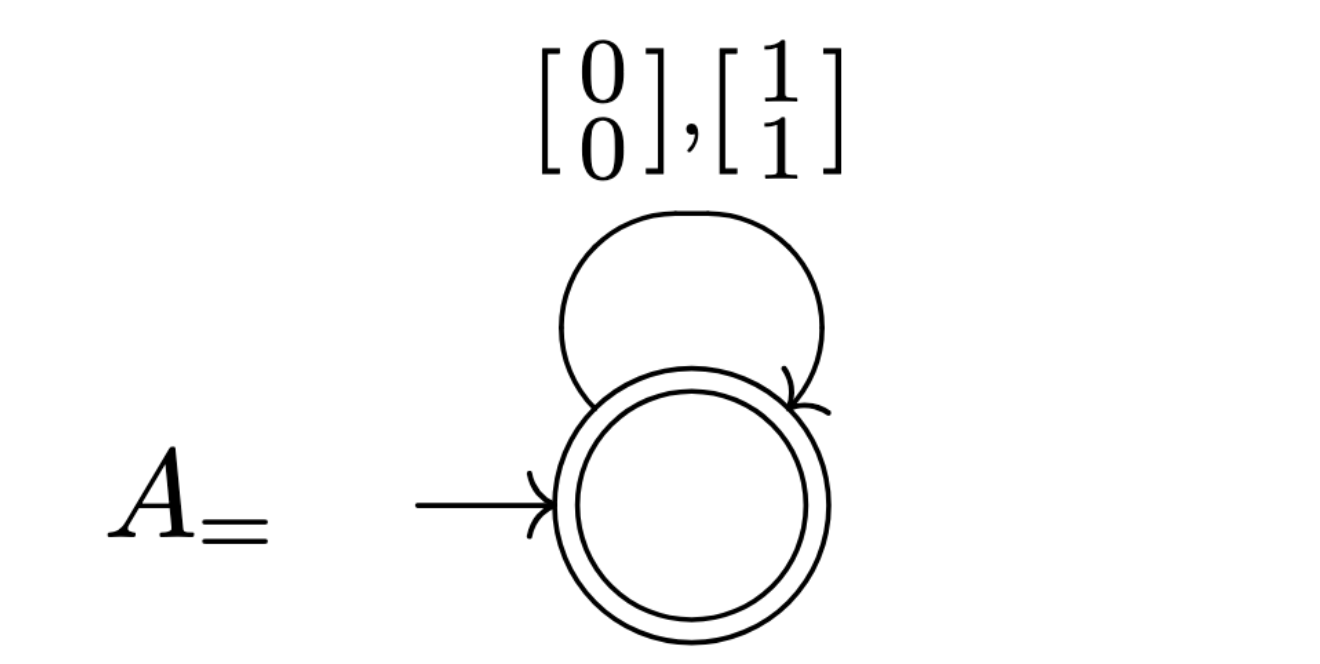
And define $A _ +$ representing the subset of $\Sigma _ 3^\ast$ where the elements satisfy $x _ 1 + x _ 2 = x _ 3$ by:

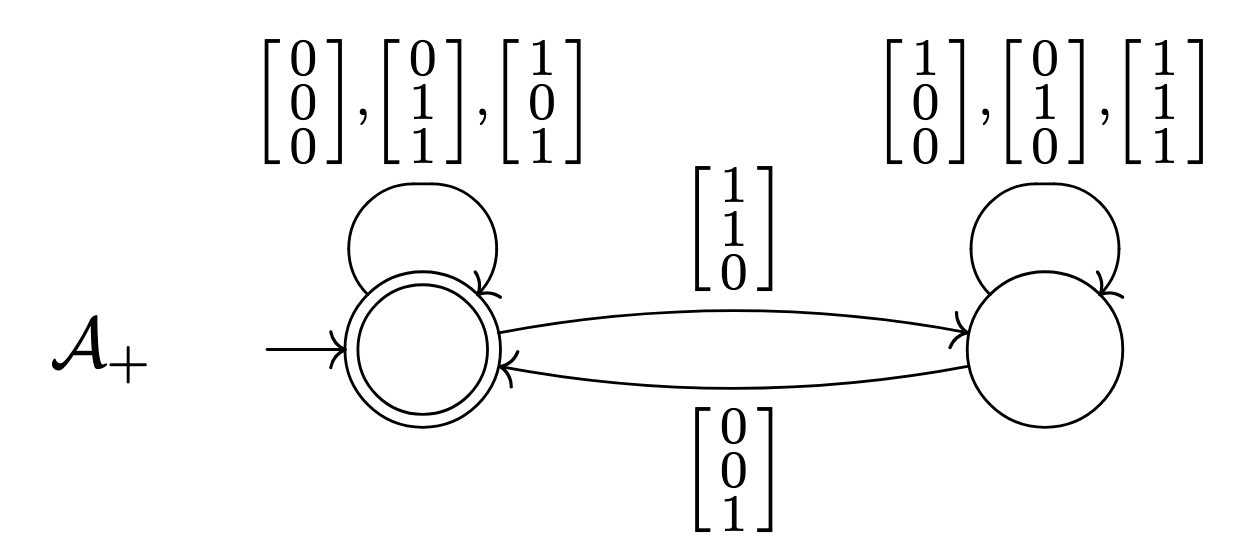
We now define $A _ F$ by induction on the structure of $F$. Define

\[\pi_{} : \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \mapsto \begin{bmatrix} x_i \\ \vdots \\ x_k \end{bmatrix}\]

• Base case: $x _ i = x _ j$, take $A _ F$ to be the DFA for the language defined by $\pi _ {i, j}^{-1}(L(A _ =))$, which is valid as regular languages are closed under inverse homomorphisms.
• Base case: $x _ i + x _ j = x _ k$, take $A _ F$ to be the DFA for the language defined by $\pi _ {i,j,k}^{-1}(L(A _ +))$.
• Case: $F = F _ 1 \wedge F _ 2$. Take $A _ F$ to be an automaton whose language is $L(A _ {F _ 1}) \cap L(A _ {F _ 2})$.
• Case: $F = \lnot G$. Take $A _ F$ to be an automaton whose language is $\Sigma^\ast _ n \setminus L(A _ G)$.

This covers all quantifier-free formulas.

Now consider a sentence

\[Q_1 x_1 \cdots Q_n x_n F\]

in prenex form. For $k = 0, \ldots, n$ we write $F _ k := Q _ {k+1} x _ {k+1} Q _ n x _ n F^\ast$ an define a corresponding automaton $A _ k$ over alphabet $\Sigma _ k$ such that $A _ k$ accepts the set of values of variables $x _ 1, \ldots, x _ k$ that satisfy $F _ k$. An invariant is that $A _ k$ has non-empty lanugage iff formula $F _ k$ is satisfiable.

Take $A _ n$ to be $A _ F$.

Now suppose that $F _ {k-1} = \exists x _ k F _ k$. By induction, $A _ k$ is an automaton on an alphabet $A _ k$ corresponding to $F _ k$. Define $A _ {k-1}$ to be an automaton whose lanugage is $\pi(L(A _ k))$ where $\pi : \Sigma _ k \to \Sigma _ {k-1}$ is the map that projects out the $k$-th coordinate of each tuple in $\Sigma _ k$.

Handle the universal quantifier $\forall x _ k$ by treating it as shorthand for $\lnot \exists x _ k \lnot$.

We end up with an automaton $A _ 0$ for the sentence $F _ 0$ over the alphabet $\Sigma _ 0$. This automaton has non-empty lanugage iff $(\mathbb N, +, 0, 1)$ satisfies $F _ 0$.