Lecture - Theories of Deep Learning MT25, IV, Data classes for which DNNs can overcome the curse of dimensionality
Visualise the figure in Hein (2020) describing the “hidden manifold model”.

@Define the hidden manifold model as in Hein (2020) for generating datasets.
where
- $F \in \mathbb R^{d, n}$ are the $d$ features used to represent the data
- $C \in \mathbb R^{p, d}$ combines the $d < n < p$ features
- $f$ is a nonlinear function
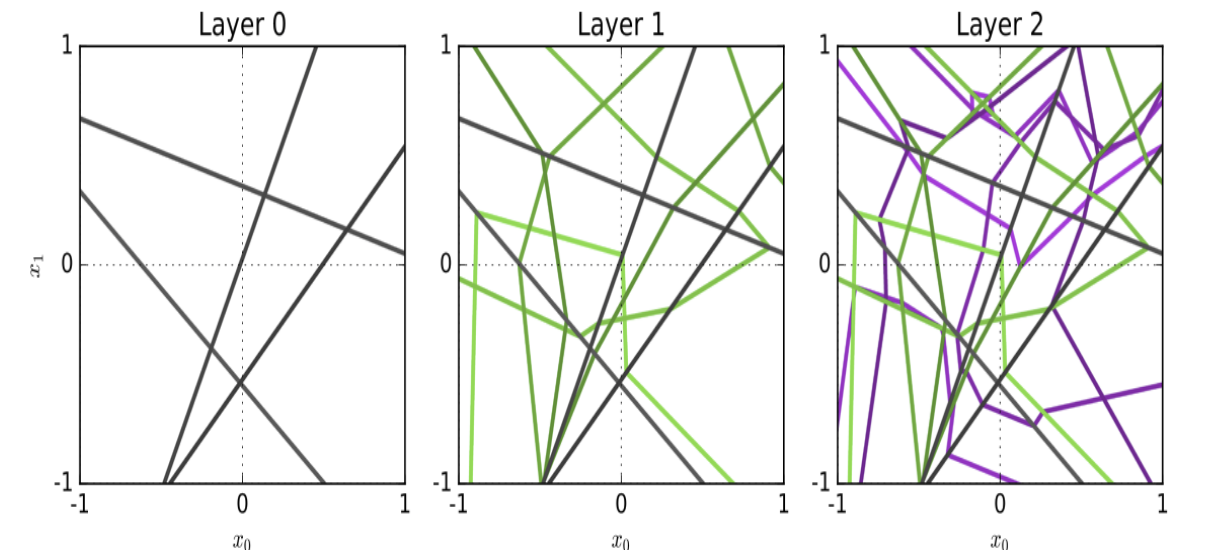
How does Pascanu (2014) make an argument for the expressivity of ReLU DNNs based on hyperplane arrangements?
Since ReLU is piecewise linear, the output of a ReLU DNN is a piecewise linear function. They show that the number of possible regions of the input where the function can take on a different linear function is at least
\[\prod^L _ {\ell = 0} n _ \ell^{\text{min}\{n _ 0, n _ \ell / 2\}}\]where the input is $\mathbb R^{n _ 0}$ and the hidden layers are of width $n _ 1, \ldots, n _ L$.
How does Raghu (2016) make an argument for the expressivity of DNNs based on trajectory lengths?
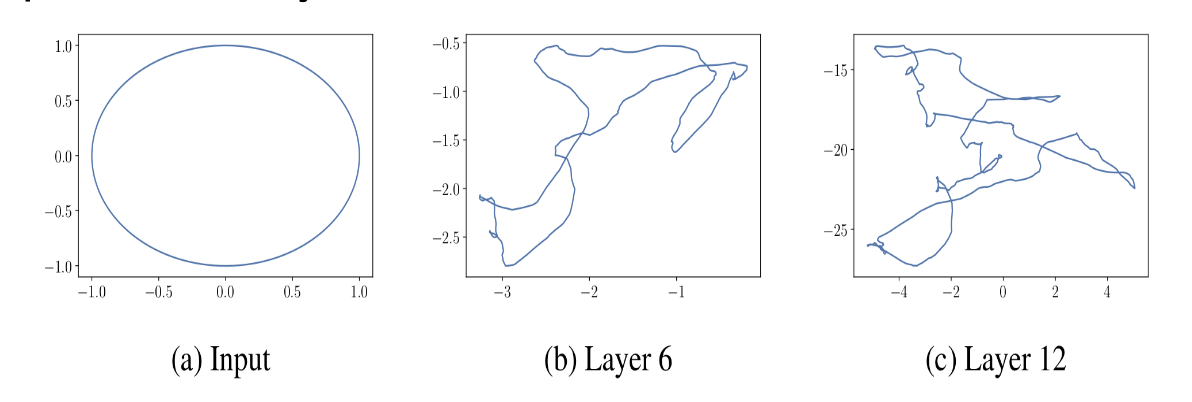
They show that a circle passed through a random DNN with an increasing number of layers can draw more and more complicated shapes, formalised as a growing arc length in expectation.
Papers mentioned
- [[Paper - Error bounds for approximations with deep ReLU networks, Yarotsky]]U
- [[Paper - When and when can deep networks avoid the curse of dimensionality, Poggio (2016)]]U Why and When Can Deep – but Not Shallow – Networks Avoid the Curse of Dimensionality: a Review
- Intrinsic Dimensionality Estimation of Submanifolds in $\mathbb R^d$
- Modeling the Influence of Data Structure on Learning in Neural Networks: The Hidden Manifold Model
- Deep Neural Network Approximation Theory
- On the number of response regions of deep feedforward networks with piecewise linear activations
- On the Expressive Power of Deep Neural Networks
- Trajectory growth lower bounds for random sparse deep ReLU networks
- Survey of Expressivity in Deep Neural Networks