Paper - Representation Benefits of Deep Feedforward Networks, Telgarsky (2015)

Created: October 18, 2025 | Updated: October 19, 2025 | About these notes | View in context | Study these flashcards

Summary

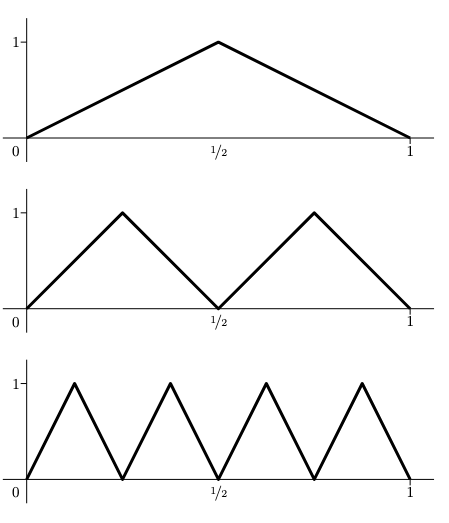
This note provides a family of classification problems, indexed by a positive integer $k$, where all shallow networks with fewer than exponentially (in $k$) many nodes exhibit error at least $1/6$, whereas a deep network with $2$ nodes in each of the $2k$ layers achieves zero error, as does a recurrent network with $3$ distinct nodes iterated $k$ times. The proof is elementary, and the networks are standard feedforward networks with ReLU nonlinearities.

This demonstrates why the “deep” part of “deep learning” is important; depth in a network allows it to be as expressive as a shallow network with exponentially many nodes.

Flashcards

Let:

  • $\mathfrak R(\sigma; m, l)$ denote the set of possible functions of a neural networks with $l$ layers and $m$ nodes.
  • $\tilde f(x) = \mathbb 1[f(x) \ge 1/2]$ denote the classifier corresponding to a function $f : \mathbb R^d \to \mathbb R$
  • $\mathcal R _ z(f) := n^{-1} \sum _ i \mathbb 1[\tilde f(x _ i) \ne y _ i]$ for a set of points $((x _ i, y _ i))^n _ {i = 1}$ with $x _ i \in \mathbb R^d$ and $y _ i \in {0, 1}$.

@State the theorem in Telgarsky (2015) which formalises the importance of depth in a neural networks.

Suppose:

  • $k$ is a positive integer
  • $l$ is the number of layers
  • $m$ is the number of nodes per layer
  • $m \le 2^{(k-3)/l-1}$

Then there exists a collection of $2^k$ points $((x _ i, y _ i))^n _ {i = 1}$ with $x _ i \in [0, 1]$ and $y \in {0, 1}$ such that

\[\min _ {f \in \mathfrak{R}(\sigma _ R; 2, 2k} \mathcal R _ z(f) = 0\]

and

\[\min _ {g \in \mathfrak{R}(\sigma _ R; m, l)} \mathcal R _ z(g) \ge \frac 1 6\]

Let:

  • $\mathfrak R(\sigma; m, l)$ denote the set of possible functions of a neural networks with $l$ layers and $m$ nodes.
  • $\tilde f(x) = \mathbb 1[f(x) \ge 1/2]$ denote the classifier corresponding to a function $f : \mathbb R^d \to \mathbb R$
  • $\mathcal R _ z(f) := n^{-1} \sum _ i \mathbb 1[\tilde f(x _ i) \ne y _ i]$ for a set of points $((x _ i, y _ i))^n _ {i = 1}$ with $x _ i \in \mathbb R^d$ and $y _ i \in {0, 1}$.

Telgarsky (2015) proves that if

  • $k$ is a positive integer
  • $l$ is the number of layers
  • $m$ is the number of nodes per layer
  • $m \le 2^{(k-3)/l-1}$

Then there exists a collection of $2^k$ points $((x _ i, y _ i))^n _ {i = 1}$ with $x _ i \in [0, 1]$ and $y \in {0, 1}$ such that

\[\min _ {f \in \mathfrak{R}(\sigma _ R; 2, 2k)} \mathcal R _ z(f) = 0\]

and

\[\min _ {g \in \mathfrak{R}(\sigma _ R; m, l)} \mathcal R _ z(g) \ge \frac 1 6\]

What’s the rough idea behind the proof?

Consider “$n$-ap” (alternating points) classification problems like the following:

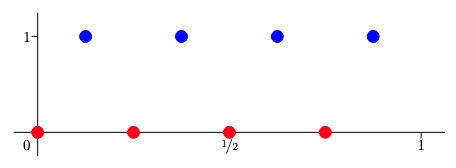
  • For the lower bound, show that a shallow network has to be a sawtooth-like function, and that sawtooth functions can only cross the origin a few amount of time.
  • For the upper bound, show how composing a “mirror map” with itself lets you create sawtooth functions with exponentially many spikes.



Related posts