Paper - When and when can deep networks avoid the curse of dimensionality, Poggio (2016)
- Full title: Why and When Can Deep – but Not Shallow – Networks Avoid the Curse of Dimensionality: a Review
- Author(s): Tomaso Poggio, Hrushikesh Mhaskar, Lorenzo Rosasco, Brando Miranda, Qianli Liao
- Year: 2016
- Link: https://arxiv.org/pdf/1611.00740
- Relevant for:
- Links to:
Summary
The paper characterises classes of functions for which deep learning can be exponentially better than shallow learning. Deep convolutional networks are a special case of these conditions, though weight sharing is not the main reason for their exponential advantage.
There are three main sets of theory questions about Deep Neural networks.
- The first set of questions is about the power of the architecture: which classes of functions can it approximate and learn well?
- The second set of questions is about the learning process: why is SGD so unreasonably efficient, at least in appearance?
- Generalisation: Overparameterisation may explain why minima are easy to find during training but then why does overfitting seem to be less of a problem than for classical shallow networks? Is this because deep entworks are very efficient algorithms for hierarchical vector quantisation?
in this paper we focus especially on the first set of questions, summarising several theorems that have appeared online in 2015 and in 2016.
…
The main message is that deep networks have the theoretical guarantee, which shallow networks do not have, that they can avoid the curse of dimensionality for an important class of problems, corresponding to compositional functions, that is functions of functions.
Flashcards
Telgarsky (2015) makes the observation that deep networks can be exponentially more compact than shallow networks at approximating a particular function formed from iterating a sawtooth. How does Poggio (2017) generalise this?
They consider other classes of “compositional” functions for deep networks can dramatically outperform shallow networks.
Telgarsky (2015) makes the observation that deep networks can be exponentially more compact than shallow networks at approximating a particular function formed from iterating a sawtooth. Poggio (2017) generalises this by considering other classes of “compositional” functions for deep networks can dramatically outperform shallow networks.
What’s one particular class of functions they consider, and what do they observe?
They define $W _ m^{n, 2}$ as the set of all compositional functions $f$ of $n$ variables and constituent functions of $n$ variables with binary tree structure with $m$ bounded derivatives.
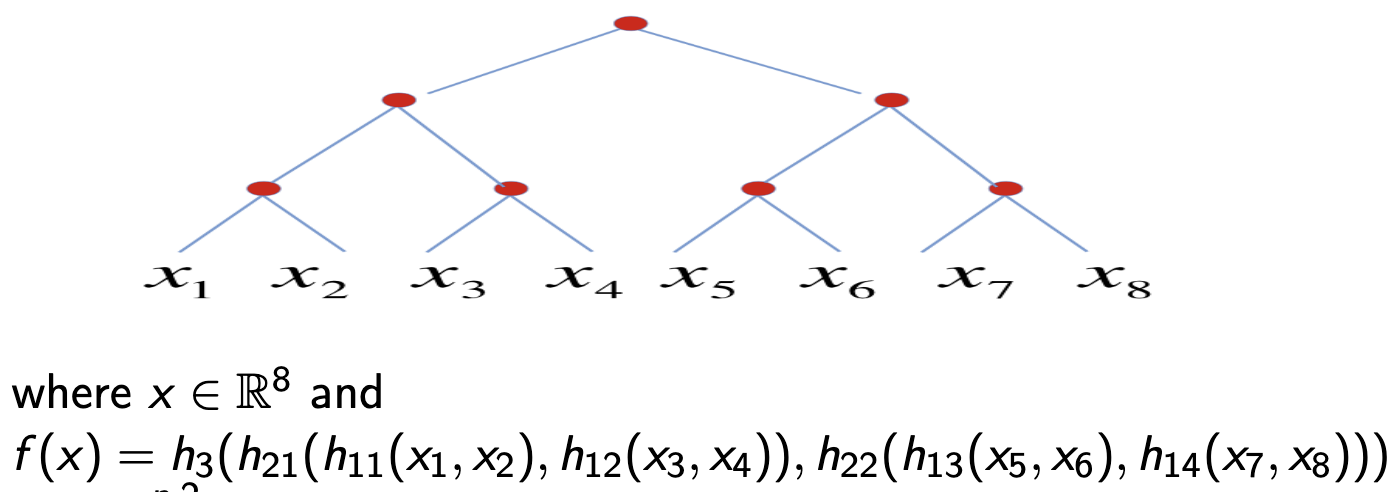
Then if $f \in W^{n, n} _ m$, taking a DNN with the same tree structure and an infinitely differentiable activation function $\sigma$, then $f$ can be approximated to an error of $\epsilon$ with $O((n-1)\epsilon^{-2/m})$ weights.
How does Poggio (2016) @define the effective dimensionality of a function class $W$?
The effective dimensionality of a function class $W$ is said to be $d$ if for every $\epsilon > 0$, any function within $W$ can be approximated within an accuracy $\epsilon$ by a DNN at rate $\epsilon^{-d}$.