Lecture - Uncertainty in Deep Learning MT25, Bayesian probabilistic modelling
Measuring the temperature
Suppose you measure the temperature this morning and your phone tells you that the temperature is 8°C, but the manufacturer’s specification says that the sensor is noisy and has a standard deviation of 5°C. What should you believe the temperature is?
You shouldn’t give a single number as an answer, because we are uncertain. Instead, you should give a distribution over the possible true temperatures.
Mathematically, we can represent this as follows. Let $X$ be the random variable corresponding to our observed data, and let $\mu$ be the true temperature. Suppose we believe that the true temperature $\mu$ is probably around 5°C this time of year but we are reasonably uncertain, i.e. we have the prior
\[\mu \sim \mathcal N(5, 10)\]Then we model the data as being normally distributed given these parameters:
\[X \mid \mu, \sigma \sim \mathcal N(\mu, \sigma^2)\]We can then use Bayes’ rule to find the distribution of $\mu$ given the observed data:
\[\mathbb P(\mu \mid X = 8, \sigma = 5) = \frac{\mathbb P(X = 8 \mid \mu, \sigma = 5)\mathbb P(\mu \mid \sigma = 5)}{\mathbb P(X = 8 \mid \sigma = 5)}\]@Prove that
\[\mathbb P(A \mid B, C) = \frac{\mathbb P(B \mid A, C)\mathbb P(A \mid C)}{\mathbb P(B \mid C)}\]
i.e. the form of Bayes’ law where you maintain one of the conditions.
There are specific names for each of these terms:
- $\mathbb P(X = 8 \mid \mu, \sigma = 5)$ is the likelihood of the data, how likely it was to see the data given the parameters
- $\mathbb P(\mu \mid \sigma = 5)$ is the prior, representing what we believed about $\mu$ before seeing the data
- $\mathbb P(X = 8 \mid \sigma = 5)$ is the model evidence, representing how likely we were to see $X = 8$ over all choices of $\mu$
- $\mathbb P(\mu \mid X = 8, \mu = 5)$ is the posterior distribution, how our estimate of $\mu$ has updated given the evidence
More generally if we observe multiple temperatures $\mathcal D = { 13, 8 }$, then we can recursively apply Bayes rule:
\[\mathbb P(\mu \mid \mathcal D = \{13, 8\}, \sigma = 5) = \frac{\mathbb P(\mathcal D = \{13\} \mid \mu, \mathcal D = \{8\}, \sigma = 5)\mathbb P(\mu \mid D = \{8\}, \sigma = 5)}{\mathbb P(\mathcal D = \{13\} \mid \mathcal D = \{8\}, \sigma = 5)}\]All models make assumptions
All machine learning models, even the “non-Bayesian” ones, make assumptions about the process the underlying process that was used to generate the data. In Bayesian probabilistic modelling, we aim to make these assumptions explicit, and infer the underlying process that generated the data.
One of the ways to do this is by describing the “generative story” of the data; a description of the process which actually generated the observations we see.
Gaussian density estimation
Now consider the more general setup where have been told that some data $x _ 1, \ldots, x _ N$ were generated from a Gaussian distribution with an unknown mean $\mu$ and a known variance $\sigma^2 = 1$. We observe $x _ 1, \ldots, x _ 5$, and we aim to predict what the value of $\mu$ is given these observations.
The generative story is as follows:
- Nature selects some parameters $\mu, \sigma$ (which we aim to infer)
- Given these parameters, each observation is sampled from $x _ n \sim \mathcal N(\mu, \sigma^2)$ for $n = 1, \ldots, N$
- We observe the resulting dataset $\mathcal D = {x _ 1, \ldots, x _ n}$
Pictorially, this can be represented via plate diagram (see [[Notes - Uncertainty in Deep Learning MT25, Probability reference]]U):
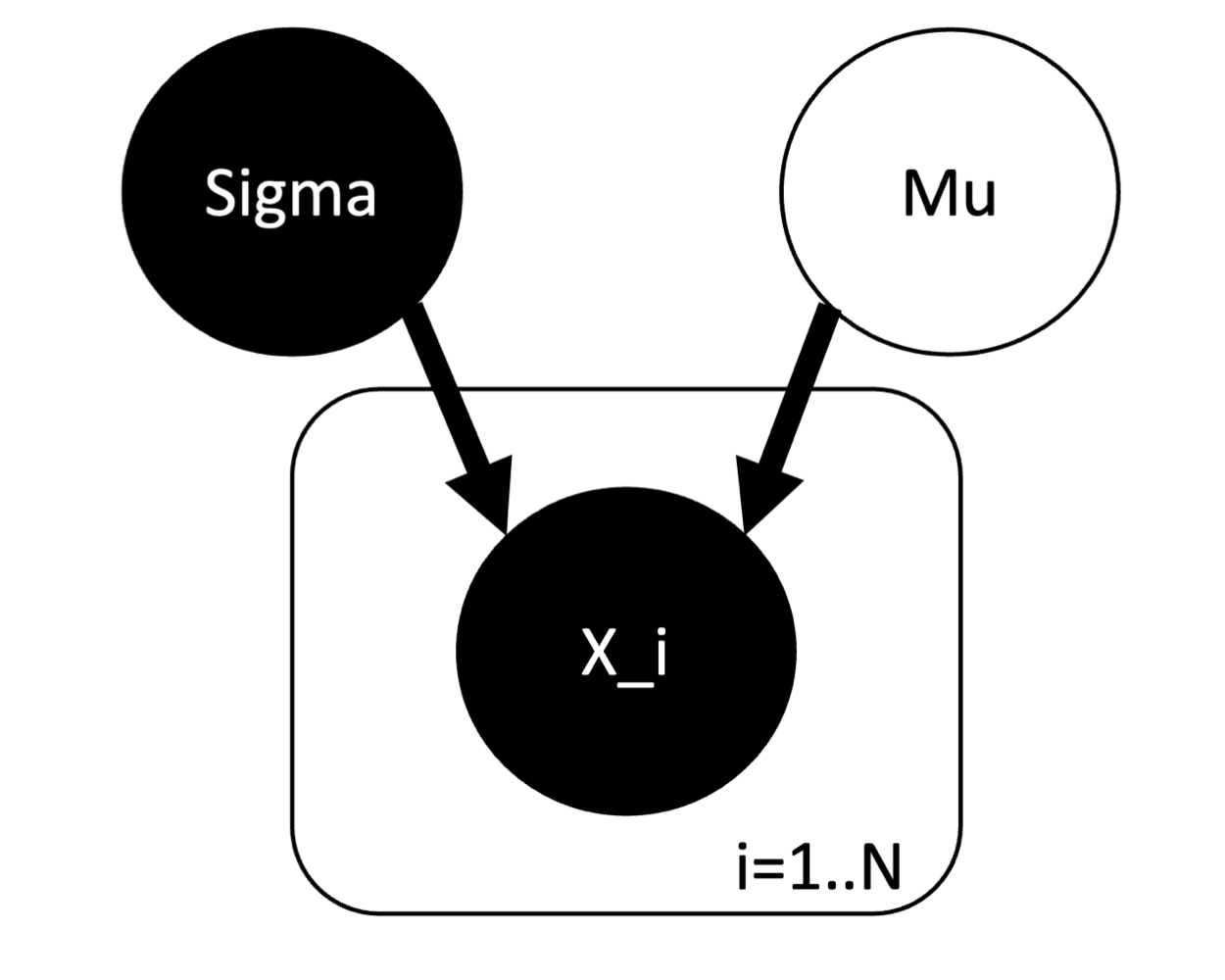
where:
- Circles represent random variables
- Plates represent repetition
- Black represents observed quantities
- White represents unobserved quantities
- Arrows represent condition dependence
Applications of the laws of probability give us the convenient formula for the joint distribution
\[\begin{aligned} \mathbb P(\mathcal D = \{x_1, \ldots, x_N\}, \mu, \sigma) &= \mathbb P(\mathcal D \mid \mu, \sigma) \mathbb P(\mu) \mathbb P(\sigma) \\ &= \left( \prod^N_{i = 1} \mathbb P(x_i \mid \mu, \sigma) \right) \mathbb P(\mu) \mathbb P(\sigma) \end{aligned}\]To actually be able to use this distribution, we need some extra details in the form of priors. We will assume that $\mu \sim \mathcal N(0, 10)$ and $\sigma = 1$. Then we may actually calculate that
\[\mathbb P(\mathcal D = \{x_1, \ldots, x_N\}, \mu, \sigma) = \left( \prod^N_{i=1} \mathcal N(x_i \mid \mu, 1) \right) \mathcal N(\mu \mid 0, 10)\]Generative part of a variational autoencoder
For a more complicated example, consider the generative story of a variational autoencoder. A variational autoencoder is a Bayesian probabilistic model that replaces simple Gaussians with neural networks that parameterise the distributions.
- Nature selects parameters $\mu _ n \in \mathbb R^{10}$, $\sigma _ n \in \mathbb R^+$ for $n = 1, \ldots, N$ and some decoder function $f : \mathbb R^{10} \to X$, where $X$ is the output space.
- We generate $N$ latent points $z _ n \sim \mathcal N(\mu _ n, \sigma _ n^2)$, these represent hidden, unobserved factors of variation
- We generate an observation from these data points, $x _ n \sim \mathcal N(f(z _ n), I)$
- We observe $f, \mathcal D = {x _ 1, \ldots, x _ N}$
As a plate diagram, we have:
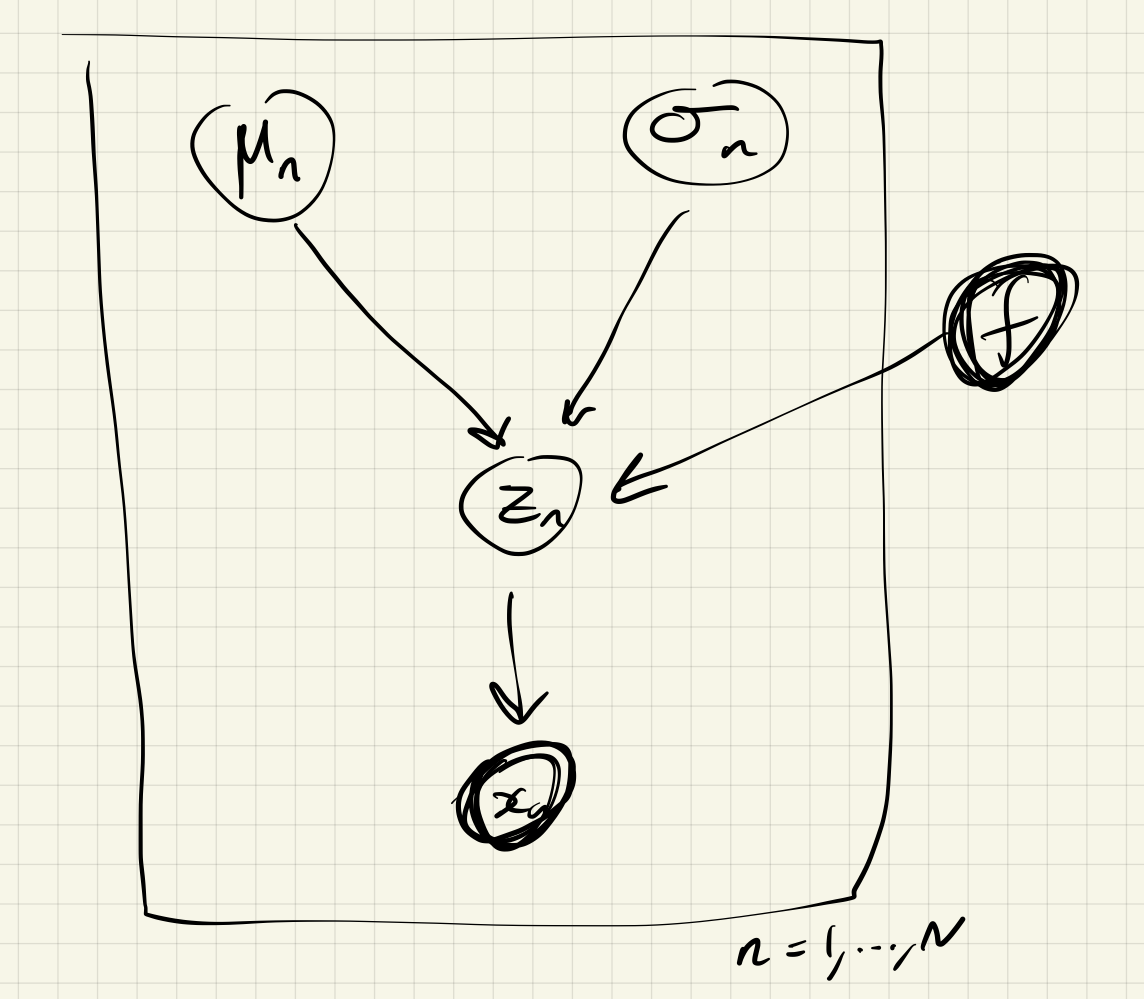
(this plate diagram also assumes all $\mu _ i$ and $\sigma _ i$s are selected independently, which is not explicitly stated in our assumptions, but is in our plate diagram).
and assuming that we have priors $\mu _ i \sim \mathcal N(0, 10)$ and $\sigma _ i \sim \mathcal N(0, 10)$, we obtain the following factorisation of the joint distribution:
\[\begin{aligned} \mathbb P(x, z, \mu, \sigma, f) &= \mathbb P(x, z, \mu, \sigma \mid f) \mathbb P(f) \\ &= \mathbb P(f) \prod^n_{i=1} \mathbb P(x_i, z_i, \mu_i, \sigma_i \mid f) \\ &= \mathbb P(f) \mathbb P(z, \mu, \sigma) \prod^n_{i = 1} \mathbb P(x_i \mid z_i, \mu_i, \sigma_i, f) \\ &= \mathbb P(f) \prod^n_{i = 1} \mathbb P(x_i \mid z_i, f) \mathbb P(z_i \mid \mu_i, \sigma_i) \mathbb P(\mu_i, \sigma_i) \\ &= \mathbb P(f) \mathbb P(\mu, \sigma) \prod^N_{i=1} \mathbb P(x_i \mid z_i, f) \mathbb P(z_i \mid \mu_i, \sigma_i) \\ &= \mathbb P(f) \prod^N_{i = 1} \mathbb P(x_i \mid z_i, f) \mathbb P(z_i \mid \mu_i, \sigma_i) \mathbb P(\mu_i) \mathbb P(\sigma_i) \end{aligned}\]In practice, the goal of a variational autoencoder is to figure out what $f$ is rather than just to write down this distribution.