About this website

Created: July 28, 2024
Updated: October 11, 2024

Welcome… again!

You’ve probably just landed here from the front page, or from another post where I’ve linked this as a reference on how to get around. Hello! This post serves as a high-level index of everything on this site, an explanation of how it gets built, and a home for a few visualisations of the content on here (including what pretty shapes you get when projecting the embeddings of every page down into 3D).

Motivation

Why have a site like this? One reason is the idea of “digital gardening”: just as cultivating a small patch of the real world is something people can find very fulfilling, so is cultivating a small patch of the internet. Digital gardens are like a cross between a blog and a wiki, a loose space for working with the garage door up. The garden metaphor stretches quite far: just how real gardens can be messy if you don’t look after them, so can digital gardens. For more on digital gardening, see this great essay by Maggie Appleton.

Writing about what I’m learning and organising all of this content is something I find really enjoyable, even if I’m ultimately just organising it for myself (and bots). But if anyone else finds anything useful or interesting, that’s also great.

A whistle-stop tour

Everything on this site is organised into four main sections:

Blog posts

As of right now (August 4th 2024) this section is a bit empty – the last proper blog post I wrote was [[Analytics with Caddy and Shynet]]B back in early 2022 and that was on the old version of my site. There’s also a few more from back then, like [[Can you ever draw in 3D noughts and crosses?]]B.

Hopefully in a year I’ll have a bit more to say here. I’m a big fan of a service called Beeminder, which allows you to create “commitment contracts”: do $X$ or get charged $£Y$. My personal beeminders are in [[Beeminders]]M; there I’ve set one up which will charge me £5 every week that I don’t publish a blog post. Although I am planning on reducing the frequency of this when I head back to university in October.

Here’s what I’m planning on working on:

  • [[FRACTRAN and theoretically cheating at your A-levels]]B: I also started this post back in early 2022, and it’s partially completed already. The idea is that by using a very specific sequence of instructions, you can get a scientific calculator to do arbitrary computation, even if that calculator is “non-programmable”. The technique used to do this is related to a very interesting and pretty programming language called FRACTRAN, invented by John Conway (famous also for the game of life).
  • [[Unusual running challenges]]B: The title definitely needs some work. This one is about some unusual running challenges, some arbitrary like “run 5K, but backwards”, and some not, like applying graph theory to your local road network for mathematically optimal exercise (optimal in terms of a specific math problem, not guaranteed to be optimal in terms of fun).
  • [[Film photography around Oxford]]B: Around this time last year, I got interested in amateur film photography (as well as other retro activities, like trying not to spend 3h+ on my phone every day). These are the best of the photos I took while at uni – though unfortunately my analog days have come to an end after I dropped my camera down a flight of stairs.

Notes

University/A-Level Notes

The other key part of this site is a place for my notes from university and A-Levels to live:

I really like seeing how going to university has “turned up the resolution” for my notes on lots of different topics. In my A-Level notes on finite state machines above, I have things like:

(A-Level): What is a finite state machine?

An abstract model of computation that is used to model logic.

but after taking [[Course - Models of Computation MT23]]U, I can have things like:

(University): Can you give the formal definition of a DFA?

A 5-tuple $(Q, \Sigma, \delta, q _ 0, F)$ where

  • $Q$ is a finite set of states
  • $\Sigma$ is a finite set called the “alphabet”
  • $\delta : Q \times \Sigma \to Q$ is the transition function
  • $q _ 0 \in Q$ is the start state
  • $F \subseteq Q$ is the set of accepting states

For more detail on my note taking process, there’s some explanation in [[University Notes]]U. I am particularly happy with my notes for:

Personal Notes

Alongside my university and A-Level notes, I also have notes on other things I have found interesting. These are mostly organised in the following entries:

Misc

This category holds all of the content that doesn’t really fit into one of the other categories. This lives in [[Misc]]M. There’s not many pages like this, so I can list them all here:

How it works

This site and the notes on are built from a big mishmash from lots of great tools:

  • Obsidian, a closed-source notes app.
  • Building the site
    • obsidiantools, a Python library for interacting with Obsidian.
    • Jekyll, a static site generator written in Ruby.
    • al-folio, a very popular Jekyll theme.
  • Flashcards

Writing notes

I take all my notes in Obsidian, which is a closed source notes app. It might be closed-source but it is free and is the best note taking app I have used. Unlike some alternatives like Joplin or Roam with store notes in arcane SQLite databases, Obsidian is just a skin over a folder of markdown files.

This means that for example my notes for [[Part A]]U are just a folder on my computer (here only shown two levels deep):

.
├── Part A.md
├── exams
│   ├── list
│   ├── papers
│   └── questions-to-review
├── ht24
│   ├── ads
│   ├── courses
│   ├── gdp
│   ├── numerical-analysis
│   ├── quantum-information
│   └── rings-and-modules
└── mt23
    ├── complex-analysis
    ├── courses
    ├── linear-algebra
    ├── machine-learning
    ├── metric-spaces
    └── models-of-computation

Why use a closed-source skin over a folder of markdown files rather than just editing the files in a text editor? I also did this for 2 years using Vim and a program I wrote called albatross, but the experience using Obsidian is considerably smoother since it natively handles things like displaying images and keeping track of the links between all the files. Doing all of this with a Vim took a lot of effort.

Since all my notes are just folders of markdown files, they are naturally organised into a tree structure like you can see above. But Obsidian also lets you create wikilinks, which are inter-note links [[enclosed in square brackets]] – this is what all of the colourful links are. This means that your notes are also organised into a (directed) graph where each node is a file, and two nodes are connected is there is a wikilink from one to the other.

Building the site

To actually build this website, I use a popular static site generator written in Ruby called Jekyll. Jekyll builds static sites from folders of markdown files, which is great, but there’s quite a bit of processing that needs to be done so that Obsidian and Jekyll can work nicely with each other. This includes:

  • Filtering out notes I don’t want to be included
  • Being able to recognise [[wikilinks]], which Jekyll doesn’t natively understand
  • Putting posts into categories
  • Deciding on paths
  • Parsing flashcards so that they can be rendered nicely
  • Performing special processing for things like the home page or [[Bookshelf]]N
  • Calculating semantic embeddings for each post using the Sentence Transformers library
  • …fixing some more very specific interoperability issues, like how underscores have to be escaped in Obsidian math blocks.

This is all done with a library called obsidiantools and a hacky Python program which will spit out a _posts folder Jekyll can convert into a site using the al-folio theme. There’s a few extra custom things done here like rendering flashcards and wikilinks, but the majority of the heavy lifting is done by Jekyll and al-folio.

Old website

This website replaces my old website which is frozen in time as of mid 2022. It had a very similar layout, but was built using Hugo with the hugo-eureka theme rather than Jekyll.

Flashcards: Anki and spaced repetition

The main way in which I take notes is by making flashcards. These look like this:

What is a flashcard?

A question-and-answer pair.

Like the rest of the site, these are also written entirely in Markdown, using syntax like

<-- flashcard -->
What is a flashcard?::
A question-and-answer-pair
<-- flashcard-end -->

Then there’s a plugin for Obsidian called Obsidian-Anki-Sync which will go through all my notes, parse these blocks, and sync them with Anki. Then every morning I’ll be given a list of flashcards to attempt, picked by Anki in a way it thinks is best for getting information into long term memory. This way I can memorise lots of important stuff that I’ll need to know in an exam.

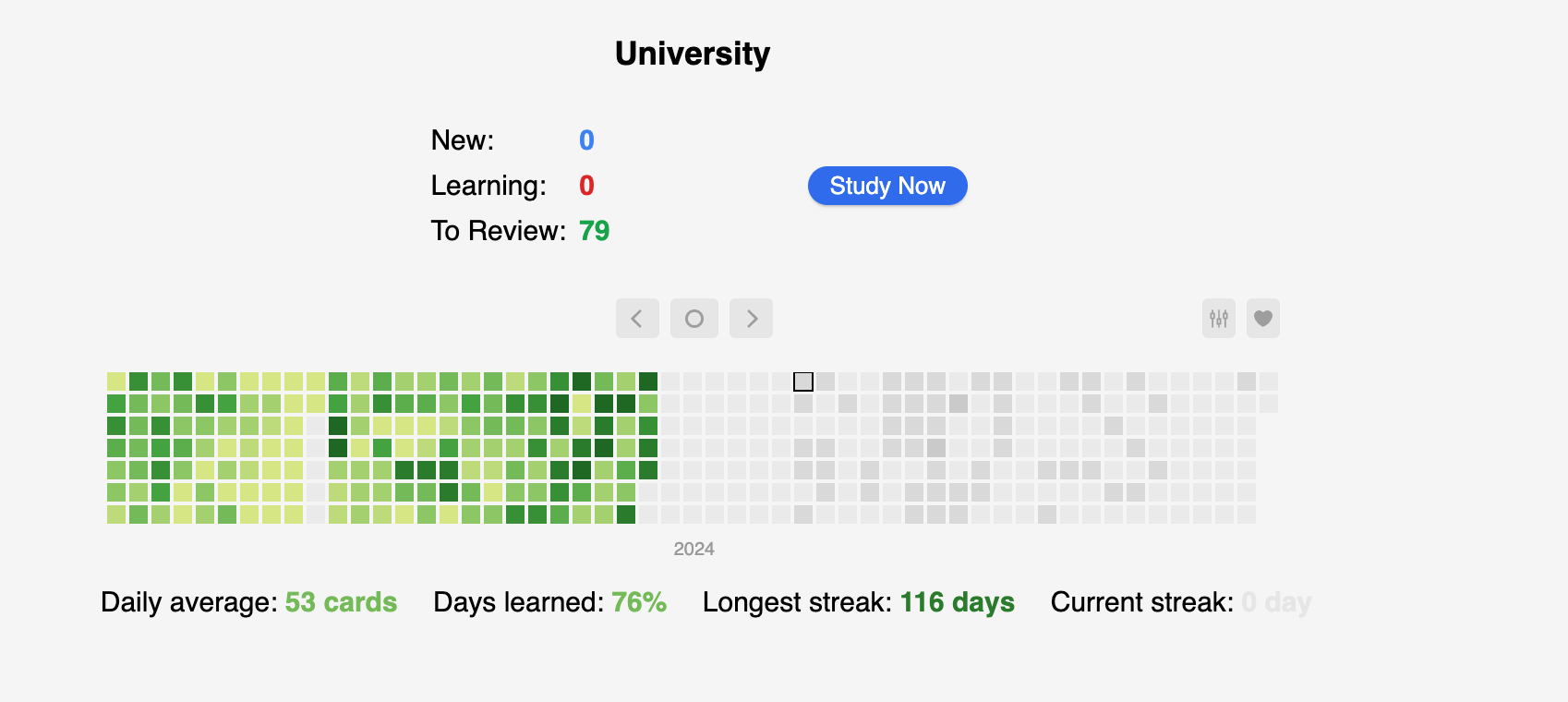
(this is what Anki looks like, each square is a day. The darker it is, the more cards I reviewed on that day).

I used to have the philosophy that flashcards should be super short and concise, and this view was spurred on by great essays like What are the most important attributes of good spaced repetition memory prompts? and Augmenting Long-term Memory. Over time, I’ve become less hardcore about this, now I might make a flashcard for a proof that takes about 10 minutes to complete so that I can learn it semi-rote using Anki. This isn’t really what Anki is used for, but it is useful for exams. The best solution might be a piece of software specifically designed for practicing proofs / questions, I tried something similar for A-levels with a project called Sergeant, but this isn’t perfect.

One more thing about flashcards: I think there’s a lot of value just in creating flashcards even if you never review them, since the process of just compressing and reformulating the information is very useful, especially if the source material is not great.

Conclusion: A bird’s-eye view using machine learning

As part of the processing when this site is built, “embeddings” are calculated for each post using the Sentence Transformers library. This converts each post into a 384-dimensional vector which is a numerical representation of the underlying meaning of the text. This means that posts with similar embeddings (in the sense of cosine similarity) end up being semantically similar: e.g. the blog post [[Can you ever draw in 3D noughts and crosses?]]B is quite close to [[Lecture - Functional Programming MT22, XIII]]U, since that lecture was about implementing Countdown in Haskell, and both noughts & crosses and Countdown are games. This is what creates the “Related posts” section at the end of each page.

The fun part is that you can then project these 384-dimensional vectors into 3-dimensional space using a technique called principal component analysis. This visualisation does exactly that. If you look around, you might be able to spot interesting clusters of similar notes: one for analysis, one for algebra, one for blog posts, and so on.



Though not interactive, I’ve also done the same thing but where I’ve included all of my private notes. These notes are in black.

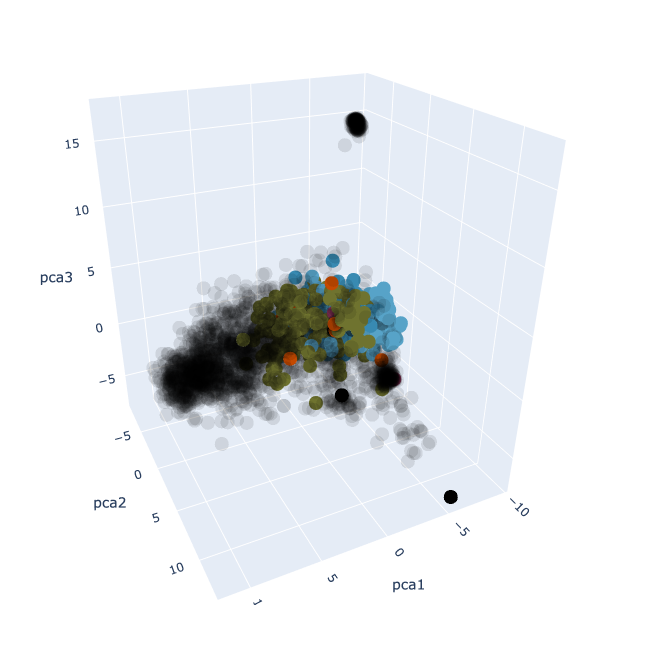
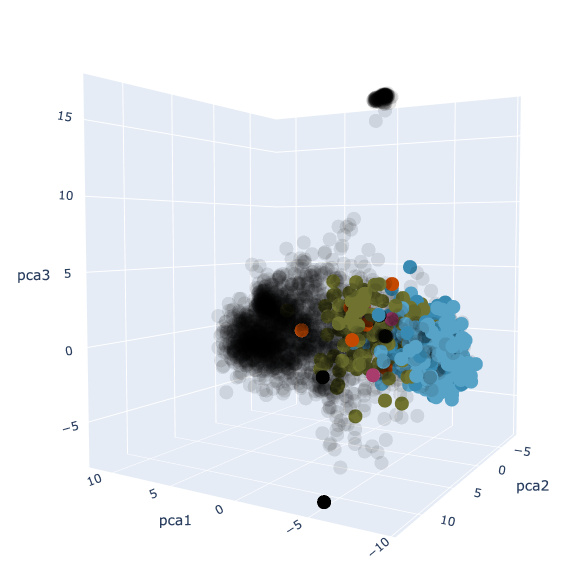
As a consequence of how PCA works (see [[Notes - Machine Learning MT23, Principal component analysis]]U if you’re interested), adding in my private notes will change the locations of all the existing points, so it won’t look the same as it does in the visualisation above.

I hope you have fun looking around!



Related posts