A Dangerous Way of Taking Derivatives
Or, “This One Funky Trick For Taking Derivatives That Teachers Don’t Want You To Know”.
The gradient of a straight line
Finding the gradient of a straight line is pretty easy. For example, consider the following straight line:
\[y = 3x + 1\]In this case, the gradient is three. If it were $-5x$ instead of $3x$, it would be $-5$. In general, the gradient of a straight line $y = mx+c$ is just the value of $m$. This follows from the limit definition of the derivative:
\[f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}\]In this case,
\[f(x) = mx + c\] \[\begin{aligned} f(x + h) &= m(x + h) + c \\\\ &= mx + mh + c \end{aligned}\]And so overall
\[\begin{aligned} f'(x) &= \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \\\\ &= \lim_{h \to 0} \frac{mx + mh + c - mx - c}{h} \\\\ &= \lim_{h \to 0} \frac{\cancel{mx} + mh + \cancel{c} - \cancel{mx} - \cancel{c}}{h} \\\\ &= \lim_{h \to 0} \frac{mh}{h} \\\\ &= m \end{aligned}\]Taking the derivative dangerously
This has all been safe so far. But what about if instead of $m$ being a constant, like $3$ or $5$, it was actually a function of $x$? Our straight line formula would now become
\[y = m(x)x + c\]I’m so used to taking the value before $x$ as the derivative that my intuition is that the value of $m(x)$ at some point $x = a$ must be the derivative of $f(x)$ at that point. You can even argue it in a hand-wavy geometric sense; the derivative is the ‘gradient’ of the curve at a certain point and picking different values for $a$ gives a family of straight lines each corresponding to the slope of the function at different points.
For example, if we wanted the straight line corresponding to the function at the point $x = 1$, we might make something like this:
\[y = m(1)x + c\]And since $m(1)$ or $m(a)$ is a constant, this must be the gradient, right? Hmmmm. Something seems strange but I’m not sure I can completely understand why. How about the limit definition of a derivative? With one small mistake, this says that it’s true too:
\[\begin{aligned} f(x) &= m(x)x + c \\\\ \\\\ f(x + h) &= m(x)(x+h) + c \\\\ &= m(x)x + m(x)h + c \\\\ \\\\ f'(x) &= \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \\\\ &= \lim_{h \to 0} \frac{m(x)x + m(x)h + c - m(x)x - c}{h} \\\\ &= \lim_{h \to 0} \frac{\cancel{m(x)x} + m(x)h + \cancel{c} - \cancel{m(x)x} - \cancel{c}}{h} \\\\ &= \lim_{h \to 0} \frac{m(x)h}{h} \\\\ &= m(x) \end{aligned}\](here, the mistake is not changing $m(x)$ to $m(x + h)$ in the expression for $f(x+h)$).
Why isn’t this true?
The fact this isn’t true becomes a lot more obvious when you consider that any function can be put in the form
\[y = m(x)x + c\]For example, consider $f(x) = e^x$. To put into this “straight-line” form, all you need to do is set $c = 0$ and make $m(x) = e^x/x$:
\[y = \frac{e^x}{x} x\]But the derivative of $f(x) = e^x$ is not $\frac{e^x}{x}$, it’s just $e^x$. You could even put $\sin(x)$ into this form:
\[y = \frac{\sin(x)}{x} x\]Again, the derivative of $\sin(x)$ is not $\frac{\sin(x)}{x}$ but $\cos(x)$. In general, any function $f(x)$ can be put into this format just by dividing by $x$ and putting it as the ‘coefficient’ of $x$.
\[y = \frac{f(x)}{x} x\]This, along with a geometric picture, makes it clear why this wrong. You normally calculate gradients using the ratio of the change in $y$, $\Delta y$, and the change in $x$, $\Delta x$.
\[\begin{aligned} m &= \frac{\Delta y}{\Delta x} \\\\ &= \frac{y_1 - y_0}{x_1 - x_0} \end{aligned}\]When you’re dividing by $x$ to get $\frac{f(x)}{x}$, it’s like you’re calculating the gradient of the straight line passing through the function at some point $x$ and the origin:
\[m = \frac{f(x) - 0}{x - 0}\]But the limit definition of the derivative is about considering how a small change in $x$ corresponds to a small change in $y$, so that $x _ 1$ and $x _ 0$ are very close together. Doing it this way is like considering the ratio of the change in $y$ to the change in $x$ across the entire function so far, moving all the way from the origin to a point $x$ instead of moving from a point very close to $x$.
Here’s the straight line passing through $\sin(x)$ at some point with the gradient calculated using the dangerous way:
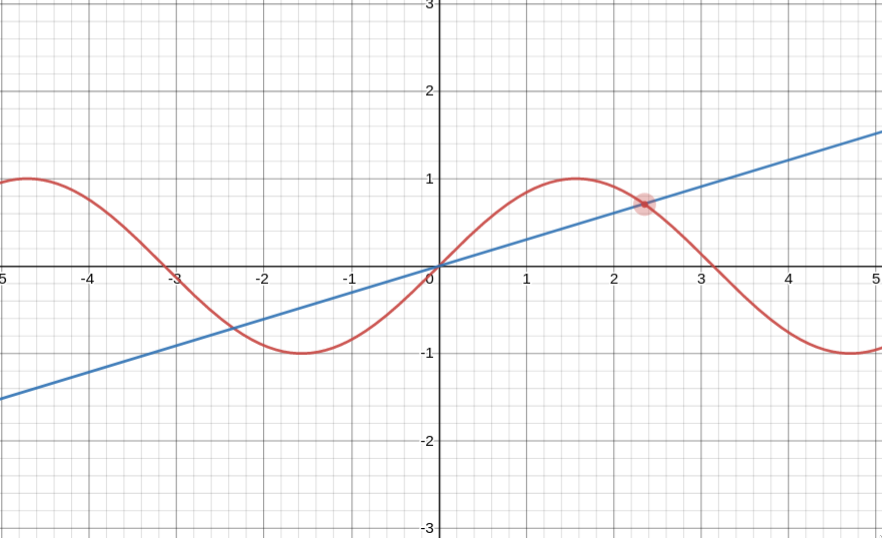
And here it is with the actual tangent at that point:
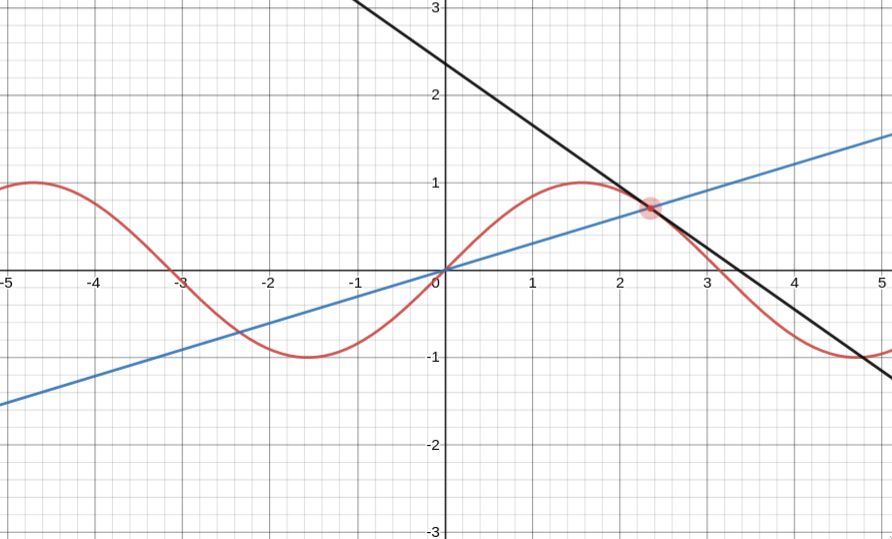
As you can see, the straight line with gradient just $m(x)$ (blue) passes through the origin, whereas the straight line with gradient $f’(x)$ (black) is tangent to the curve at that point. Clearly the black line much better encompasses the idea of the slope of a function.
When are you allowed to take the derivative dangerously?
So why does this work for straight lines? You could think of like a differential equation. When working out the gradient of a line like $y = mx + c$, you extract the gradient by first subtracting by $c$ and then dividing by $x$. In other words,
\[m = \frac{y - c}{x}\]We can use calculus to ask the question “for which functions is the gradient equal to what you get by subtracting $c$ and dividing by $x$?”:
\[\frac{\text{d}y}{\text{d}x} = \frac{y - c}{x}\]Separating the variables:
\[\frac{1}{y - c}\frac{\text{d}y}{\text{d}x} = \frac{1}{x}\]Integrating with respect to $x$ on both sides:
\[\int \frac{1}{y - c} \frac{\text{d}y}{\text{d}x} \text{d}x = \int \frac{1}{x} \text{d}x\]The derivative of $\ln(y - c)$ is equal to $\frac{1}{y-c}\frac{\text{d}y}{\text{d}x}$ by the chain rule, and as integration is the reverse of differentiation, it just becomes:
\[\ln(y - c) = \ln(x) + A\]Where $A$ is the constant of integration (the constants of integration from both sides can be combined into one as adding two constants together is still just one constant). Finally, exponentiating both sides:
\[\begin{aligned} e^{\ln(y - c)} &= e^{\ln(x) + A} \\\\ y - c &= e^Ax \\\\ y - c &= mx \\\\ y &= mx + c \\\\ \end{aligned}\]($e^A$ is just another constant which we are conveniently calling $m$). What this says is that the only functions where it’s valid to take the derivative the dangerous way is when they are of the form
\[y = mx + c\]which is just the formula for a straight line! Magic!
Conclusion
Why write this? I’m not sure. I just thought it was interesting how I’m so used to just writing down the derivative of a straight line as “the bit before $x$” that it’s hard to resist the dangerous idea that if there’s a function $m(x)$ before $x$, then that’s also the derivative.
And it’s cool how you can ask the question “when are you allowed to do this?” and the rules of calculus tell you that it’s only ever true for straight lines.