Can you ever draw in 3D noughts and crosses?

• The game
• No fun
• The question
• Showing there’s no draws
  • Representing the board
  • Checking for winners
  • Crunching the numbers
• Conclusion
• Footnotes

⚠️ As it stands, while the conclusion is true (there is no possibility of a draw), the argument used to get there in the “Crunching the numbers” section is not correct.

TLDR: No, you can’t.

The game

3D noughts and crosses, or 3D tic-tac-toe, is a variant of tic-tac-toe where you play on a $3 \times 3 \times 3$ cube. It’s easiest to represent this with three separate grids, where you can win in each grid individually but also get diagonals and straight lines through the cube. Here’s three different games, in three different columns:

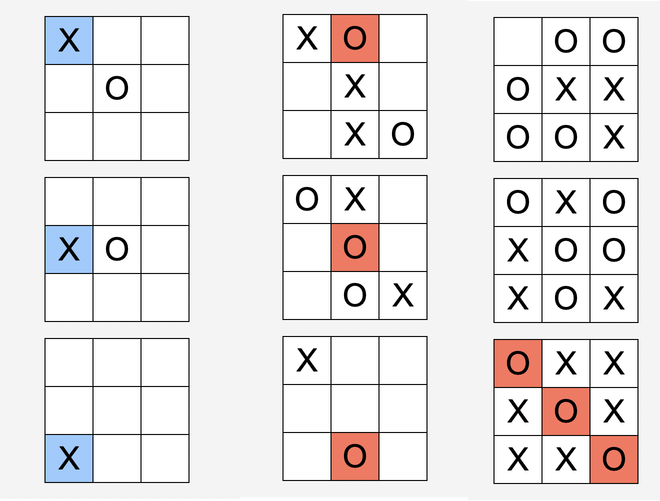
The first shows a pretty clear win from $X$. The second is a more complicated game where $O$ wins, and the final is a game where the two players are cooperating in order to try make the game go on for as long as possible. If you want to try play for yourself, I’ve been procrastinating doing A-level coursework and working on this website instead.

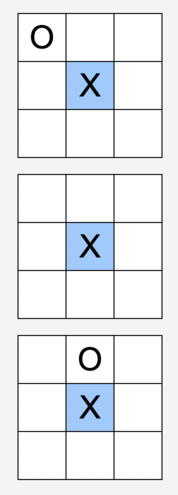
When you first play it, there’s a few ways you can win that are a little unintuitive. Here’s two more ways you can get a line through the cube which might be a little hard to spot, one on the left and one on the right:

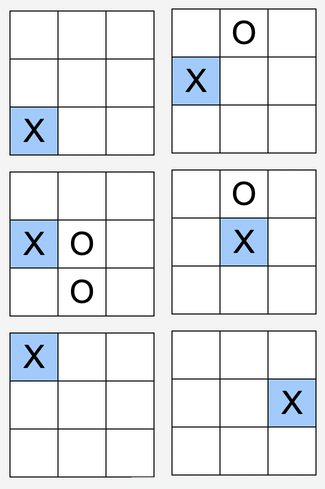
If the three grids represent the three layers of the cube extending upwards and layered top-to-bottom as shown, then the left side represents a line starting in the bottom-top-left and extending to the upper-bottom-left at the back of the cube. The right side represents a line ranging from the middle-bottom-right of the first face to the middle-bottom-left of the last face.

No fun

If you’ve played normal noughts and crosses for more than two minutes, it quickly becomes clear that the game will always end in a draw unless either player makes a mistake early on. For 3D noughts and crosses, the situation is even worse, because it becomes clear that the $X$ player can easily force a win by playing in the very centre square:

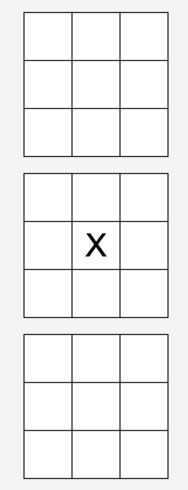
From this point onwards, $O$ can’t do anything to win or even draw. It’s not even like the $X$ player needs to be super smart and think several moves ahead: the $O$ player is stuck in a situation where it keeps having to block $X$’s attack, until a situation is reached where it would need to block the attack in two places, leading to a sad, but predetermined loss.

There are several ways you might consider trying to make the game fairer¹:

• Prevent the first player from taking the centre square. If you adopt this rule, the second player can easily force a win.
• Ban the centre square altogether. This has no effect, the game can still easily be won by the first player.
• Pick who goes first randomly. This means its fair, but is no better than flipping a coin because the first player can always win.

The only real solution is to introduce a third player, which means that the perfect game can be played out until a draw kind of like in ordinary noughts and crosses. And if you are allowed to include more dramatic variants, there is:

• Quantum tic-tac-toe, which introduces the idea of superposition, entanglement and collapse into normal tic-tac-toe,
• 4D tic-tac-toe, which uses a $4\times 4\times 4\times 4$ hypercube rather than a $3 \times 3 \times 3$ cube that I’m talking about here. Also interesting is just using a $4 \times 4 \times 4$ cube (no fourth dimension), this has the same flavour as 3D noughts and crosses but doesn’t seem to immediately lead to a win for either player.

The question

So it seems that it’s a lot easier for a player to win in this variant of noughts and crosses. In fact, if you play the game a few times, even deliberately badly, you will notice that there never seems to be a draw. A question you might ask is:

Can you ever draw in 3D noughts and crosses?

That is, is there some arrangement of $X$s and $O$s on the board such that the board is full and no player wins? The answer turns out to be no.

Showing there’s no draws

Showing that there is no way to draw in 3D noughts and crosses is actually a fun programming problem. If you want to give a go yourself, you might break it down into three stages:

• Representing the board
• Checking for winners
• Considering all possible games

For a hint for how to check for winners, consider how you’d check for winners in a normal tic-tac-toe game, and then about how you could reuse the same code for checking for wins in three dimensions with a slight change.

Representing the board

Let’s assume that the board information is laid out as a 2-dimensional array.:

[
  [None, None, None, None, None, None, None, None, None],
  [None, None, None, None, None, None, None, None, None],
  [None, None, None, None, None, None, None, None, None],
]

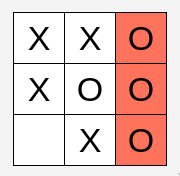
Each sub-array corresponds to the marks in each sub-grid indexed from $0$ and starting at the top left. For example, position $[1][3]$ would refer to the fourth square in the second grid. We’ll use None to represent an empty square, and "O” and "X" to represent a nought or a cross respectively. For example, the array

["X", "X", "O", "X", "O", "O", None, "X", "O"]

corresponds to a grid that looks like this:

Three of these together are enough to make up the state of the whole board. You could use a 3-dimensional array corresponding to the 3 dimensions of the cube, but this is unnecessary and makes the code for finding winners more complicated than necessary.

Checking for winners

One way to check for winners in ordinary tic-tac-toe is to use a list of all winning positions like this one:

winning_positions = [
    [0, 1, 2],
    [3, 4, 5],
    [6, 7, 8],
    [0, 3, 6],
    [1, 4, 7],
    [2, 5, 8],
    [0, 4, 8],
    [2, 4, 6],
]

Here, each list represents three positions that will lead to a win if the same player has all three of them. For example, the top list [0, 1, 2] corresponds a player getting three in a row at the top of the grid. Checking for a winner is then as simple as iterating through this list and checking if the same player has a mark at all three locations.

We can use this same idea to check for winners in 3D noughts and crosses. As each of the three sub-grids can also be won in the same way as normal tic-tac-toe game, a good place to start would be checking if anybody has won in of the three grids. In Python, it might look like this:

for gridIndex, grid in enumerate(grids):
  for position in winning_positions:
    i, j, k = position

    # Check all three grid positions are occupied by the same player
    if grid[i] == grid[j] and grid[j] == grid[k] and grid[i] != None:
        return True

Another way someone might be able to win is by getting a line straight through the cube, like the middle square on all three grids:

Checking for this type of win is also simple: iterate through the numbers $0$ to $8$ and check if a player has a mark in that location across all three grids. Again, the code might look like this:

for i in range(9):
  if grids[0][i] == grids[1][i] and grids[1][i] == grids[2][i] and grids[0][i] != None:
    return True

The most complicated bit is detecting wins that span across the three layers of the cube and aren’t as simple as straight lines through the same piece. Luckily, we can use the winning_postions list again to make this process easier. Wins “through” the cube must follow the same pattern as wins on an individual layer, but you’re increasing the depth with each position that you check.

For something like [0, 4, 8] on one grid, you’d now have to check that the same player has a mark in location 0 on the first grid, 4 on the second grid and 8 on the final grid. You’d also have to check the reverse: if a player got position 8 on the first grid, 4 on the second grid and 0 on the final grid, it would be the same but the direction of the diagonal would change.

Here’s a more visual illustration for the same [0, 4, 8] pattern:

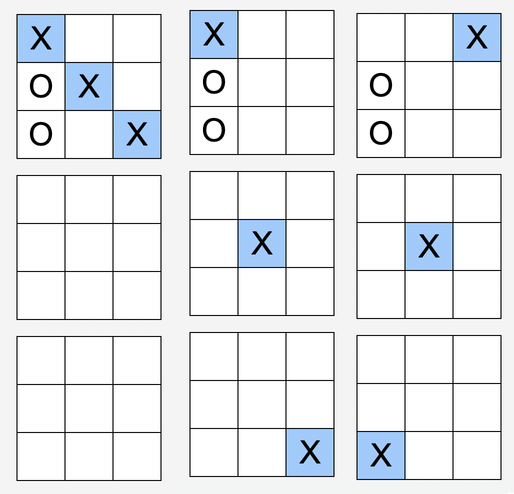
The code for this might look something like this:

for position in winning_positions:
  i, j, k = position

  if grids[0][i] == grids[1][j] and grids[1][j] == grids[2][k] and grids[0][i] != None:
    return True

  if grids[0][k] == grids[1][j] and grids[1][j] == grids[2][i] and grids[0][k] != None:
    return True

And with that third check, the algorithm for checking for a winner in 3D noughts and crosses is complete. Overall, the code looks something like this:

# assumes grids is a global variable
def check_winner():
  for gridIndex, grid in enumerate(grids):
    for position in winning_positions:
      i, j, k = position

      if grid[i] == grid[j] and grid[j] == grid[k] and grid[i] != None:
        return True

  for position in winning_positions:
    i, j, k = position

    if grids[0][i] == grids[1][j] and grids[1][j] == grids[2][k] and grids[0][i] != None:
      return True

    if grids[0][k] == grids[1][j] and grids[1][j] == grids[2][i] and grids[0][k] != None:
      return True

  for i in range(9):
    if grids[0][i] == grids[1][i] and grids[1][i] == grids[2][i] and grids[0][i] != None:
      return True

  return False

Crunching the numbers

Now we can use the code to show that there’s no possible states where a draw is reached. To do this, we could check all possible arrangements of $X$s and $O$s on the board which corresponds to $2^{27} = 134,217,728$ states assuming we naïvely pick $X$s or $O$s at random for each spot on the board. We can cut this down by a factor of ten by considering the fact that moves come in pairs, and that $O$s moves will have to be in the 13 spaces left over after $X$ makes 14 moves – this leaves us with $27 \choose 14$ states, which is $20,058,300$.

However, this measures possible states, not possible games. Included in this estimate are games that have $X$ or $O$ winning in multiple places at the same time, which couldn’t come up during normal play. We can deal with this problem and even further cut down on the states we need to analyse by considering the fact that all three of the grids must all be draws themselves, otherwise there would be a winner overall anyway.

Tic-tac-toe draws come in three flavours:

An “arrow”:

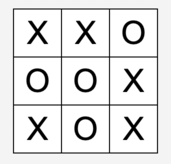
A “scorpion”:

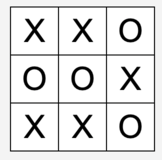
And finally, an “island”:

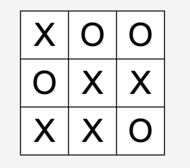
All drawing noughts-and-crosses states are rotations of these three – there’s no other way to draw. That leaves a total of $4\times3 = 12$ different states we can pick from to assign to each individual sub-grid. Since we’re picking three things from a collection of twelve, and it’s with replacement, the number of total possibilities to consider is

Here’s some quick code to get a list of all the possible permutations using itertools and NumPy in Python:

import numpy as np
import itertools

drawing_positions = [
  np.array([["X", "O", "O"], ["O", "X", "X"], ["X", "X", "O"]]), # Island
  np.array([["X", "X", "O"], ["O", "O", "X"], ["X", "O", "X"]]), # Arrow
  np.array([["X", "X", "O"], ["O", "O", "X"], ["X", "X", "O"]]), # Scorpion
]

for i in range(3):
  drawing_positions.append(np.rot90(drawing_positions[i]))
  drawing_positions.append(np.rot90(drawing_positions[-1]))
  drawing_positions.append(np.rot90(drawing_positions[-1]))

perumutations = list(itertools.permutations(drawing_positions, 3))

And finally, we can check all states like so:

count = 0

for perumutation in perumutations:
  grids[0] = perumutations[0][0].flatten() # flatten() is needed because we're using a 1D array for each grid,
  grids[1] = perumutations[1][0].flatten() # but numpy needs a 2D array for np.rot90() to work as we want it to.
  grids[2] = perumutations[2][0].flatten()

  if not is_winner():
    count += 1

print(count)
# Outputs: 0

So there’s no winning combinations! Hence a draw is not possible.

Conclusion

So that’s it – you can never draw in 3D noughts and crosses.

There is some sense in which people wouldn’t see this as a “proof”, in the same way as people rejected a computer-assisted proof of the four colour theorem. Scott Aaronson talks about the role of computers in proof in [[Quantum Computing Since Democritus, Aaronson]]^N:

“…consider the computer proof of the Four-Color Theorem, […]. That proof solved a great, century-old mathematical problem, but it did so by reducing the problem to the tedious enumeration of thousands of cases.”
“What it boils down to, I think, is that there is a sense in which the Four-Color Theorem has been proved, and there’s another sense in which many mathematicians understand proof, and those two senses aren’t the same.”
“For many mathematicians, a statement isn’t proved when a physical process ([…]) terminates saying that it’s been proved – however good the reasons might be to believe that the physical process is reliable. Rather, the statement is proved when they (the mathematicians) feel that their minds can directly perceive its truth.”

There is probably a much shorter combinatorial proof out there that doesn’t require checking all states, but I haven’t been able to think of this yet.

On the website I’ve been working on, there’s an option to “Optimise for game length” which means the AI tries to prevent anyone from winning, including itself. If you turn the depth limit up and get it to play against itself, it can get pretty close to filling up the grid without anyone winning but of course it fails in the last few moves.

Footnotes