Argand Diagrams

Argand diagrams are a way of representing complex numbers by imagining them as points on a plane. In an Argand diagram:

• The $x$-axis is the “real” axis
• The $y$-axis is the “imaginary axis

The complex number $z = x + yi$ can be represented on the diagram by the point $P(x, y)$ where $x$ and $y$ are coordinates. In other words:

• The horizontal position represents the real part of $z$.
• The vertical position represents the imaginary part of $z$.

However! That’s just part of the story. Representing complex numbers as a pair of co-ordinates is kind of analogous to vectors, where you move a certain amount along the x axis and then a certain amount along the y axis. What could another representation of the same idea be? Instead of encoding the information as two movements, one along and one up, you could also conceptualize it as a rotation followed by a displacement.

Think of it like a triangle:

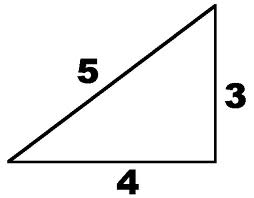
Using the $4+3i$ representation is like moving along $4$ and up $3$, and the “distance” to the point is $5$. The angle from the bottom (in this case the real axis), is $tan^{-1}(\frac{3}{4})$, or $36.87^{\circ}$. So, before we thought about it like this:

• Move along 4
• Move up 3

Now we can think about it like this:

• ROTATE $36.87^{\circ}$
• FORWARD $5$

(In capitals because when the teacher was explaining it to us, he kind of sounded like an army drill seargant telling someone where to go).