Further Maths - Differential Equations
See Also
Flashcards
What type of answer do you normally get for differential equation questions?
A family of curves.
What’s the general process for solving a differential equation question like
\[\frac{dy}{dx} = \frac{y + 1}{x}\]??
- Seperate the two variables and put them on either side of the equation.
- Integrate both sides with respect to $x$.
- Rearrange.
#####
\[\int \frac{1}{y + 1} \frac{dy}{dx} dx\]What does this simplify down to??
\[\int \frac{1}{y + 1} dy\]2021-06-08
What’s the general process for solving a differential equation question like
\[\frac{dy}{dx} = \frac{y + 1}{x}\]
?
- Seperate the two variables and put them on either side of the equation.
- Integrate both sides with respect to $x$.
- Rearrange.
#####
\[\frac{dy}{dx} + P(x)y = Q(x)\]What’s the formula for the integrating factor??
\[e^{\int P(X) dx}\]\[\int \frac{1}{y + 1} \frac{dy}{dx} dx\]
What does this simplify down to?
#####
\[x^2 \frac{dy}{dx} + 2xy = 2x + 1\]How could you rewrite this??
\[\frac{d}{dx}\left(y \cdot x^2\right) = 2x + 1\]#####
\[x^2 e^y \frac{dy}{dx} + 2x e^y = x\]How could you rewrite this??
\[\frac{d}{dx}\left( x^2 e^y \right)\]#####
\[\frac{d}{dx}\left( y^2 \right)\]What’s this equal to??
\[2y\frac{dy}{dx}\]2021-06-09
What’s the general form of differential equation where you can use an integrating factor?
#####
\[e^{\int 2 dx} = e^{2x + c} = Ae^{2x}\]What’s gone wrong working of the integrating factor here?? $c$ has been accounted for but it shouldn’t have been.
2021-06-10
\[\frac{dy}{dx} + P(x)y = Q(x)\]
What’s the formula for the integrating factor?
What does the integrating factor do?
Turns the left-hand side of a differential equation into the “output” of the product rule.
#####
\[a \frac{dy}{dx} + by = 0\]What does the general solution to this look like??
\[Ae^{kx}\]#####
\[a\frac{d^2 y}{dx^2} + b\frac{dy}{dx} + cy = 0\]What does the general solution to this look like??
\[Ae^{\lambda x} + Be^{\mu x}\]#####
\[Ae^{\lambda x} + Be^{\mu x}\]What do $\lambda$ and $\mu$ represent?? Constants to be determined that will solve the differential equation.
#####
\[y = Ae^{\lambda x} + Be^{\mu x}\]What is $\frac{dy}{dx}$??
\[\frac{dy}{dx} = A\lambda e^{\lambda x} + B\mu e^{\mu x}\]#####
\[y = Ae^{\lambda x} + Be^{\mu x}\]What is $\frac{d^2y}{dx^2}$??
\[\frac{d^2y}{dx^2} = A\lambda^2 e^{\lambda x} + B\mu^2 e^{\mu x}\]#####
\[y = Ae^{\lambda x} + Be^{\mu x}\]If you differentiate and substitute this into
\[a\frac{d^2 y}{dx^2} + b\frac{dy}{dx} + cy = 0\]What do you get??
\[Ae^{\lambda x} (a\lambda^2 + b\lambda + c) + Be^{\mu x} (a\mu^2 + b\mu + c) = 0\]#####
\[Ae^{\lambda x} (a\lambda^2 + b\lambda + c) + Be^{\mu x} (a\mu^2 + b\mu + c) = 0\]If this is true, what equations can you write for $\lambda$ and $\mu$??
\[a\lambda^2 + b\lambda + c \\\\ a\mu^2 + b\mu + c\]#####
\[a\frac{d^2 y}{dx^2} + b\frac{dy}{dx} + cy = 0\]What is the “auxillary equation”??
\[am^2 + bm + c = 0\]In the auxillary equation for a differential equation
\[am^2 + bm + c = 0\]What does $m$ represent?? The values of $\lambda$ or $\mu$.
The auxillary equation for a differential equation is
\[am^2 + bm + c = 0\]If
\[b^2 - 4ac > 0\]What does the general solution look like??
\[Ae^{\lambda x} + Be^{\mu x}\]The auxillary equation for a differential equation is
\[am^2 + bm + c = 0\]If
\[b^2 - 4ac = 0\]What does the general solution look like??
\[(A + Bx)e^{\lambda x}\]The auxillary equation for a differential equation is
\[am^2 + bm + c = 0\]If
\[b^2 - 4ac < 0\]What does the general solution look like??
\[Ae^{px}(A\cos qx + B\sin qx)\]Where the roots are $p \pm q$.
2021-07-07
#####
\[a\frac{d^2y}{dx^2} + b\frac{dy}{dx} + cy = f(x)\]Why is this non-homogeneous?? Because it’s equal to a function rather than $0$.
#####
\[a\frac{d^2y}{dx^2} + b\frac{dy}{dx} + cy = f(x)\]What two things do you need to add together to solve this for $y$??
- The complementary function
- The particular integral
\[x^2 \frac{dy}{dx} + 2xy = 2x + 1\]
How could you rewrite this?
If
\[f(x) = p\]What is the particular integral??
\[y = \lambda\]If
\[f(x) = 10\]What is the form of the particular integral??
\[y = \lambda\]If
\[f(x) = p + qx\]What is the particular integral??
\[y = \lambda + \mu x\]If
\[f(x) = 3x + 2\]What is the form of the particular integral??
\[y = \lambda + \mu x\]If
\[f(x) = p + qx + rx^2\]What is the particular integral??
\[y = \lambda + \mu x + v x^2\]If
\[y(x) = (x + 2)^2\]What is the form of the particular integral??
\[y = \lambda + \mu x + v x^2\]If
\[f(x) = pe^{kx}\]What is the particular integral??
\[y = \lambda e^{kx}\]If
\[f(x) = 10e^{-5x)\]What is the form of the particular integral??
\[y = \lambda e^{-5x}\]If
\[f(x) = p\cos(\omega x) + q\sin(\omega x)\]What is the particular integral??
\[y = \lambda \cos (\omega x) + \mu \sin (\omega x)\]If
\[f(x) = 10\cos\left(\frac{1}{2}x\right)\]What is the form of the particular integral??
\[y = \lambda \cos\left(\frac{1}{2}x\right) + \mu \sin\left(\frac{1}{2}x\right)\]For the differential equation
\[\frac{d^2y}{dx^2} - 5\frac{dy}{dx} + 6y = e^{2x}\]The complementary function has been found to be
\[Ae^{2x} + Be^{2x}\]What should use instead of $\lambda e^{2x}$??
\[y = \lambda x e^{2x}\]\[x^2 e^y \frac{dy}{dx} + 2x e^y = x\]
How could you rewrite this?
\[\frac{d}{dx}\left( y^2 \right)\]
What’s this equal to?
2021-09-10
What do you ignore when working out the integrating factor?
The constant of integration, $c$.
2022-01-11
\[e^{\int 2 dx} = e^{2x + c} = Ae^{2x}\]
What’s gone wrong working of the integrating factor here?
$c$ has been accounted for but it shouldn’t have been.
2022-01-19
Given
\[y = e^{px}(A\cos(kx) + B\sin(kx))\]what is the formula for $\frac{\text{d}y}{\text{d}x}$??
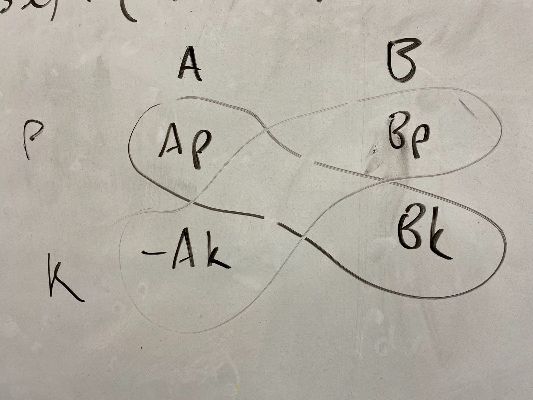
\[\frac{\text{d}y}{\text{d}x} = e^{px}((Ap + Bk)\cos(kx) + (Bp-Ak)\sin(kx))\]Given
\[y = e^{px}(A\cos(kx) + B\sin(kx))\]what is the nice “grid” for remembering the coefficients of the derivative for $\cos$ and $\sin$??
What would the format of the particular integral be for
\[\frac{\text{d}^2y}{\text{d}t^2} + 2 \frac{\text{d}y}{\text{d}t} + y = e^{-t} + 1\]if the complementary function is
\[y = (At + B)e^{-t}\]??
\[y = \lambda t^2 e^{-t} + \mu\]What does a second-order homogenous differential equation look like?
2022-05-15
Why do you need two arbitrary constants for the general solution of second-order homogenous differential equations?
Since differentiating twice can remove constant terms and $x$ terms.