Artificial Intelligence MT24, Partial order planning
Flashcards
@Define a partial order plan, and explain why it is useful compared to a total order plan.
A partial order plan consists of:
- A set of actions
- A special $\text{Start}$ action which has the initial state as its effect
- A special $\text{Finish}$ action which has the goal description as its precondition
- Ordering constraints $A \prec B$
- Means action $A$ must be performed before action $B$
- Causal links $A \stackrel{p}\longrightarrow B$
- Means action $A$ achieves precondition $p$ of action $B$
Useful because:
- It plainly splits a plan up into its independent subproblems.
- The search space is smaller since there are many equivalent total order plans.
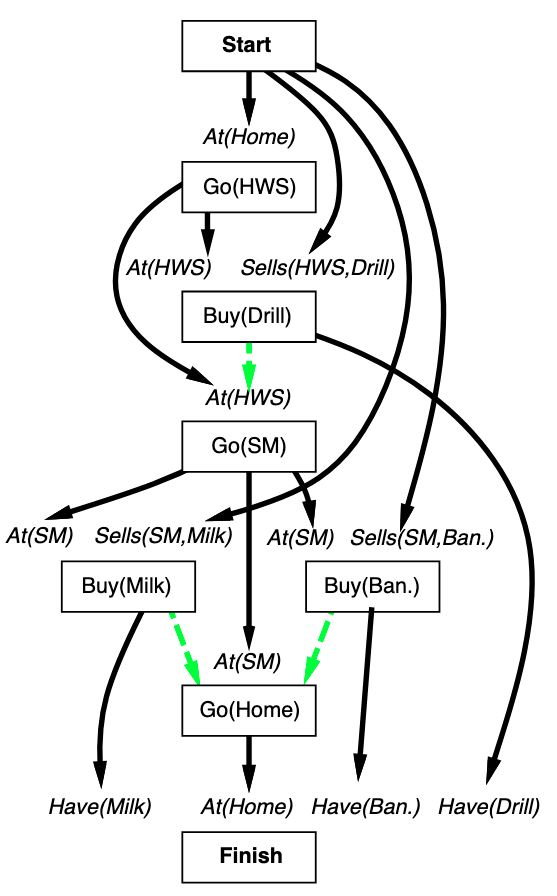
What do the black and green arrows mean in this diagram?

- Black arrows are causal links $A \stackrel{p}\longrightarrow B$, denoting that $A$ achieves precondition $p$ of action $B$. For example, the bottom left black arrow means that $\text{Buy}(\text{Milk})$ achieves precondition $\text{Have}(\text{Milk})$ of $\text{Finish}$.
- Green arrows represent ordering constraints. The bottom left green arrow means that $\text{Buy}(\text{Milk})$ has to occur before $\text{Go}(\text{Home})$.
A partial order plan consists of:
- A set of actions
- A special $\text{Start}$ action which has the initial state as its effect
- A special $\text{Finish}$ action which has the goal description as its precondition
- Ordering constraints $A \prec B$
- Means action $A$ must be performed before action $B$
- Causal links $A \stackrel{p}\longrightarrow B$
- Means action $A$ achieves precondition $p$ of action $B$
@Define what is meant by an “open precondition” when constructing such a plan?
- Means action $A$ must be performed before action $B$
- Means action $A$ achieves precondition $p$ of action $B$
A precondition $p$ of an action is open if it has no incoming causal link.
A partial order plan consists of:
- A set of actions
- A special $\text{Start}$ action which has the initial state as its effect
- A special $\text{Finish}$ action which has the goal description as its precondition
- Ordering constraints $A \prec B$
- Means action $A$ must be performed before action $B$
- Causal links $A \stackrel{p}\longrightarrow B$
- Means action $A$ achieves precondition $p$ of action $B$
Describe (briefly) the @algorithm used for constructing partial order plans.
- Means action $A$ must be performed before action $B$
- Means action $A$ achieves precondition $p$ of action $B$
- Begin with the start postconditions and the finish preconditions as in standard regression planning
- Add a causal link to achieve an open condition
- Add an order to prevent possible conflicts
- Backtrack if necessary
A partial order plan consists of:
- A set of actions
- A special $\text{Start}$ action which has the initial state as its effect
- A special $\text{Finish}$ action which has the goal description as its precondition
- Ordering constraints $A \prec B$
- Means action $A$ must be performed before action $B$
- Causal links $A \stackrel{p}\longrightarrow B$
- Means action $A$ achieves precondition $p$ of action $B$
@Define what it means for an action $C$ to conflict with $A \stackrel{p}\longrightarrow B$.
- Means action $A$ must be performed before action $B$
- Means action $A$ achieves precondition $p$ of action $B$
$C$ has effect $\lnot p$ and it could come after $A$ and before $B$ according to the current ordering.
Construct the last few steps of a partial order plan for the Sussman anomaly problem:
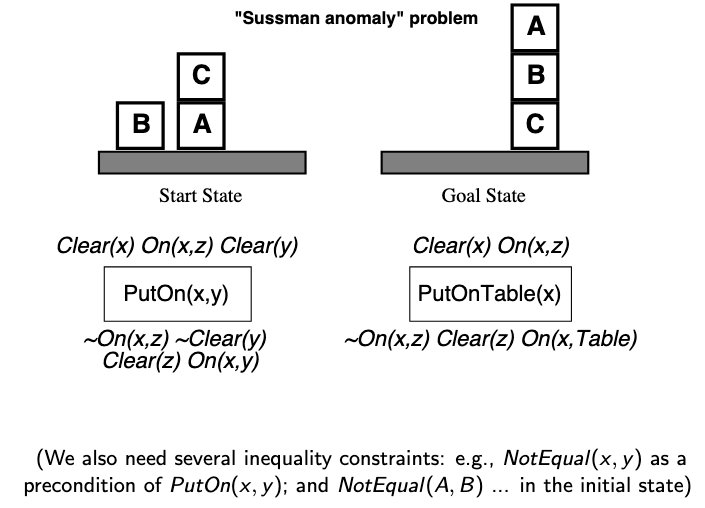
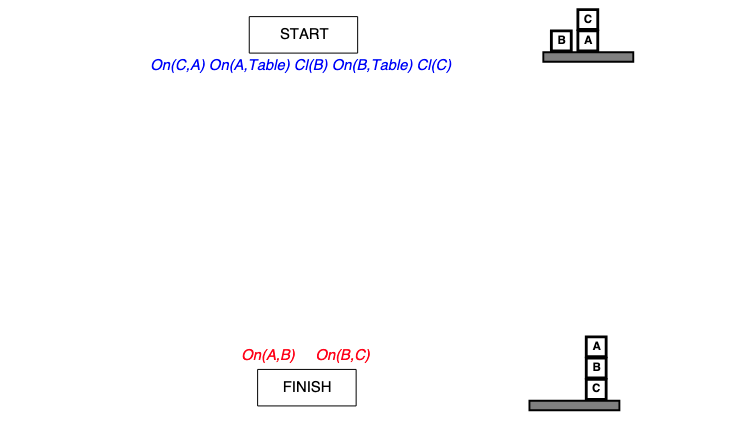
Your plan should achieve the goal conditions but might have unfulfilled preconditions.


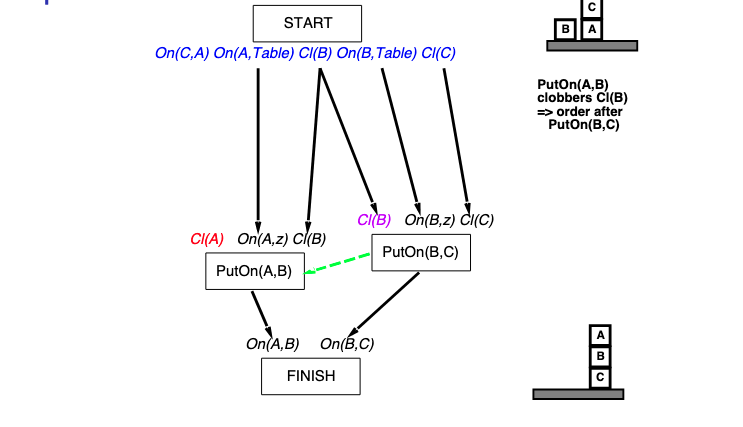
@example~