Artificial Intelligence MT24, Planning
Flashcards
STRIPS
What is the STRIPS language?
A logical language for encoding planning problems.
@Define the components of a planning problem when formulated in the STRIPS language.
- Predicates: A set of possible predicates (relations) used in formulating the problem.
- Constants: A set of constants (objects) used in formulating the problem.
- States: A set of positive ground atoms describing what holds currently, in terms of these predicates and constants
- e.g. $\{\text{At}(\textit{Home}), \text{Have}(\textit{Milk})\}$
- Initial state
- Goal: A set of ground atoms to be made true (also allowed a superset):
- e.g. $\{\text{At}(\textit{Home}), \text{Have}(\textit{Drill})\}$.
- Action: A precondition and postcondition
- Precondition: What must be true before an action is carried out
- Postcondition: A set of atoms to be added (appear positively) and a set of atoms to be removed (appear negatively)
Give an @example STRIPS action which describes buying a drill from a hardware store.
- Action: $\text{Buy}(\textit{Drill})$
- Precondition: $\text{At}(\textit{HardwareStore})$, $\text{Sells}(\textit{HardwareStore, Drill})$.
- Postcondition: $\lnot \text{Sells}(\textit{HardwareStore, Drill})$, $\text{Have}(\textit{Drill})$
In STRIPS, it is possible to define actions in terms of variables like so:
- Action: $\text{Buy}(\textit{x})$
- Precondition: $\text{At}(\textit{p})$, $\text{Sells}(\textit{x, p})$.
- Postcondition: $\lnot \text{Sells}(\textit{p, x})$, $\text{Have}(\textit{x})$
(note that $p$ doesn’t have to occur in the name of the action despite being in the preconditions and postconditions, instead this just creates actions that range over all possible values of $x$ and $p$)
What is the problem with this as it stands, and how can you overcome this problem?
$x$ might not be an object and $p$ might not be a place. In order to fix this, you need to add new atoms which effectively “type” the variables:
- Action: $\text{Buy}(\textit{x})$
- Precondition: $\text{At}(\textit{p})$, $\text{Sells}(\textit{x, p})$, $\text{IsPlace}(p)$, $\text{IsObject}(x)$.
- Postcondition: $\lnot \text{Sells}(\textit{p, x})$, $\text{Have}(\textit{x})$
What is the difference between PDDL and STRIPS?
STRIPS does not allow negative literals in preconditions of actions, whereas PDDL does.
Algorithms for planning
Describe the basics of the backward (regression) planning @algorithm.
(note this is distinct from partial order planning).
- Start with a goal state $G$
- Pick an action $A$ that is:
- Relevant: achieves literal in $G$, so contains a literal $B$ such that $B$ is in $G$
- Consistent: doesn’t undo a literal in $G$, so the postcondition doesn’t contain a literal $\lnot B$ such that $B$ is in $G$
- For simplicity, consider actions where variables occuring in the postcondition of the action also occur in the precondition (otherwise searching gets complicated)
- Compute the predecessor state
- Use $A^\ast$ to do this repeatedly until the initial state is reached
What are the advantages and disadvantages of forward, backward (regression) and partial order planning algorithms?
- Forward planning:
- Disadvantage: Many actions can be applicable to a state, so the branching factor is very high.
- Advantage: Each state is described fully as a set of ground atoms (there are no variables that need filling).
- Backward planning:
- Disadvantage: Partial state descriptions may contain atoms still in terms of variables.
- Advantage: It has a lower branching factor and is more goal-oriented (“the fan-in factor is usually lower than the fan-out factor”)
- Partial order planning:
- Disadvantage: More complex searching process (?)
- Advantage: It can decompose a planning problem into independent subproblems, each of which can be solved independently.
If a problem being solved by a planning algorithm is very simple, what can you often show about the backward planning algorithm?
It finds the solution within a polynomial number of steps.
Heuristics for planning
What are 4 main heuristics that can be used when using $A^\ast$ and STRIPS?
- Ignore preconditions
- Every action becomes applicable in every state
- Ignore negative effects
- No action can remove an atom from the current state
- State abstraction
- Remove all atoms over some predicate in pre- and post-conditions
- Subgoal independence
- Split all goal atoms into disjoint subsets, and consider min-cost plans to solve the subsets
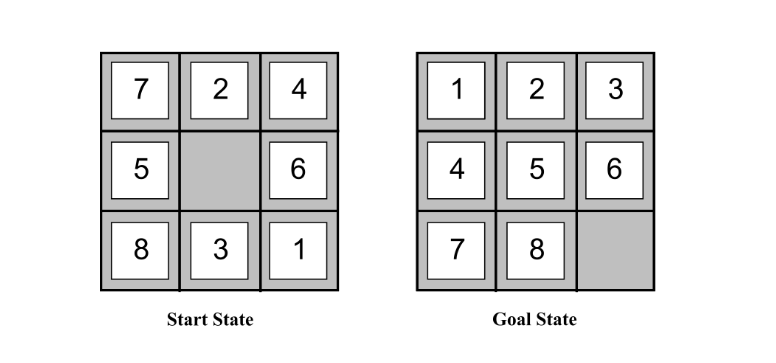
Consider the STRIPS formulation of the action of sliding tile $t$ from position $a$ to position $b$:
- Action: $\text{Slide}(t, a, b)$
- Precondition: $\text{Tile}(t)$, $\text{On}(t, a)$, $\text{Adjacent}(a, b)$, $\text{Empty}(b)$
- Effect: $\text{On}(t, b)$, $\text{Empty}(a)$, $\lnot \text{On}(t, a)$, $\lnot \text{Empty}(b)$
When solving planning problems like this with $A^\ast$, it’s useful to have a good heuristic. One general purpose planning heuristic is ignoring preconditions. Can you explain this, give the “updated” action definition, and describe the intuitive 8 puzzle-specific heuristic this leads to?

Remove all preconditions so that every action in available in every state. This leads to the new action:
- Action: $\text{Slide}(t, a, b)$
- Precondition: …
- Effect: $\text{On}(t, b)$, $\text{Empty}(a)$, $\lnot \text{On}(t, a)$, $\lnot \text{Empty}(b)$
and an optimal solution to this planning problem corresponds to the “number of tiles out of place” heuristic.
(also, this relaxed problem is at least as hard as the $\mathbf{NP}$-hard $\mathbf{SetCover}$ problem, since you’re picking the least number of actions to cover all atoms in the goal, but this could be seen as a good thing as $\mathbf{SetCover}$ has efficient approximation algorithms).

Consider the STRIPS formulation of the action of sliding tile $t$ from position $a$ to position $b$:
- Action: $\text{Slide}(t, a, b)$
- Precondition: $\text{Tile}(t)$, $\text{On}(t, a)$, $\text{Adjacent}(a, b)$, $\text{Empty}(b)$
- Effect: $\text{On}(t, b)$, $\text{Empty}(a)$, $\lnot \text{On}(t, a)$, $\lnot \text{Empty}(b)$
When solving planning problems like this with $A^\ast$, it’s useful to have a good heuristic. One general purpose planning heuristic is ignoring negative effects. Can you explain this and give the “updated” action definition?

Remove all negative atoms from the effect/postcondition. This leads to:
- Action: $\text{Slide}(t, a, b)$
- Precondition: $\text{Tile}(t)$, $\text{On}(t, a)$, $\text{Adjacent}(a, b)$, $\text{Empty}(b)$
- Effect: $\text{On}(t, b)$, $\text{Empty}(a)$

Consider the STRIPS formulation of the action of sliding tile $t$ from position $a$ to position $b$:
- Action: $\text{Slide}(t, a, b)$
- Precondition: $\text{Tile}(t)$, $\text{On}(t, a)$, $\text{Adjacent}(a, b)$, $\text{Empty}(b)$
- Effect: $\text{On}(t, b)$, $\text{Empty}(a)$, $\lnot \text{On}(t, a)$, $\lnot \text{Empty}(b)$
When solving planning problems like this with $A^\ast$, it’s useful to have a good heuristic. One general purpose planning heuristic is state abstraction. Can you explain this, give the “updated” action definition when considering the $\text{Empty}$ predicate, and explain the intuitive 8-puzzle heuristic this leads to?

Drop all atoms over some predicate. In the case of the $\text{Empty}$ predicate, this is
- Action: $\text{Slide}(t, a, b)$
- Precondition: $\text{Tile}(t)$, $\text{On}(t, a)$, $\text{Adjacent}(a, b)$
- Effect: $\text{On}(t, b)$, $\lnot \text{On}(t, a)$
The optimal solution to this relaxed problem corresponds to the Manhattan distance heuristic.

Consider the STRIPS formulation of the 8 puzzle.
When solving planning problems like this with $A^\ast$, it’s useful to have a good heuristic. One general purpose planning heuristic is subgoal independence. Can you explain this in detail?

- Let $G _ 1, \ldots, G _ n$ be disjoint subsets of goal atoms.
- Let $P _ 1, \ldots, P _ n$ be min-cost plans that achieve $G _ 1, \ldots, G _ n$
Then take as heuristic
\[\max_i \text{Cost}(P_i)\]
Consider the STRIPS formulation of the 8 puzzle.
When solving planning problems like this with $A^\ast$, it’s useful to have a good heuristic. One general purpose planning heuristic is subgoal independence. This involves considering:
- Let $G _ 1, \ldots, G _ n$ be disjoint subsets of goal atoms.
- Let $P _ 1, \ldots, P _ n$ be min-cost plans that achieve $G _ 1, \ldots, G _ n$
and then taking as a heuristic
\[\max_i \text{Cost}(P_i)\]
Sometimes it’s possible to do better than this using independent subproblems. Can you describe this?

Instead take as heuristic
\[\sum^n_{i = 1} \text{Cost}(P_i)\]This is possible when the plans $P _ i$ and $P _ j$ are independent, i.e. the effects of actions in $P _ i$ leave the preconditions and effects of all actions in $P _ j$ unchanged.