Computer Security MT24, Block modes

Created: January 10, 2025 | Updated: May 28, 2025 | About these notes | View in context | Study these flashcards

Flashcards

ECB, Electronic codebook

Suppose you have a cipher with encryption and decryption functions

\[\begin{aligned} &E : \mathcal K \times \mathcal M \to \mathcal C \\\\ &D : \mathcal K \times \mathcal C \to \mathcal M \end{aligned}\]

but want to encrypt a message longer than a single plaintext by splitting the message into several blocks.

@Define the electronic codebook (ECB) technique in this case.

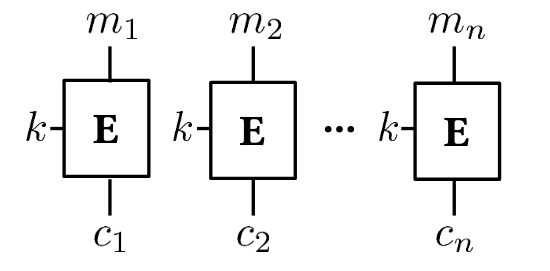
Each block $m _ i$ is encrypted separately with the same key:

\[c _ i = E _ k(m _ i)\]

Leads to weaknesses if plaintexts might include repeated or similar blocks.

Suppose you have a cipher with encryption and decryption functions

\[\begin{aligned} &E : \mathcal K \times \mathcal M \to \mathcal C \\\\ &D : \mathcal K \times \mathcal C \to \mathcal M \end{aligned}\]

but want to encrypt a message longer than a single plaintext by splitting the message into several blocks.

In this case, the electronic codebook (ECB) technique is to encrypt each block $m _ i$ separately with same key:

\[c _ i = E _ k(m _ i)\]

What are three problems with this approach?
  1. Repeated blocks encrypt to equal ciphertexts
  2. The enemy can reorder the message blocks
  3. Altering one ciphertext block affects only one plaintext block

CBC, Cipherblock chaining

Suppose you have a cipher with encryption and decryption functions

\[\begin{aligned} &E : \mathcal K \times \mathcal M \to \mathcal C \\\\ &D : \mathcal K \times \mathcal C \to \mathcal M \end{aligned}\]

but want to encrypt a message longer than a single plaintext by splitting the message into several blocks.

@Define the cipherblock chaining (CBC) technique in this case, by:

  • Defining $c _ i$ in terms of $m _ i$,
  • Defining $m _ i$ in terms of $c _ i$, and
  • Giving a recursive definition for $E^\ast _ k\langle m _ 1, \ldots, m _ k \rangle$.

.

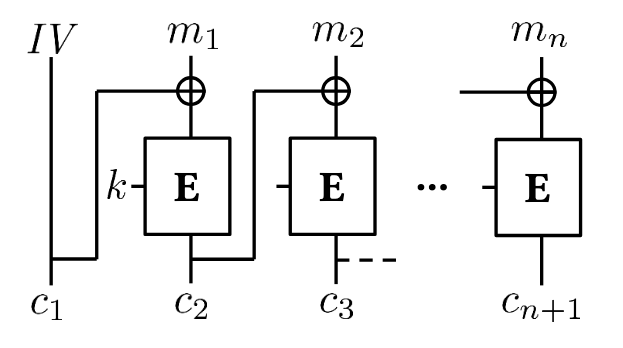
Encryption of block $i$ is XOR-ed with the plaintext of block $i+1$ before encryption, starting with an initialisation vector $IV$.

\[\begin{aligned} c _ 1 &= IV \\\\ c _ {i+1} &= E _ k(m _ i \oplus c _ i) \end{aligned}\] \[m_i = c_i \oplus D_k(c_{i+1})\] \[\begin{aligned} E^\ast_k\langle\rangle &= IV \\\\ E^\ast_k\langle m_1, \ldots, m_n \rangle &= E^\ast_k\langle m_1, \ldots, m_{n-1} \rangle \parallel \langle E_k(m_n \oplus \text{last}(E^\ast_k\langle m_1, \ldots, m_{n-1})) \rangle \end{aligned}\]

($IV$ must also be transmitted).

Which integrity properties does CBC introduce, and which integrity property is missing? How can you ensure this missing integrity property is recovered?

:

  • You can’t arbitrarily re-order, introduce or remove blocks.
  • You can truncate the message; this could be solved by also sending the hash of the message.
  • You can splice two streams together with only one corrupted block.

@exam~

Why must the IV in CBC be randomised?

Otherwise:

  • An attacker can tell if the same message (or same message prefix) was sent twice
  • If the attacker can introduce his own plaintext, then there is the potential for a blockwise adaptive chosen plaintext attack

OFB, Output feedback mode

Suppose you have a cipher with encryption and decryption functions

\[\begin{aligned} &E : \mathcal K \times \mathcal M \to \mathcal C \\\\ &D : \mathcal K \times \mathcal C \to \mathcal M \end{aligned}\]

but want to encrypt a message longer than a single plaintext by splitting the message into several blocks.

@Define the output feedback mode (OFB) technique in this case, and highlight a way in which you need to be careful.

Use iterated encryption of a random initialisation vector $IV$ to generate a pseudorandom stream $\langle r _ 2, r _ 3, \ldots \rangle$. Use this pseudorandom stream as a Vernam cipher on each block:

\[\begin{aligned} c _ 1 = r _ 1 &= IV \\\\ r _ {i+1} &= E _ k(r _ i) \\\\ c _ {i+1} &= m _ i \oplus r _ {i+1} \end{aligned}\]

Need to be careful that the pseudorandom stream doesn’t get into a cycle.

CTR, Counter mode

Suppose you have a cipher with encryption and decryption functions

\[\begin{aligned} &E : \mathcal K \times \mathcal M \to \mathcal C \\\\ &D : \mathcal K \times \mathcal C \to \mathcal M \end{aligned}\]

but want to encrypt a message longer than a single plaintext by splitting the message into several blocks.

@Define the counter mode (CTR) technique in this case.

Use encryption of “shifts” of an initialisation vector $IV \oplus i$ to generate a pseudorandom stream $\langle r _ 2, r _ 3, \ldots \rangle$. Use this pseudorandom stream as a Vernam cipher on each block:

\[\begin{aligned} r _ i &= E _ k(IV \oplus i) \\\\ c _ 1 &= IV \\\\ c _ {i+1} &= m _ i \oplus r _ {i+1} \end{aligned}\]

Need to be careful that the pseudorandom stream doesn’t get into a cycle.

What are some of the advantages and disadvantages of CTR?
  • Advantage: Prevents trimming the start of a message.
  • Disadvantage: Local changes to ciphertext only affect one block.

GCM, Galois counter mode

Briefly describe the purpose of Galois counter mode.

A block mode, similar to CTR, which encrypts long messages and simultaneously uses the key of the underlying block cipher to produce a tag for message integrity.



Related posts