Lecture - Theories of Deep Learning MT25, IV, Data classes for which DNNs can overcome the curse of dimensionality and Attention modules
Visualise the figure in Hein (2020) describing the “hidden manifold model”.
@Define the hidden manifold model as in Hein (2020) for generating datasets.
where
- $F \in \mathbb R^{d, n}$ are the $d$ features used to represent the data
- $C \in \mathbb R^{p, d}$ combines the $d < n < p$ features
- $f$ is a nonlinear function
How does Pascanu (2014) make an argument for the expressivity of ReLU DNNs based on hyperplane arrangements?
Since ReLU is piecewise linear, the output of a ReLU DNN is a piecewise linear function. They show that the number of possible regions of the input where the function can take on a different linear function is at least
\[\prod^L _ {\ell = 0} n _ \ell^{\text{min}\{n _ 0, n _ \ell / 2\}}\]where the input is $\mathbb R^{n _ 0}$ and the hidden layers are of width $n _ 1, \ldots, n _ L$.
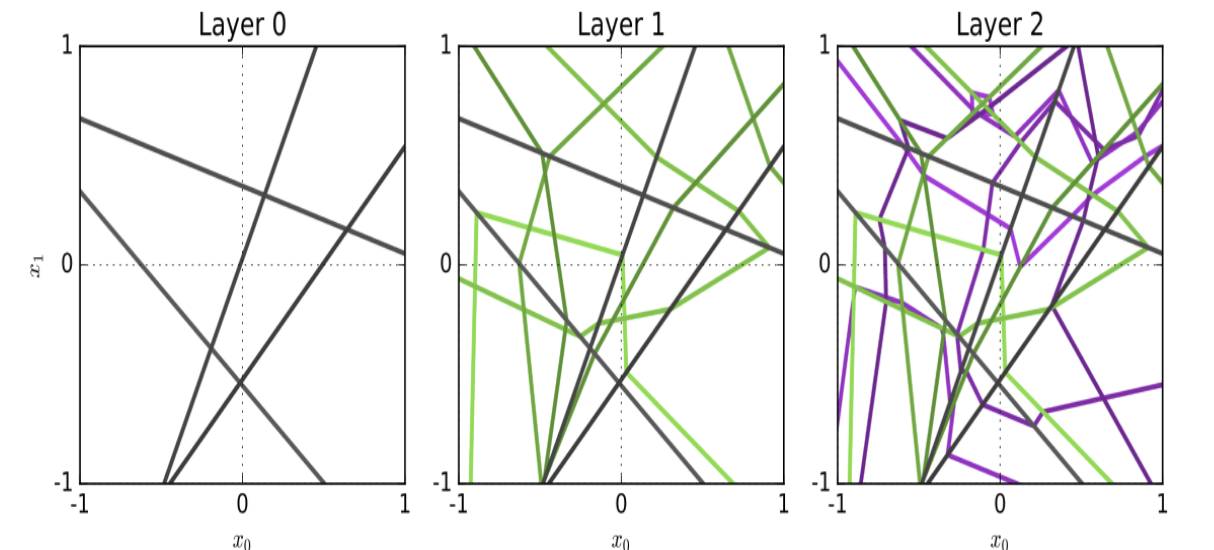
How does Raghu (2016) make an argument for the expressivity of DNNs based on trajectory lengths?
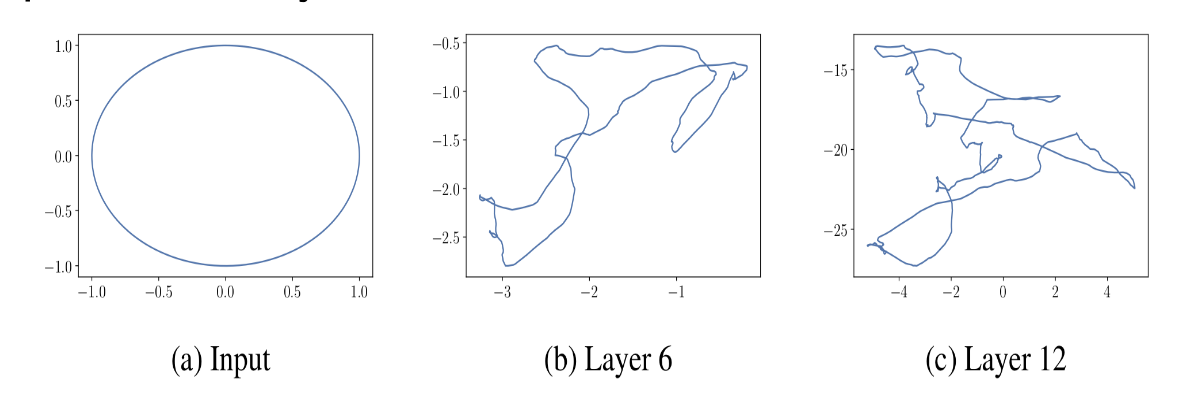
They show that a circle passed through a random DNN with an increasing number of layers can draw more and more complicated shapes, formalised as a growing arc length in expectation.
Other notes
- Often nets are unnecessarily wide (in terms of expressivity) because this makes them feasible to train
Papers mentioned
- [[Paper - Error bounds for approximations with deep ReLU networks, Yarotsky (2016)]]U
- [[Paper - When and when can deep networks avoid the curse of dimensionality, Poggio (2016)]]U Why and When Can Deep – but Not Shallow – Networks Avoid the Curse of Dimensionality: a Review
- Intrinsic Dimensionality Estimation of Submanifolds in $\mathbb R^d$
- Modeling the Influence of Data Structure on Learning in Neural Networks: The Hidden Manifold Model
- Deep Neural Network Approximation Theory
- On the number of response regions of deep feedforward networks with piecewise linear activations
- On the Expressive Power of Deep Neural Networks
- Trajectory growth lower bounds for random sparse deep ReLU networks
- Survey of Expressivity in Deep Neural Networks