MAT - Paper 2007 - Q1D
Flashcards
2021-10-14
Does the line $y = \frac{3}{4}x$ go through the circle
\[(x - 1)^2 + (y - 1)^2 = 1\]?? No way Jose.
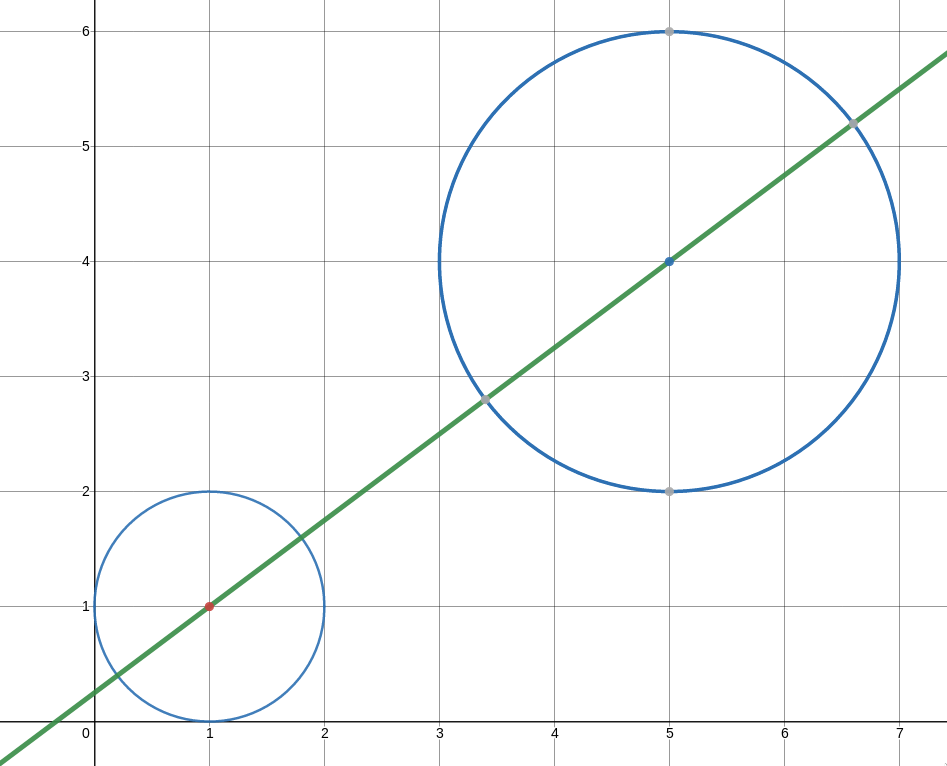
These are the circles
\[(x - 1)^2 + (y - 1)^2\]
and
\[(x - 5)^2 + (y - 4)^2 = 4\]What is the vector for moving from the little circle to the big circle??
\[\left(\begin{matrix} 4 \\\\ 3 \end{matrix}\right)\]
If the vector for moving between the centre of each of the two circles (Dad) is
\[\left(\begin{matrix} 4 \\\\ 3 \end{matrix}\right)\]
(magnitude $5$), then what fraction of the journey is taken up by moving out of the first circle and up to the outside of the second circle??
\[\frac{3}{5}\]When a coordinate geometry problem is getting tricky and you’re not allowed a calculator (i.e. the quadratic isn’t clearly factorisable or you’re having to substitute $y = \frac{3}{4}x + \frac{1}{4}$) then what could be an alternate way of tackling the problem?
Using vectors.