Computational Complexity HT25, Nondeterminism
-
[[Course - Computational Complexity HT25]]U
- [[Notes - Computational Complexity HT25, Time and space]]U
- [[Notes - Computational Complexity HT25, Mapping reductions]]U
- [[Notes - Computational Complexity HT25, Index of problems and reductions]]U
- [[Notes - Computational Complexity HT25, Turing reductions and oracles]]U
- See also:
- [[Notes - Models of Computation MT23, Turing machines]]U
- [[Notes - ADS HT24, NP-hardness and NP-completeness]]U
Flashcards
Basic definitions
When does a non-deterministic Turing machine accept an input, and when does it reject?
- Accept: There exists at least one accepting path
- Reject: All paths end with a reject state
@Define what it means for an NTM $M$ to run for time $t$.
For all $x \in \Sigma^\ast$, all paths of $M$ either accept or reject in time $t$.
@Define what it means for an NTM $M$ to run in space $s$.
For all $x \in \Sigma^\ast$, all paths of $M$ either accept or reject in space $s$.
Why is it not simply the case that
\[\mathsf{NTIME}(t) = \overline{\mathsf{NTIME}(t)}\]
by simply flipping the status of the deciding non-deterministic Turing machine?
To accept as a non-deterministic Turing machine means that there is at least one accepting path, and rejecting means that all paths end with a reject state. So flipping the output of one particular path does not tell you about the global properties.
@Prove that it’s accurate to characterise $\mathsf{NP}$ as the set of all languages $L$ such that there exists a polynomial time relation $R$ such that $\forall x$, $x \in L$ iff $\exists y$ such that $ \vert y \vert = \text{poly}( \vert x \vert )$ and $R(x, y) = 1$.
Suppose that some language $L$ satisfies the above condition where $M$ is a polynomial time decider for $R$. We wish to show it’s accepted by some polynomial time NTM $N$. Define as follows:
- $N$ on input $x$:
- Computes $p( \vert x \vert )$, guessing $y$ of length $\le p( \vert x \vert )$.
- Runs $M(x, y)$ and accepts iff $M$ accepts.
For the other direction, suppose that $N$ is a NTM running in time $q( \vert x \vert )$ and deciding a language $L$. Let $R(x, y) = 1$ iff $y = \langle c _ 1, c _ 2, \ldots, c _ t \rangle$ encodes an accepting computation of $M$ on $x$.
Note that each configuration $c _ i$ of $M$ has size $O(q( \vert x \vert ))$, and there are a maximum of $q( \vert x \vert )$ configurations visited when deciding $M(x)$, so the total size of $y$ is bounded by $q^2$, a polynomial.
Classes
@Define the class $\mathsf{NP}$.
@Define $\mathsf{NP}$ in terms of polynomially-sized witnesses.
$\mathsf{NP}$ is the set of all languages $L$ such that there exists a polynomial time relation $R$ such that $\forall x$, $x \in L$ iff $\exists y$ such that $ \vert y \vert = \text{poly}( \vert x \vert )$ and $R(x, y) = 1$.
@Define the class $\mathsf{NEXP}$.
@Define the class $\mathsf{coNP}$.
@Define co-$\mathsf{NP}$ in terms of polynomial-time relations.
$L \in \mathsf{coNP}$ iff there is a polynomial-time computable relation $R$ such that $x \in L$ iff $\forall y \in \{0, 1\}^{\text{poly}( \vert x \vert )} . R(x, y)$.
@Prove that $L \in \mathsf{coNP}$ iff there is a polynomial-time computable relation $R$ such that $x \in L$ iff $\forall y \in \{0, 1\}^{\le \text{poly}( \vert x \vert )} . R(x, y)$.
Suppose $L \in \mathsf{coNP}$. Then $\overline L \in \mathsf{NP}$. Therefore there is a polynomial time relation $\overline R$ such that $x \in \overline L$ iff $\exists y \in \{0, 1\}^{\text{poly}( \vert x \vert )} y . \overline R(x, y)$. Thus $x \in L$ iff $\forall y \in \{0, 1\}^{\text{poly}( \vert x \vert )} . \lnot \overline R$, which gives the required characterisation by taking $R := \lnot \overline R$.
Now suppose that $L$ is characterised by $x \in L$ iff $\forall y \in \{0, 1\}^{\text{poly}( \vert x \vert )} . R(x, y)$. Then $x \in \overline L$ iff $\exists y \in \{0, 1\}^{\text{poly}( \vert x \vert )} y . \lnot R(x, y)$, and so $\overline L$ is in $\mathsf{NP}$. Hence $L \in \mathsf{coNP}$.
Simulation arguments
Simulating deterministic time with non-deterministic time
Suppose $T : \mathbb N \to \mathbb N$ is a time bound. @State a simple relationship between $\mathsf{DTIME}(T)$ and $\mathsf{NTIME}(T)$.
Simulating non-deterministic time with deterministic space
Suppose $T : \mathbb N \to \mathbb N$ is a space-constructible time bound. @State a relationship between $\mathsf{NTIME}(T)$ and $\mathsf{DSPACE}(T)$.
Suppose $T : \mathbb N \to \mathbb N$ is a space-constructible time bound. @Prove that then
\[\mathsf{NTIME}(T) \subseteq \mathsf{DSPACE}(T)\]
Overall idea: Enumerate all possible sequences of configurations of the non-deterministic machine, and check if they are valid. This might take a very long time but only uses $O(T)$ space.
Suppose $L \in \mathsf{NTIME}(T)$ with corresponding TM $M$.
Define a deterministic TM $N$ which runs in space $O(T)$ as follows. Let $d$ be a constant that bounds the number of successors of any configuration of $M$.
On input $x$:
- $N$ uses the space constructibility of $T$ to compute $T( \vert x \vert )$.
- $N$ enumerates all strings of length $T( \vert x \vert )$ over the alphabet $\{1, 2, \ldots, d\}$ which represent possible computation paths of $M$.
- For each possible computation path, $N$ checks if the computation path is valid and leads to acceptance, halting and accepting if it does.
- If none of the computation paths is a valid accepting path, $N$ rejects.
Note that $N$ only uses space $O(T( \vert x \vert ))$ since at any point in its computation, it only needs to store the current computation path of $M$ being simulated, as well as the current configuration of $M$.
Since the computation path being simulates is of length $O(T( \vert x \vert ))$, $M$ uses space at most $O(T( \vert x \vert ))$, and hence the stored configuration of $M$ also has size at most $O(T( \vert x \vert ))$.
Simulating non-deterministic space with deterministic time
Suppose $S : \mathbb N \to \mathbb N$ is a space-constructible bound with $S(n) = \Omega(\log n)$. @State a result about $\mathsf{NSPACE}$ and $\mathsf{DTIME}$ in this context.
Suppose $S : \mathbb N \to \mathbb N$ is a space-constructible bound with $S(n) = \Omega(\log n)$. @Prove that then:
\[\mathsf{NSPACE}(S) \subseteq \mathsf{DTIME}(2^{O(S)})\]
Let $L$ be any language in $\mathsf{NSPACE}(S)$ and $M$ a Turing machine that decides $L$ in space $O(S)$.
Note that there are at most $(n+1)2^{O(S)}$ possible configurations of $M$ on any input of length $n$, since there are at most $(n+1)$ possible positions of the input tape head, at most $\text{poly}(S)$ positions of the work tape heads, at most $2^{O(S)}$ possible contents of the work tapes, and at most constantly many possible states of the machine.
Treat these configurations as a graph with edges between configurations. Implement BFS on the configuration graph, which takes space $2^{O(S)}$ by constructing the adjacency matrix.
Savitch’s theorem, simulating non-deterministic space with deterministic space
See [[Notes - Computational Complexity HT25, Savitch’s theorem]]U.
$\mathsf{NP}$-hardness and $\mathsf{NP}$-completeness
@Define what it means for a language $L \subseteq \{0, 1\}^\ast$ to be $\mathsf{NP}$-hard.
For all $L’ \in \mathsf{NP}$, $L’ \le _ m^\text{poly} L$.
@State and @justify a proposition which relates $\mathsf{NP}$-completeness of a language and the $\mathsf{P} \stackrel?= \mathsf{NP}$ question.
Suppose $L$ is $\mathsf{NP}$-complete. Then $\mathsf{P} \ne \mathsf{NP}$ iff $L \notin \mathsf{P}$. (i.e. to prove that $\mathsf{P} \ne \mathsf{ NP }$, it suffices to show that any $\mathsf{ NP}$-complete language is not in $\mathsf{P}$).
Proof: The forward direction follows from the fact that if $L \in \mathsf{ P}$, then all $\mathsf{NP}$-languages could be decided in polynomial time, and the backwards direction follows from the fact that $L \in \mathsf{NP}$.
@Define the bounded NTM acceptance problem, and @prove that it’s $\mathsf{NP}$-complete.
Proof: To establish that $L$ is $\mathsf{NP}$, run the universal NTM for $t$ steps with input $\langle M, x \rangle$ and accept only if $M$ accepts $x$. This uses polynomial time.
Now suppose $L’ \in \mathsf{NP}$ and $M _ {L’}$ is an NTM deciding $L$ in time $p( \vert x \vert )$ for large enough $x$. Define
\[f(x) = \langle M_{L'}, x, 1^{p(|x|)} \rangle\]Note that $M _ L$ is a fixed machine that does not depend on the input, and hence $f(x)$ can be computed in polynomial time. Then $x \in L \iff M _ L$ accepts $x$ within $p( \vert x \vert )$ steps, as required.
$\mathsf{NP}$-complete problems
See also: [[Notes - Computational Complexity HT25, Index of problems and reductions]]U.
@Prove that $\mathsf{CLIQUE}$ is $\mathsf{NP}$-complete.
Overall idea: Introduce a variable for each literal in each clause, and connect everything apart from literals to their duals and literals in the same clause. Then cliques of size the number of clauses must correspond to satisfying assignments.
We reduce from $3\text{-}\mathsf{SAT}$, i.e. given a formula 3CNF $\varphi$ we wish to find $\langle G, k \rangle$ such that $\varphi$ is satisfiable iff $\langle G, k \rangle \in \mathsf{CLIQUE}$.
Suppose $\varphi = \bigwedge _ {i = 1}^k (a _ i \lor b _ i \lor c _ i)$. For each literal $a _ i, b _ i, c _ i$ in $\varphi$, introduce a corresponding node of $G$ (and so there might be multiple occurrences of $x _ i$ in the graph). Add edges between every node, except:
- A literal and its dual (i.e. $x _ i$ and $\overline{x _ i}$)
- Literals occurring in the same clause.
and let $k$ equal the number of clauses of $\varphi$.
Now suppose $\varphi$ has a satisfying assignment. Then at least one node is true in every clause. Pick one of the true literals arbitrarily. The nodes selected form a $k$-clique, since there are $k$ nodes and every node is connected to the other because each pair of nodes does not meet either of the conditions above.
Now suppose that $G$ has a $k$-clique. Construct an assignment by taking one literal from each of the triples corresponding to each clause introduced in the graph, and setting it to true. It’s straightforward to verify that this is a satisfying assignment.
Example:
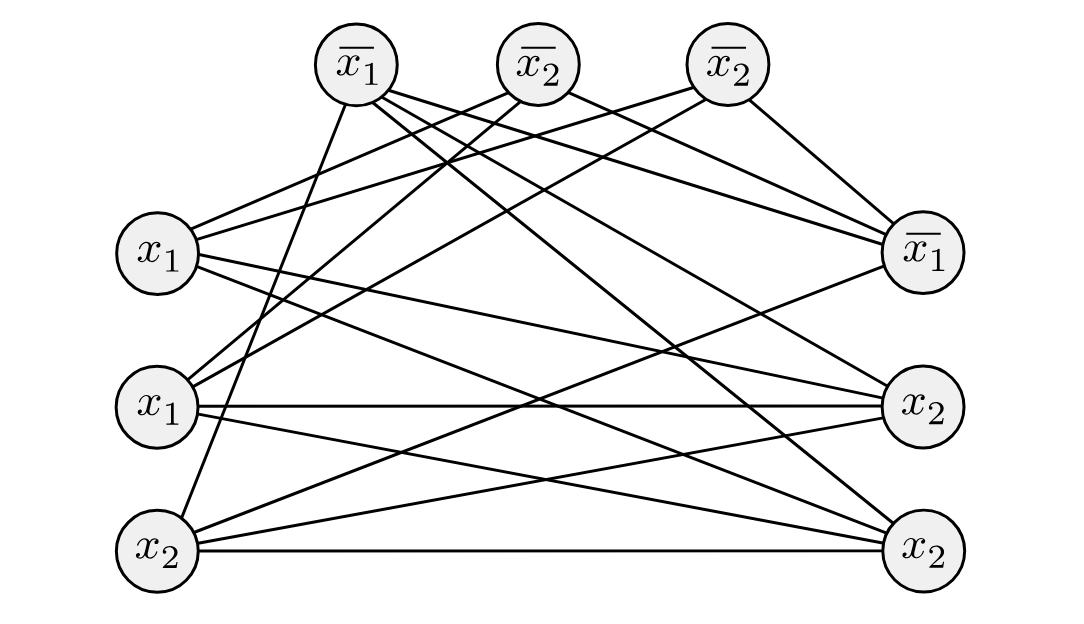
$\mathsf{coNP}$-complete problems
@Define what it means for a language $L$ to be $\mathsf{coNP}$-complete with respect to polynomial time $m$-reductions.
$L \in \mathsf{coNP}$ and for every language $L’ \in \mathsf{coNP}$, $L’ \le _ m^\text{poly} L$.
@State a relationship between $\mathsf{NP}$-complete languages and $\mathsf{coNP}$-complete languages.
$L$ is $\mathsf{coNP}$-complete with respect to polynomial time $m$-reductions iff $\overline L$ is $\mathsf{NP}$-complete with respect to polynomial time $m$-reductions.
@Define $\mathsf{TAUT}$ and @justify why it is $\mathsf{coNP}$-complete.
It is $\mathsf{coNP}$-complete as $\varphi$ is a tautology iff $\lnot \varphi$ is unsatisfiable, so $\mathsf{TAUT}$ and $\mathsf{UNSAT}$ polynomial-time $m$-reduce to one another. As $\mathsf{UNSAT}$ is $\mathsf{coNP}$-complete (it is the complement of a $\mathsf{NP}$-complete language), it follows that $\mathsf{TAUT}$ is $\mathsf{coNP}$-complete.
What is meant by the fact that “$\mathsf{NP}$ and $\mathsf{coNP}$ are equivalent with respect to polynomial-time computability”?
Any language $L \in \mathsf{NP}$ is decidable in polynomial time with oracle access to $\overline L \in \mathsf{coNP}$.
Search to decision reductions
@Prove that if $\mathsf P = \mathsf{NP}$, then there is a polynomial time algorithm which given a formula $\varphi$ outputs a satisfying assignment if $\varphi$ is satisfiable.
Let $A$ be a polynomial time algorithm for $\mathsf{SAT}$. We define a recursive algorithm $S$ which solves the search problem in polynomial time.
Given a formula $\varphi$, if $\varphi$ has no variables, $S$ evaluates $\varphi$ in polynomial time and outputs the empty string if $\varphi$ is true and “fail” otherwise.
If $\varphi$ does contain variables, let $x$ be the lexicographically first variable in $\varphi$. Let $\varphi _ 0$ be the formula obtained from $\varphi$ by substituting $x = 0$, and $\varphi _ 1$ be obtained by substituting $x = 1$. $S$ runs $A$ on $\varphi _ 0$ and if accepts, $S$ outputs $x = 0$ concatenated with $S(\varphi _ 0)$, otherwise $S$ outputs $x = 1$ concatenated with $S(\varphi _ 1)$.
This takes polynomial time, since there are polynomially many variables and each iteration takes polynomial time.
Suppose you have a decision oracle for checking the $k$-colorability of a graph. How could you actually find a $k$-colouring?
Iteratively try and connect pairs of vertices; if there remains a $k$-colouring even after they are connected then there is a $k$-colouring where they are set to the same colour.
@example~ @exam~
$\mathsf{NP}$-intermediate problems
Why does it unlikely that
\[\mathsf{FACTOR} = \lbrace \langle m, r \rangle \mid \exists s \text{ s.t. }1 < s < r \text{ and } s \mid m \rbrace\]
is $\mathsf{NP}$-complete (so called “$\mathsf{NP}$-intermediate”)?
This language is both in $\mathsf{NP}$ and $\mathsf{coNP}$ – a certificate is given by the factorisation of $m$. If this language were $\mathsf{NP}$-complete, it would imply that $\mathsf{NP} = \mathsf{coNP}$, which seems unlikely.