Computational Complexity HT25, Cook-Levin theorem
Flashcards
Basic statement
@State the Cook-Levin theorem.
$\mathsf{SAT}$ is $\mathsf{NP}$-complete.
Proof via tableaus
@Prove the Cook-Levin theorem, i.e. that $\mathsf{SAT}$ is $\mathsf{NP}$-complete.
$\mathsf{SAT}$ is $\mathsf{NP}$: A nondeterministic polynomial time machine can guess an assignment to the variables in a formula $\varphi$ and accept if the assignment satisfies $\varphi$.
$\mathsf{SAT}$ is $\mathsf{NP}$-hard: Fix some $\mathsf{NP}$ language $A$ with a corresponding NTM
\[N = (Q, \Sigma, \Gamma, \delta, q_0, q_\text{acc}, q_\text{rej})\]deciding $A$ in polynomial time. We may assume that $N$ runs in time $n^k$ for some constant $k$, and that it uses just a single tape (this is justified by the fact any $\ell$-tape NTM can be simulated by a single tape one).
A tableau for $N$ on input $w$ is an $n^k \times n^k$ table whose rows are the configurations of a particular branch of $N$ on input $w$.
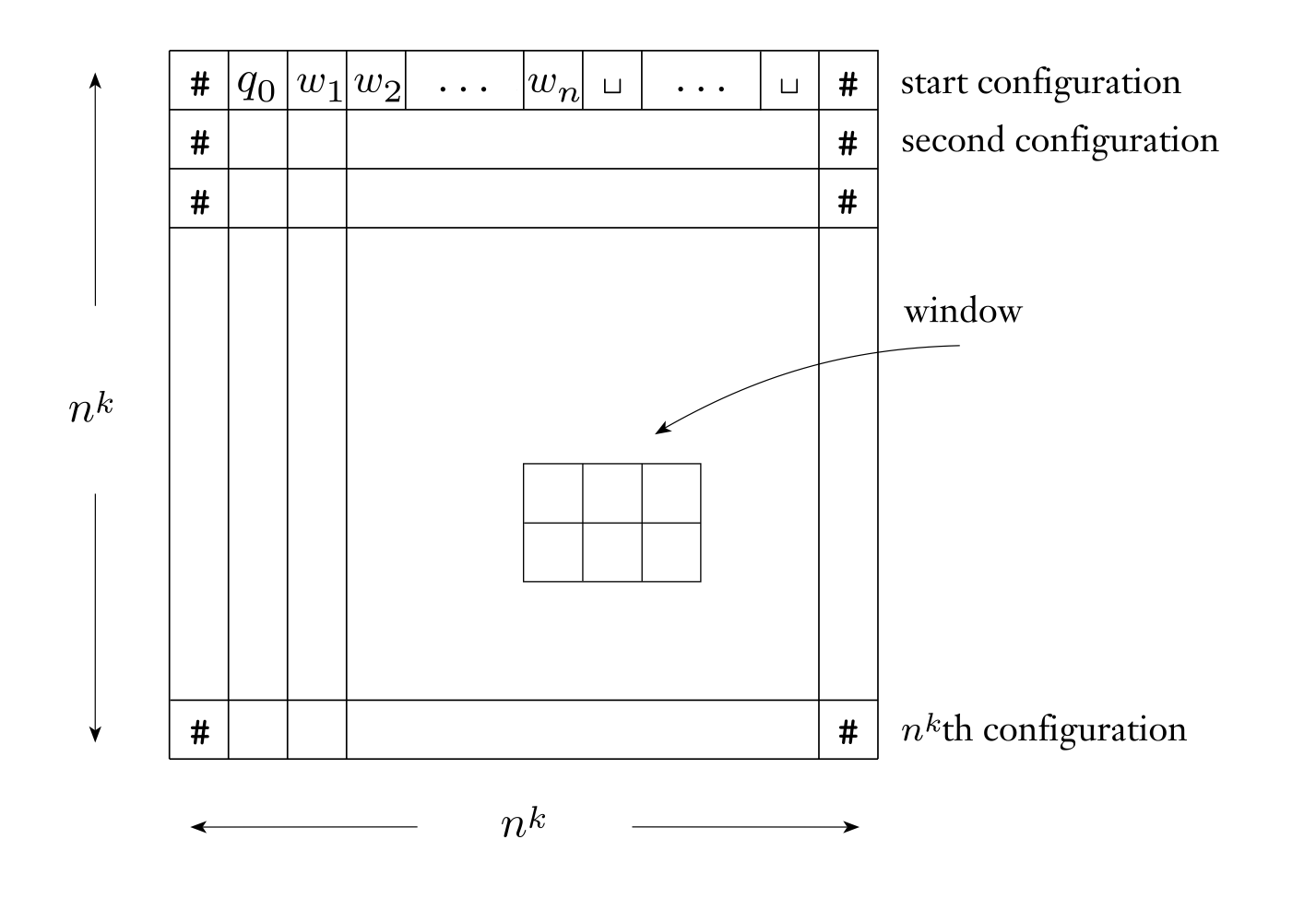
Each row corresponds to the contents of the tape in that configuration, along with the current state and the pointer. The location of the pointer is represented implicitly as being over the cell to the right of the current state symbol (so for example, if the row is $\mathcal Hw _ 1 w _ 2 q _ i w _ 3\mathcal H$, this represents that the tape’s contents are $w _ 1 w _ 2 w _ 3$ and the pointer is over $w _ 3$).
Say a tableau is accepting if any row of the tableau is an accepting configuration, so that every accepting tableau for $N$ on $w$ corresponds to an accepting computation branch of $N$ on $w$. So the problem of determining whether $N$ accepts $w$ is equivalent to the problem of determining whether an accepting tableau for $N$ on $w$ exists. We formulate this problem as determining the satisfiability of a CNF formula
\[\varphi = \varphi_\text{start} \land \varphi_\text{accept} \land \varphi_\text{cell} \land \varphi_\text{move}\]Variables of $\varphi$: Let $C = Q \cup \Gamma \cup \lbrace \mathcal H\rbrace$. The variables of $\varphi$ are $x _ {i, j, s}$ where $1 \le i, j \le n^k$, $s \in C$. Intuitively, we wish
\[x_{i, j, s} = 1 \iff \text{cell }(i, j) \text{ contains }s\]$\varphi _ \text{start}$ fixes the start of the tableau:
\[\varphi_\text{start} = x_{1, 1, \mathcal H} \land x_{1, 2, q_0} \land \cdots \land x_{1, n^k - 1, \sqcup}\land x_{1, n^k, \mathcal H}\]$\varphi _ \text{accept}$ ensures that an accepting configuration occurs:
\[\varphi_\text{accept} = \bigvee_{1 \le i, j \le n^k} x_{i, j, q_\text{acc} }\]$\varphi _ \text{cell}$ ensures that each cell is filled with exactly one symbol (possibly blank):
\[\varphi_\text{cell} = \bigwedge_{1 \le i, j \le n^k} \left[ \left( \bigvee_{s \in C} x_{i, j, s} \right) \land \left( \bigvee_{s, t \in C, s \ne t} (\overline{x_{i, j, s} } \lor \overline{x_{i, j, t} }) \right) \right]\]$\varphi _ \text{move}$ guarantees that each row of the configuration legally follows from the previous row: Call a $2 \times 3$ window of cells legal if that window does not violate the actions specified by $N$’s transition function.
\[\varphi_\text{move} = \bigwedge_{1 \le i < n^k, 1 < j < n^k} \varphi_\text{legal}(i, j)\]where
\[\varphi_{\text{legal}(i, j)} = \bigvee_{a_1, \ldots, a_6 \text{ is legal window} } x_{i, j-1, a_1} \land x_{i, j, a_2} \land x_{i, j+1, a_3} \land x_{i+1, j-1, a_4} \land x_{i+1, j, a_5} \land x_{i+1, j+1, a_6}\]We claim that if the top row of the tableau is the start configuration and every window in the tableau is legal, each row of the tableau is a configuration that follows from the preceding one.
Consider two adjacent configurations in the tableau, call these the upper configuration and the lower configuration. In the upper configuration, every cell that contains a tape symbol that isn’t adjacent to a state symbol is the centre top cell in a window whose top row contains no states. Therefore, that symbol must appear unchanged in the centre bottom of the window. Hence it appears in the same position in the bottom configuration.
The window containing the state symbol in the centre top cell guarantees that the corresponding three positions are updated consistently with the transition function. Therefore, if the upper configuration is a legal configuration, so is the lower configuration, and the lower one follows the upper one according to $N$’s rules. (@todo, illustration)
Note that all these formulas are polynomially sized, and that this formula can be constructed in polynomial time (one slight complication is that we need an extra logarithmic factor to index the variables, but this does not matter since we can consider a larger polynomial).
The formula is almost in CNF form, except for $\varphi _ \text{move}$, which is a conjunction of disjunctions of conjunctions. By the distributive laws for Boolean formulae, we may replace the disjunctions of conjunctions by conjunctions of disjunctions. This might lead to a blow-up in the size of the formula, but since the disjunction is over possible legal windows (which depends only on $ \vert M \vert $), each of which has size $6$, it follows that the size of the formula does not grow with $N$.
Hence $\mathsf{SAT}$ is $\mathsf{NP}$-complete.
The hard part of proving the Cook-Levin theorem is showing that $\mathsf{SAT}$ is $\mathsf{NP}$-hard. One proof does this by first fixing $\mathsf{NP}$ language $A$ with a corresponding NTM
\[N = (Q, \Sigma, \Gamma, \delta, q_0, q_\text{acc}, q_\text{rej})\]
deciding $A$ in time $n^k$, and we may assume it uses just a single tape. Then we consider a tableau for $N$ on input $w$, which is an $n^k \times n^k$ table whose rows are the configurations of a particular branch of $N$ on input $w$.

Each row corresponds to the contents of the tape in that configuration, along with the current state and the pointer. The location of the pointer is represented implicitly as being over the cell to the right of the current state symbol (so for example, if the row is $\mathcal Hw _ 1 w _ 2 q _ i w _ 3\mathcal H$, this represents that the tape’s contents are $w _ 1 w _ 2 w _ 3$ and the pointer is over $w _ 3$).
Say a tableau is accepting if any row of the tableau is an accepting configuration, so that every accepting tableau for $N$ on $w$ corresponds to an accepting computation branch of $N$ on $w$, and thus have reduced the problem of determining whether $N$ accepts $w$ to the problem of determining whether an accepting tableau for $N$ on $w$ exists.
Can you give a set of variables and @define a formula which is equivalent to the satisfiability problem of $N$ on $x$?

Variables of $\varphi$: Let $C = Q \cup \Gamma \cup \lbrace \mathcal H\rbrace$. The variables of $\varphi$ are $x _ {i, j, s}$ where $1 \le i, j \le n^k$, $s \in C$. Intuitively, we wish
\[x_{i, j, s} = 1 \iff \text{cell }(i, j) \text{ contains }s\]$\varphi _ \text{start}$ fixes the start of the tableau:
\[\varphi_\text{start} = x_{1, 1, \mathcal H} \land x_{1, 2, q_0} \land \cdots \land x_{1, n^k - 1, \sqcup}\land x_{1, n^k, \mathcal H}\]$\varphi _ \text{accept}$ ensures that an accepting configuration occurs:
\[\varphi_\text{accept} = \bigvee_{1 \le i, j \le n^k} x_{i, j, q_\text{acc} }\]$\varphi _ \text{cell}$ ensures that each cell is filled with exactly one symbol (possibly blank):
\[\varphi_\text{cell} = \bigwedge_{1 \le i, j \le n^k} \left[ \left( \bigvee_{s \in C} x_{i, j, s} \right) \land \left( \bigvee_{s, t \in C, s \ne t} (\overline{x_{i, j, s} } \lor \overline{x_{i, j, t} }) \right) \right]\]$\varphi _ \text{move}$ guarantees that each row of the configuration legally follows from the previous row: Call a $2 \times 3$ window of cells legal if that window does not violate the actions specified by $N$’s transition function.
\[\varphi_\text{move} = \bigwedge_{1 \le i < n^k, 1 < j < n^k} \varphi_\text{legal}(i, j)\]where
\[\varphi_{\text{legal}(i, j)} = \bigvee_{a_1, \ldots, a_6 \text{ is legal window} } x_{i, j-1, a_1} \land x_{i, j, a_2} \land x_{i, j+1, a_3} \land x_{i+1, j-1, a_4} \land x_{i+1, j, a_5} \land x_{i+1, j+1, a_6}\]Proof via $\mathsf P \subseteq \mathsf P _ {/\mathsf{poly} }$
@Define the $\mathsf{CircuitSAT}$ language.
@Prove that
\[\mathsf{CircuitSAT} = \lbrace c \in \lbrace 0,1\rbrace^\ast \mid c \text{ represents a boolean-valued circuit with satisfying assignment} \rbrace\]
is $\mathsf{NP}$-complete, relying on a big result about polynomial-size circuit families.
$\mathsf{CircuitSAT}$ is $\mathsf{NP}$: A satisfying assignment to the circuit can serve as a certificate.
$\mathsf{CircuitSAT}$ is $\mathsf{NP}$-hard: If $L \in \mathsf{NP}$, then there exists a polynomial time TM $M(x, y)$ such that $x \in L$ iff $M(x, u) = 1$ for some $u \in \lbrace 0, 1 \rbrace^{p( \vert x \vert )}$. But by the result that $\mathsf P = \mathsf P _ {/\mathsf{poly} }^\text{unif}$, it follows that there is a polynomial-time transformation from $M(x, \cdot)$ to a circuit $C$ such that $M(x, u) = C(u)$ for every $u$. Hence $x \in L$ iff $C \in \mathsf{CircuitSAT}$.
@Prove that $\mathsf{CircuitSAT} \le _ m^p \mathsf{3SAT}$ where
\[\mathsf{CircuitSAT} = \lbrace c \in \lbrace 0,1\rbrace^\ast \mid c \text{ represents a boolean-valued circuit with satisfying assignment} \rbrace\]
and then use this to justify the Cook-Levin theorem, i.e. that $\mathsf{SAT}$ is $\mathsf{NP}$-complete.
Initial reduction: Let $C$ be a circuit. We aim to find a 3CNF formula $\varphi$ such that $C$ and $\varphi$ agree.
For every node $v _ i$ of $C$, there is a corresponding variable $x _ i$ in $\varphi$.
Case $v _ i$ is a conjunction: Want to find a 3CNF formula equivalent to “$x _ i = (x _ j \land x _ k)$”. Add to $\varphi$ the clauses
\[(\overline{x_i} \lor \overline{x_j} \lor x_k) \land (\overline{x_i} \lor x_j \lor \overline{x_k}) \land (\overline{x_i} \lor x_j \lor x_k) \land (x_i \lor \overline{x_j} \lor \overline{x_k})\]Case $v _ i$ is a disjunction: Add to $\varphi$ the clauses expressing that “$x _ i = (x _ j \lor x _ k)$”.
Case $v _ i$ is a negation: Add to $\varphi$ the clauses expressing that “$x _ i = \lnot x _ j$”:
\[(x_i \lor x_j) \land (\overline{x_i} \lor \overline{x_j})\]Case $v _ i$ is output: Add to $\varphi$ the clause $(x _ i)$.
Then $\varphi$ is satisfiable iff $C$ is, and this reduction runs in polynomial time.
Cook-Levin theorem: We have that:
- $\mathsf{3SAT} \le _ m^p \mathsf{SAT}$, by a straightforward reduction
- $\mathsf{CircuitSAT} \le _ m^p \mathsf{3SAT}$ by the above
- So $\mathsf{CircuitSAT} \le^p _ m \mathsf{SAT}$ by transitivity
- $\mathsf{CircuitSAT}$ is $\mathsf{NP}$-complete by a result appealing to $\mathsf P \subseteq \mathsf P _ {/\mathsf{poly} }$ applied to the witness characterisation of $\mathsf{NP}$
- So $\mathsf{SAT}$ is $\mathsf{NP}$-complete.
Relativisation
The Cook-Levin theorem is a “non-relativising” result, i.e. it does not hold when the Turing machines under consideration are given access to an oracle: “Does the Cook-Levin theorem relativise?”.