Notes - Computational Complexity HT25, PSPACE-completeness

$L \in \mathsf{PSPACE}$ and for every $L’ \in \mathsf{PSPACE}$, $L’ \le _ m^\text{poly} L$.

If $L \in \mathsf P$, any language in $\mathsf{PSPACE}$ can be solved in polynomial time using the mapping reduction.

If $\mathsf{PSPACE} = \mathsf P$, then trivially $L \in \mathsf{PSPACE}$ implies $L \in \mathsf P$.

\[\mathsf{TQBF} = \\{\langle \varphi \rangle \mid \varphi \text{ is a true Boolean} \text{ sentence}\\}\]

i.e. a true “totally quantified boolean formula”.

The major result is that $\mathsf{TQBF}$ is $\mathsf{PSPACE}$-complete.

$\mathsf{TQBF}$ is in $\mathsf{PSPACE}$: Consider the Turing machine $M$ which implements the following procedure:

• $M(\langle \varphi \rangle)$:
  • If $\varphi$ contains no quantifiers, then it is an expression with only constants, so evaluate $\varphi$ and accept iff it is true.
  • If $\varphi = \exists x . \psi$ for some $\psi$, recursively call $M$ on $\psi[0 / x]$ and $\psi[1/x]$, and accept iff either runs accept.
  • If $\varphi = \forall x . \psi$ for some $\psi$, recursively call $M$ on $\psi[0 / x]$ and $\psi[1/x]$, and accept iff both runs accept.

$M$ decides $\mathsf{TQBF}$, and observe that the depth of the recursion is at most the number of variables. At each level, it suffices to store the value of one variable, so the space used is $O(m)$, where $m$ is the number of variables that appear in $\varphi$.

Therefore $T$ runs in linear space.

---

$\mathsf{TQBF}$ is $\mathsf{PSPACE}$-hard: Consider an arbitrary language $A \in \mathsf{PSPACE}$ with corresponding deterministic TM $N$ deciding $A$ in space $n^k$ for some $k$, we may also assume that $N$ uses a single tape. We show that it’s possible to construct sentences

\[\varphi_{c_1, c_2, t}\]

which are true iff $N$ can go from $c _ 1$ to $c _ 2$ in at most $t$ steps. The result then follows from considering the polynomial time function which takes some $w$ as a potential input to $M$ and constructs the polynomially-sized sentence

\[\varphi_{c_\text{start}, c_\text{accept}, 2^{dn^k} }\]

where $d$ is a constant such that $N$ has at most $2^{dn^k}$ possible configurations on an input of length $n$. Then giving this sentence to a decider for $\mathsf{TQBF}$ determines whether $N$ accepts $w$.

Details for how a tableau can be represented are at the end of this flashcard.

If $t = 1$, then we can construct $\varphi _ {c _ 1, c _ 2, t}$ as saying that either $c _ 1$ equals $c _ 2$ or $c _ 2$ follows from $c _ 1$ in a single step of $M$. Equality can be represented straightforwardly. To express that $c _ 1$ yields $c _ 2$ in a single step of $N$, we can write boolean expressions stating that each triple of $c _ 1$’s cells correctly yields the content of the corresponding triple of $c _ 2$’s cells.

If $t > 1$, we construct $\varphi _ {c _ 1, c _ 2, t}$ as follows:

\[\varphi_{c_1, c_2, t} = \exists m_1 \forall (c_3, c_4) \in \\{(c_1, m_1), (m_1, c_2)\\} \left[ \varphi_{c_3, c_4, t/2} \right]\]

This is a compact representation of the equivalent formula:

\[\varphi_{c_1, c_2, t}' = \exists m_1 \left[\varphi_{c_1, m_2, t/2} \land \varphi_{m_1, c_2, t/2}\right]\]

(this is the Fisher-Rabin trick, where the conjunction of two formulas is replaced by a universal quantifier, also used in [[Notes - Logic and Proof MT24, Lower bounds for deciding real arithmetic]]^U).

Here $m _ 1$ represents a configuration of $M$, and $\exists m _ 1$ is really shorthand for $\exists x _ 1 \exists x _ 2 \cdots \exists x _ l$ where $l = O(n^k)$ and $x _ 1, \ldots, x _ l$ are the variables that encode $m _ 1$.

To see that the formula $\varphi _ {c _ \text{start}, c _ \text{accept}, 2^{ds(n)}}$ is polynomially sized, note that each level of the recursion adds a portion of the formula that is linear in the size of the configurations and thus is of size $O(n^k)$. Since the number of levels of the recursion is $\log(2^{dn^k})$, this means the total size of the formula is $O(n^{2k})$.

---

Details for tableau representations:

A tableau for $N$ on input $w$ is an $n^k \times 2^{dn^k}$ table whose rows are the configurations of a particular branch of $N$ on input $w$ (note that this is slightly different from the proof of Savitch’s theorem, where the tableau has size $n^k \times n^k$, but by using the trick above we don’t need to explicitly encode every cell using a unique variable).

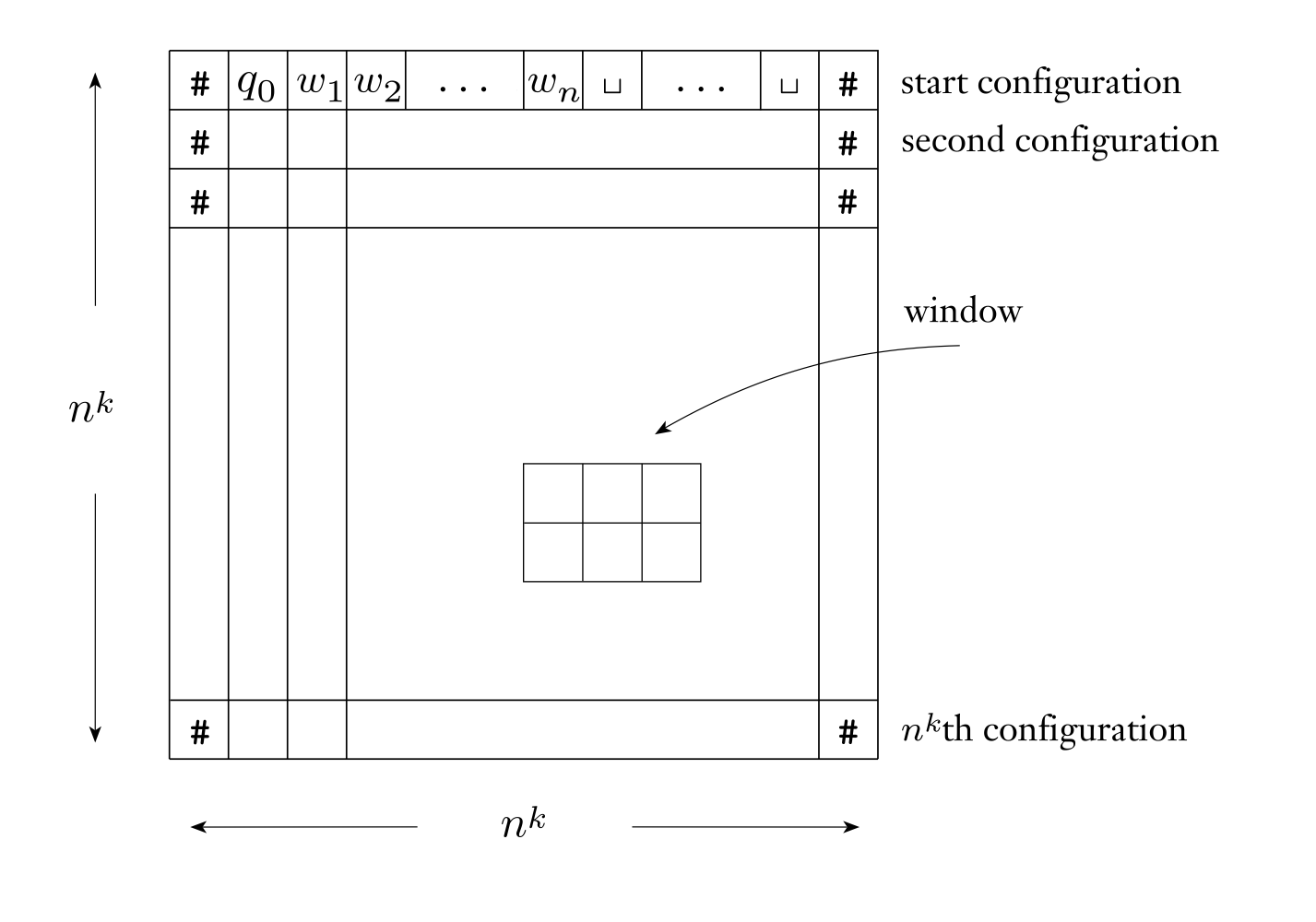
Each row corresponds to the contents of the tape in that configuration, along with the current state and the pointer. The location of the pointer is represented implicitly as being over the cell to the right of the current state symbol (so for example, if the row is $#w _ 1 w _ 2 q _ i w _ 3#$, this represents that the tape’s contents are $w _ 1 w _ 2 w _ 3$ and the pointer is over $w _ 3$).

Say a tableau is accepting if any row of the tableau is an accepting configuration, so that every accepting tableau for $N$ on $w$ corresponds to an accepting computation branch of $N$ on $w$.

Since $\mathsf{TQBF}$ is $\mathsf{PSPACE}$-complete under log-space $m$ reductions, if $\mathsf{TQBF}$ were in $\mathsf L$, it would imply that $\mathsf{PSPACE} = \mathsf L$, which contradicts the space hierarchy theorem.