Galois Theory HT25, Bounds on the size of the Galois group
Flashcards
$G$ is finite
Suppose:
- $G$ is a (possibly infinite) group
- $X$ is a finite set
- There exists $x \in X$ such that $\text{Stab} _ G(x)$ is a finite set
@Prove that then $G$ is finite.
$G \cdot x$ is finite since $X$ is finite (there’s only finitely many places that can be mapped onto). Let $G \cdot x = \{g _ 1 \cdot x, \ldots, g _ n \cdot x\}$. Then:
\[\pi _ x^{-1}(g _ i \cdot x) = g _ i \text{Stab} _ G(x)\]which is a finite set for each $i$, by assumption.
But then:
\[G = \pi _ x^{-1} (g _ 1 \cdot x) \cup \cdots \cup \pi _ x^{-1}(g _ n \cdot x)\]This is a finite union of finite sets and is therefore finite.
Suppose that $K/F$ is a finite extension. @State a basic result about the corresponding Galois group $\text{Gal}(K/F)$?
It is also finite.
@Prove that if $K/F$ is a finite extension then $G := \text{Gal}(K/F)$ is finite.
Let $\{\alpha _ 1, \ldots, \alpha _ n\}$ be a basis for $K$ as an $F$-vector space. Each $\alpha _ i$ is algebraic over $F$ by the result that says
Suppose:
- $K/F$ is a finite field extension
- $\alpha \in K$
Then $\alpha$ is algebraic over $F$.
Let $m _ i := m _ {F, \alpha _ i}$ be the minimal polynomial of each $\alpha _ i$ over $F$, and consider the corresponding finite sets of roots $V(m _ i) := \{\beta \in K \mid m _ i(\beta) = 0\}$. Then consider the induced “diagonal action” of $G$ on the set $X = V(m _ 1) \times \cdots V(m _ n)$.
We’re looking to apply the result that says:
Suppose:
- $G$ is a (possibly infinite) group
- $X$ is a finite set
- There exists $x \in X$ such that $\text{Stab} _ G(x)$ is a finite set
Then $G$ is finite.
Note that $\text{Stab} _ G((\alpha _ 1, \ldots, \alpha _ n)) = \{1\}$, since if it fixes each $\alpha _ i$ it must fix every element of $K$ as $\{\alpha _ 1, \ldots, \alpha _ n\}$ is an $F$-vector space basis for $K$. But if it fixes every element, it is the identity map. So we have found an element of $x \in X$ such that $\text{Stab} _ G(x)$ is a finite set, and hence $G$ must also be finite.
It follows that $\text{Gal}(K/F)$ is finite.
If $K/F$ finite, then $G$ is smaller than the size of the field extension
Suppose:
- $K/F$ is a finite field extension
- $F$ is infinite
- $K _ 1, \ldots, K _ m$ are finitely many proper subfields of $K$ containing $F$.
@State a result about the union of these subfields.
This result is useful in proving that $ \vert G \vert \le [F(z) : F]$ where $z \in K$ has $\text{Stab} _ G(z) = \{1\}$ in the case where $F$ is infinite. Here you apply it to pick some $z \in K \setminus (K^{\langle g _ 1 \rangle} \cup \cdots \cup K^{\langle g _ n \rangle})$.
Suppose:
- $K/F$ is a finite field extension
- $F$ is infinite
- $K _ 1, \ldots, K _ m$ are finitely many proper subfields of $K$ containing $F$.
@Prove that then:
\[K _ 1 \cup \cdots \cup K _ m < K\]
Overall idea: Aim to contradict the minimality of $m$ if $K = K _ 1 \cup \cdots \cup K _ m$. Consider $x + \alpha y$ where $x \in K _ 1$, $y \in K \setminus K _ 1$, and $m+1$ different $\alpha \in K$. Then for injectivity reasons there must be some $x + \alpha y$ and $x + \beta y$ where $x$ and $y$ both lie in $K _ {i(\alpha)}$; this can be used to find a contradiction.
Suppose for a contradiction that $K = K _ 1 \cup \cdots \cup K _ m$. We can assume that $m \ge 2$ (otherwise it is trivial) and that $m$ is minimal with this property (otherwise combine two subsets together).
Choose $y \in K \setminus K _ 1$. We aim to show that $K _ 1 \subseteq K _ 2 \cup \cdots \cup K _ m$, since that implies $K = K _ 2 \cup \cdots \cup K _ m$, which contradicts the minimality of $m$.
Let $x \in K _ 1$. Since $F$ is infinite, there exists a finite subset $S \subset F$ where $ \vert S \vert = m+1$.
Then for each $a \in S$, there is some $i(\alpha) \in \{1, \ldots, m\}$ such that $x + \alpha y \in K _ {i(\alpha)}$ by the assumption that $K _ 1, \ldots, K _ m$ cover $K$.
$i : S \to \{1, \ldots, m\}$ cannot be injective since $ \vert S \vert = m+1$.
Hence $\exists \alpha, \beta \in S$ such that $\alpha \ne \beta$ and $x + \alpha y$ and $x + \beta y$ both lie in $K _ {i(\alpha)}$.
But since
\[y = \frac{(x + \alpha y) - (x + \beta y)}{\alpha - \beta}\]It must be the case that $y \in K _ {i(\alpha)}$. But as $y \notin K _ 1$ by assumption, $i(\alpha) > 1$.
But since
\[x = (x + \alpha y) - \alpha y \in K _ {i(\alpha)}\]and $K _ {i(\alpha)} \subseteq K _ 2 \cup \ldots \cup K _ m$ for each $x \in K _ 1$, it follows $K _ 1 \subseteq K _ 2 \cup \cdots \cup K _ m$, contradicting the minimality of $m$.
Suppose:
- $K/F$ is a finite field extension
- $G = \text{Gal}(K/F)$
- $z \in K$ has $\text{Stab} _ G(z) = \{1\}$
@State a result on the size of $G$.
Suppose:
- $K/F$ is a finite field extension
- $G = \text{Gal}(K/F)$
- $z \in K$ has $\text{Stab} _ G(z) = \{1\}$
@Prove that:
\[|G| \le [F(z) : F]\]
Define
\[V(m _ {F,z}) := \lbrace k \in K \mid m _ {F,z}(k) = 0\rbrace\]Then
\[\begin{aligned} |G| &= |G\cdot z | \times |\text{Stab} _ G(z)| &&\text{(orbit-stab)} \\\\ &= |G\cdot z| \times 1 &&(\text{assump. in question}) \\\\ &\le |V(m _ {F,z})| &&(\star 1) \\\\ &\le \deg(m _ {F,z}) &&(\text{fundamental theorem of algebra}) \\\\ &= [F(z) : F] &&(\star 2) \end{aligned}\]where:
- $(\star 1)$ is justified like so: $G \cdot z$ is the orbit of $z$ under $G$. Since $z \in V(m _ {F, z})$ and the action on $K$ restricts to one on $V(m _ {F, z})$, any element of $G$ must send $z$ back into $V(m _ {F, z})$. So $G \cdot z$ can be no bigger than the size of $V(m _ {F, z})$.
- $(\star 2)$ is justified by the general result that the degree of the field extension is equal to the degree of the minimal polynomial.
Suppose:
- $K / F$ is a finite field extension
- $G = \text{Gal}(K/F)$
@State a bound on the size of $G$.
We would like to be able to say that if:
- $K/F$ is a finite field extension
- $G = \text{Gal}(K/F)$
then:
\[|G| \le [K : F]\]
There is a result which says:
If:
- $K/F$ is a finite field extension
- $G = \text{Gal}(K/F)$
- $z \in K$ has $\text{Stab} _ G(z) = \{1\}$
then:
\[\vert G \vert \le [F(z) : F]\]
which would then imply $ \vert G \vert \le [K : F]$ as $[F(z) : F] \le [K : F]$. So we need to satisfy the extra hypothesis that there is some $z \in K$ where $\text{Stab} _ G(z) = 1$.
@Prove that there always exists some $z$ satisfying this extra hypothesis.
If:
- $K/F$ is a finite field extension
- $G = \text{Gal}(K/F)$
- $z \in K$ has $\text{Stab} _ G(z) = \{1\}$
then:
$G$ is finite by the result that says finite field extensions lead to finite Galois groups (reminder: this is a result that comes from considering how $G$ acts on $V(m _ {\alpha _ 1}) \times \cdots \times V(m _ {\alpha _ n})$). We consider two cases, one where $F$ is infinite, and one where $F$ is finite.
Case 1: $F$ infinite.
Write $G = \{1, g _ 1, \ldots, g _ n\}$ where $g _ i$ distinct.
Since each $g _ i$ is non-trivial, each $K^{\langle g _ i \rangle}$ is a proper subfield of $K$ containing $F$. Since $F$ is infinite, there exists some $z$ in the set
\[K \setminus (K^{\langle g _ 1\rangle} \cup \cdots \cup K^{\langle g _ n \rangle})\]by the result that says
\[K _ 1 \cup \cdots \cup K _ m < K\]If:
- $K/F$ is a finite field extension
- $F$ is infinite
- $K _ 1, \ldots, K _ m$ are finitely many proper subfields of $K$ containing $F$.
then:
But this means that $z$ is not fixed by any $g _ i$, so the only element of $G$ fixing $z$ is $1$.
Case 2: $F$ finite.
Note that $K^\times$ is a finite abelian group. Hence by the structure theorem,
\[K^\times \cong \left( \frac{\mathbb Z}{p _ i \mathbb Z} \right)^{k _ 1} \times \cdots \times \left( \frac{\mathbb Z}{p _ n \mathbb Z} \right)^{k _ n}\]In fact, $k _ i = 1$ for all $i$. If $k _ i > 1$, then it would contain a subgroup of the form $\left(\frac{\mathbb Z}{p _ i \mathbb Z}\right)^2$. All elements of the subgroup must satisfy $x^{p _ i} = 1$. Therefore all elements are roots of $x^{p _ i} - 1$, but $x^{p _ i} - 1$ has at most $p _ i$ roots, not $p _ i^2$. Hence each $k _ i = 1$.
This implies that
\[K^\times \cong \frac{\mathbb Z}{p _ i \mathbb Z} \times \cdots \times \frac{\mathbb Z}{p _ n \mathbb Z}\]and hence
\[K^\times \cong \frac{\mathbb Z}{p _ 1 \cdots p _ n \mathbb Z}\]and so $K = \langle z \rangle$ for some $z \in K$. Hence if $\varphi \in \text{Stab} _ G(z)$, then $\varphi(z) = z$ and $\varphi$ fixes all of $K$, so $\varphi = \text{id}$. Hence we have found the required $z$.
(this is pretty much just a proof that all finite extensions of finite fields are simple, and then using the fact that the generator has the required property).
If $K/F$ Galois, then $G$ is larger than the size of the field extension
Suppose:
- $\varphi : F \to \tilde F$ is an isomorphism between two fields
- $K / F$ and $\tilde K / \tilde F$ are finite extensions
- $\alpha \in K$, $\tilde \alpha \in \tilde K$
- $\varphi(m _ {F, \alpha})(\tilde \alpha) = 0$
@State a useful result in this context.
There is a unique extension of $\varphi$ to $\varphi^\ast$ where
\[\varphi^\ast : F(\alpha) \to \tilde F(\tilde \alpha)\]such that $\varphi^\ast (\alpha) = \tilde \alpha$.
In other words, if you’ve got an isomorphism between two fields, and two elements of an extension with the important “minimal polynomial preserving” property, then it extends to a field extension of the field adjoined with these two elements. This could be summarised by the diagram:
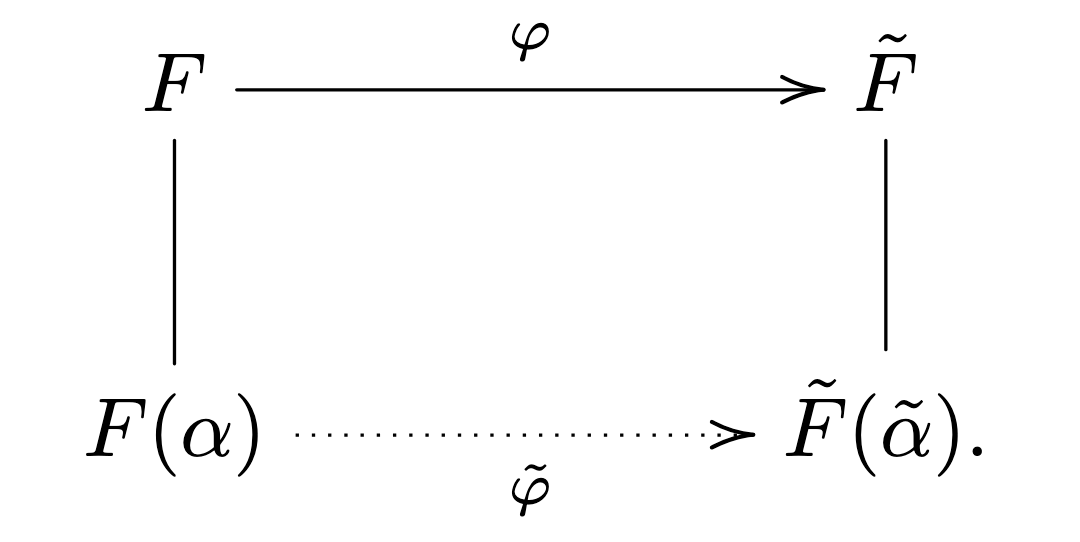
Suppose:
- $\varphi : F \to \tilde F$ is an isomorphism between two fields
- $K / F$ and $\tilde K / \tilde F$ are finite extensions
- $\alpha \in K$, $\tilde \alpha \in \tilde K$
- $\varphi(m _ {F, \alpha})(\tilde \alpha) = 0$
@Prove that then there is a unique extension of $\varphi$ to
\[\varphi^\ast : F(\alpha) \to \tilde F(\tilde \alpha)\]
such that $\varphi^\ast (\alpha) = \tilde \alpha$.
Existence. By assumption, $\varphi(m _ {F, \alpha})(\tilde \alpha) = 0$. Then $\varphi(m _ {F, \alpha}) \mid m _ {\tilde F, \tilde \alpha}$, but as $m _ {\tilde F, \tilde \alpha}$ is irreducible, it follows that $\varphi(m _ {F, \alpha}) = m _ {\tilde F, \tilde \alpha}$.
We have the isomorphisms
\[\begin{aligned} &\theta : \frac{F[t]}{\langle m _ {F, \alpha} \rangle} \stackrel\cong\longrightarrow F(\alpha) \\\\ &\tilde \theta : \frac{\tilde F[t]}{\langle m _ {\tilde F, \tilde \alpha}\rangle} \stackrel\cong\longrightarrow\tilde F(\tilde \alpha) \end{aligned}\]And $\varphi : F \to \tilde F$ extends to an isomorphism
\[\varphi' : F[t] \stackrel\cong\longrightarrow\tilde F[t]\]by fixing $t$. As $\varphi’$ sends $\langle m _ {F, \alpha}\rangle$ to $\langle m _ {\tilde F, \tilde \alpha} \rangle$, by the universal property of quotients this map descends to give
\[\overline \varphi : \frac{F[t]}{\langle m _ {F, \alpha}\rangle} \longrightarrow \frac{\tilde F[t]}{\langle m _ {\tilde F, \tilde \alpha}\rangle}\]Chaining isomorphism together, we have
\[\begin{aligned} &\varphi^\ast : F(\alpha) \to \tilde F(\tilde \alpha) \\\\ &\varphi^\ast := \tilde \theta \circ \overline \varphi \circ \theta^{-1} \end{aligned}\]and this gives the existence of the required isomorphism (note also that $\alpha$ is mapped to $\tilde \alpha$ as required, since $t$ is mapped to/from $\alpha$ or $\tilde \alpha$).
This can be summarised with the following commutative diagram, where $\tilde \varphi$ should be replaced by $\varphi^\ast$.
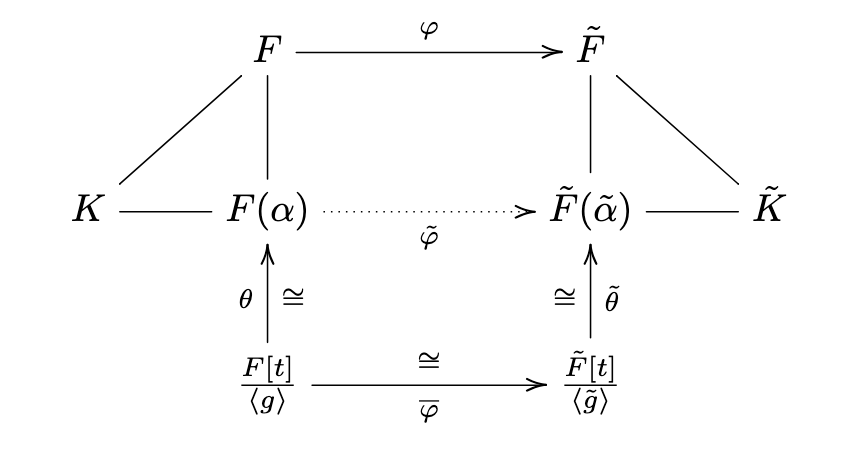
Uniqueness. Suppose that $\psi : F(\alpha) \to \tilde F(\tilde \alpha)$ is another isomorphism with the property that $\psi(\alpha) = \tilde \alpha$ (this is what we are assuming in the construction).
Then $\psi$ agrees with $\varphi^\ast$ on $F$ and $\alpha$.
Since $F$ and $\alpha$ generate $F[\alpha]$, and $F[\alpha] = F(\alpha)$ ($\alpha$ is algebraic) it follows that $\psi = \varphi^\ast$, so we have uniqueness as required.
Suppose:
- $\varphi : F \to \tilde F$ is an isomorphism of fields
- $f \in F[t]$ is a separable polynomial
- $K$ is a splitting field for $f$
- $\tilde f = \varphi(f)$
- $\tilde K$ is a splitting field for $\tilde f$
@State a result about the number of distinct isomorphisms $K \to \tilde K$ extending $\varphi$.
There are at least $[K : F]$ distinct isomorphisms extending $\varphi$ to an isomorphism $\phi’ : K \to \tilde K$.
Suppose:
- $\varphi : F \to \tilde F$ is an isomorphism of fields
- $f \in F[t]$ is a separable polynomial
- $K$ is a splitting field for $f$
- $\tilde f = \varphi(f)$
- $\tilde K$ is a splitting field for $\tilde f$
@Prove that there are at least $[K : F]$ distinct isomorphisms extending $\varphi$ to an isomorphism $\phi’ : K \to \tilde K$.
Overall idea: Inductively build on a previous result that establishes extensions of isomorphisms to $F(\alpha) \to F(\tilde \alpha)$ under the assumption that $\varphi(m _ {F, \alpha})(\tilde \alpha) = 0$. This is done by applying the result to the roots of $f$.
We proceed by induction on $[K : F]$.
Base case: $[K:F] = 1$. Then $K \cong F$, so the chain of isomorphisms $K \cong F \cong \tilde F \cong \tilde K$ gives at least one isomorphism $K \to \tilde K$.
Inductive step: Let $g$ be a monic irreducible factor of $f$ in $F[t]$ with $\deg g \ge 2$. Then $g$ is separable in $F[t]$. (it’s not necessary to assume that the field is of characteristic zero, since one of the assumptions above is that $f$ is separable).
Then $\tilde g := \varphi(g)$ is also separable (since if it weren’t this would also imply $g$ wasn’t).
Since $\tilde K$ is a splitting field of $\tilde f$ and $\tilde g \mid \tilde f$, $\tilde g$ has exactly $n := \deg \tilde g$ roots, say $\beta _ 1, \ldots, \beta _ n \in \tilde K$ by the result that all roots of separable irreducible polynomials are simple.
Choose a root $\alpha \in K$ of $g$. Since $g(\alpha) = 0$, by the “division property” of minimal polynomials, $m _ {F, \alpha} \mid g$. But then by assumption $g$ is monic and irreducible over $F$, so it must actually be the case $m _ {F, \alpha} = g$.
Pick some $i = 1, \ldots, n$. Then $\phi(m _ {F, \alpha})(\beta _ i) = \phi(g)(\beta _ i) = \tilde g(\beta _ i) = 0$, so the conditions of the lemma that
\[\varphi^\ast : F(\alpha) \to \tilde F(\tilde \alpha)\]If
- $\varphi : F \to \tilde F$ is an isomorphism between two fields
- $K / F$ and $\tilde F / \tilde K$ are finite extensions
- $\alpha \in K$, $\tilde \alpha \in \tilde K$
- $\varphi(m _ {F, \alpha})(\tilde \alpha) = 0$
Then there is a unique extension of $\varphi$ to
such that $\varphi^\ast (\alpha) = \tilde \alpha$.
are satisfied (where $\alpha$ is also $\alpha$ in the above, and $\beta _ i$ plays the role of $\tilde \alpha$) . Hence we obtain a unique isomorphism $\phi _ i : F(\alpha) \to \tilde F(\beta _ i)$ which extends $\phi : F \to \tilde F$ and sends $\alpha$ to $\beta _ i$.
Let $m := [K : F(\alpha)]$. As $m < [K : F]$, we can apply the inducitve hypothesis to $K/F(\alpha)$ and $\tilde K / \tilde F(\beta _ i)$ together with the isomorphism to find at least $m$ different extensions
\[\phi _ i^{(j)} : K \to \tilde K \quad\text{ for }j = 1, \ldots, m\]It remains to show that these are all distinct. If $\phi _ {i}^{(j)} = \phi _ {i’}^{(j’)}$ for some $1 \le i, i’ \le n$ and $1 \le j, j’ \le m$, we have
\[\begin{aligned} \beta _ i &= \phi _ i^{(j)}(\alpha) \\\\ &= \phi _ {i'}^{(j')}(\alpha) \\\\ &= \beta _ {i'} \end{aligned}\]So $i = i’$ and by induction $j = j’$ (since they are distinct in the base case and the inductive hypothesis guarantees the distinctness of the isomorphisms $K/F(\alpha) \to \tilde K / \tilde F(\beta _ i)$ for each fixed $i$).
Therefore there are at least $mn$ different extensions ($n$ for the initial choice of $\beta _ i$, and $m$ constructed inductively).
Since $[F(\alpha):F] = \deg m _ {F, \alpha} = \deg g = \deg \tilde g = n$, it follows that $[K : F] = [K : F(\alpha)] [F(\alpha) : F] = mn$ and we are done.
We have a result that says if:
- $\varphi : F \to \tilde F$ is an isomorphism of fields
- $f \in F[t]$ is a separable polynomial
- $K$ is a splitting field for $f$
- $\tilde f = \varphi(f)$
- $\tilde K$ is a splitting field for $\tilde f$
then there are at least $[K : F]$ distinct isomorphisms extending $\varphi$. Use this to @state and @prove a result about the size of the Galois groups of Galois extensions.
Suppose:
- $K/F$ is a Galois extension
Then:
\[|\text{Gal}(K/F)| \ge [K : F]\]Proof: Since $K/F$ is a Galois extension, by definition $K$ is the splitting field for some polynomial $f \in F[t]$. In the above result, take $\tilde F := F$ and $\varphi : F \to \tilde F$ as the identity map. Then there are at least $[K : F]$ distinct automorphisms of $K$ extending $1 : F \to F$.
Automorphisms of this type are exactly the $F$-linear automorphisms of $K$, and hence
\[|\text{Gal}(K/F)| \ge [K : F]\]as required.
Suppose:
- $K/F$ is a finite field extension
- $\alpha, \beta \in K$
- $f(x) \in K[x]$ is irreducible and $f(\alpha) = f(\beta) = 0$
Can you give a @counterexample to show that it need not be the case that there is always an automorphism $\sigma \in \text{Aut} _ F(K)$ such that $\sigma(\alpha) = \beta$?
Consider:
- $K = \mathbb Q(\sqrt[4]{2})$
- $F = \mathbb Q$
- $\alpha = \sqrt 2$
- $\beta = -\sqrt 2$
- $f(x) = x^2 - 2$
Clearly all conditions are satisfied. But you may compute $\text{Aut} _ F(K)$ as $\lbrace \text{id}, \tau \rbrace$ where $\tau$ is the transposition $\sqrt[4]{2} \mapsto -\sqrt[4]{2}$, and hence $\tau(\sqrt 2) = \tau(\sqrt[4]{2} \sqrt[4]{2}) = \tau(\sqrt[4]{2}) \tau(\sqrt[4]{2}) = \sqrt 2$, and so no such automorphism exists.
@example~ @exam~
Combing these bounds
Suppose:
- $K/F$ is a Galois extension
@State a result about the size of the Galois group $\text{Gal}(K/F$)?
Suppose:
- $K/F$ is a Galois extension
@State the two results together which allow you to @prove that $ \vert \text{Gal}(K/F) \vert = [K : F]$.
\[\vert \text{Gal}(K/F) \vert \ge [K : F]\]Suppose:
- $K/F$ is a Galois extension
Then:
and
\[\vert \text{Gal}(K/F) \vert \le [K : F]\]Suppose:
- $K/F$ is a finite field extension
Then:
@Prove that if:
- $K/F$ is a Galois extension
- $G = \text{Gal}(K/F)$
Then:
\[\text{Gal}(K/K^G) = G\]
- $\text{Gal}(K/K^G) \subseteq G$: $K^G$ is a subfield containing $F$, so every $K^G$-linear automorphism $\sigma$ of $K$ is also $F$-linear, hence $\sigma \in G$.
- $\text{Gal}(K/K^G) \supseteq G$: If $\sigma : K \to K$ is $F$-linear, then $\sigma \in G$ and so $\sigma$ fixes $K^G$ pointwise. Therefore $\sigma$ is also $K^G$-linear.
More general result that is a precursor to Artin’s lemma
See also [[Notes - Galois Theory HT25, Artin’s lemma]]U.
Suppose:
- $K$ is a field
- $H \le \text{Aut} _ \text{Rings}(K)$ finite subgroup
@State a result about the size of $H$.
@Prove that if:
- $K$ is a field
- $H \le \text{Aut} _ \text{Rings}(K)$ is a finite subgroup
then:
- $[K : K^H] \le \vert H \vert $
Suppose not. Then there exists a sequence $\alpha _ 1, \ldots, \alpha _ d$ of elements of $K$ which is linearly independent over $K^H$ and such that $d > \vert H \vert $.
Let $n := \vert H \vert $ and suppose $\sigma _ 1, \ldots, \sigma _ n \in H$ is an enumeration of the elements of $H$. Consider the matrix
\[\left( \begin{array}{cccc} \sigma _ 1(\alpha _ 1) & \sigma _ 1(\alpha _ 2) & \cdots & \sigma _ 1(\alpha _ d) \\\\ \sigma _ 2(\alpha _ 1) & \sigma _ 2(\alpha _ 2) & \cdots & \sigma _ 2(\alpha _ d) \\\\ \vdots & \vdots & \ddots & \vdots \\\\ \sigma _ n(\alpha _ 1) & \sigma _ n(\alpha _ 2) & \cdots & \sigma _ n(\alpha _ d) \end{array} \right)\]Note that the columns of this matrix are linearly dependent over $K$ (as $n < d$, so this matrix has more columns than rows), and hence there exists a sequence $\beta _ 1, \ldots, \beta _ d \in K$ where at least one $\beta _ i$ does not vanish such that
\[\sum^d _ {i = 1} \beta _ i \sigma _ k(\alpha _ i) = 0\]for each $1 \le k \le n$ (since there is a linear combination of columns that makes zero).
Choose the sequence $\beta _ 1, \ldots, \beta _ d$ so that the quantity
\[r := |\lbrace i \in \lbrace 1, \ldots, d \rbrace \mid \beta _ i \ne 0 \rbrace|\]is minimal. Relabelling and dividing by $\beta _ r$, we may assume that $\beta _ 1, \ldots, \beta _ r \ne 0$ and that $\beta _ {r+1}, \beta _ {r+2}, \ldots, \beta _ {d} = 0$, and that $\beta _ r = 1$.
By the assumption that the $\alpha _ 1, \ldots, \alpha _ d$ are linearly independent over $K^H$, there exists $i _ 0 \in \lbrace 1, \ldots, r \rbrace$ such that $\beta _ {i _ 0} \not\in K^H$ (and in particular, $r > 1$ since $i _ 0 \ne r$). Relabelling, we may assume that $\beta _ 1 \notin K^H$. Let $\sigma’$ be such that $\sigma’(\beta _ 1) \ne \beta _ 1$ (this must exist, as $\beta _ 1$ is not in the fixed field of $H$). Then for each $1 \le k \le n$:
\[\begin{aligned} \sum^d _ {i = 1} \beta _ i \sigma _ k(\alpha _ i) = 0 &\implies \sum^d _ {i = 1} \sigma'(\beta _ i \sigma _ k(\alpha _ i)) = 0 \\\\ &\implies \sum^d _ {i = 1} \sigma'(\beta _ i) \sigma _ k (\alpha _ i) = 0 &&(\text{relabel } k)\\\\ &\implies \sum^d _ {i = 1} (\sigma'(\beta _ i) - \beta _ i)\sigma _ k(\alpha _ i) = 0 &&(\text{subtract original sum}) \\\\ &\implies \sum^{r-1} _ {i = 1} (\sigma'(\beta _ i) - \beta _ i)\sigma _ k(\alpha _ i) = 0 &&(\star) \end{aligned}\]where $(\star)$ is justified as $\beta _ {r+1} = \cdots = \beta _ d = 0$ implies that $\sigma’(\beta _ i) = 0$ and therefore $\sigma’(\beta _ i) - \beta _ i = 0$ for each $i > r$. But since $\beta _ r = 1$ and any automorphism $\sigma’$ must fix $1$, it also follows that $\sigma’(\beta _ r) - \beta _ r = 1 - 1 = 0$.
However, since $\sigma _ {k _ 0}(\beta _ 1) \ne \beta _ 1$, this contradicts the minimality of $r$. Hence we cannot have that $d > n$, as required.