Galois Theory HT25, Finite fields

\[|F| = p^n\]

for some prime $p$ and positive integer $n$.

Since $F$ is finite, it must have positive characteristic.

Since $F$ is a field, the characteristic must be a prime $p$.

Hence $F$ contains a copy of $\mathbb F _ p$, generated by the identity.

Considering $F$ as a vector space over $\mathbb F _ p$, note that since $F$ is finite, it must have a finite dimension $n$. Therefore $ \vert F \vert = p^n$.

\[\phi : F \to F\]

defined by

\[\phi(x) := x^p\]

for all $x \in F$.

$\phi$ is multiplicative: $\phi(xy) = (xy)^p = x^p y^p$.

$\phi$ is additive: This is the “Freshman’s dream”: by the binomial theorem,

\[(x+y)^p = \sum^p_{i = 0} {p \choose i} x^p y^{p-i}\]

Since $p \mid {p \choose i}$ for all $0 < i < p$, it follows that

\[(x + y)^p = x^p + y^p\]

$\phi$ is injective: Suppose that $\phi(a) = \phi(b)$. Then $\phi(a - b) = 0$. Since $F$ is in particular an integral domain, it follows that $a - b = 0$, and so $a = b$.

$\phi$ is surjective: $F$ is finite, so injectivity implies surjectivity.

$\phi$ is $\mathbb F _ p$-linear: $\phi(x) = x^p = x$ for all $x \in \mathbb F _ p$ by Fermat’s Little Theorem. Hence $\phi \in \text{Gal}(F/\mathbb F _ p)$.

The Frobenius endomorphism $x \mapsto x^p$ is always in $\text{Gal}(F / \mathbb F _ p)$.

If $\alpha$ is a root of $f$, then repeatedly applying the Frobenius endomorphism to this root tells you that $\alpha, \alpha^p, \alpha^{p^2}, \ldots$ are all roots.

A field is of order $p^n$ iff it is a splitting field of $t^{p^n} - t$ over $\mathbb F _ p$.

Let $F$ be the field under consideration and $f(t) = t^{p^n} - t \in \mathbb F _ p[t]$.

(1) Any field of order $p^n$ is a splitting field of $t^{p^n} - t$ over $\mathbb F _ p$:

$F$ must contain a copy of $\mathbb F _ p$. Then $x^{p^n - 1} = 1$ for all $x \in F^\times$ by Lagrange’s Theorem.

Therefore all elements of $F$ are roots of $t^{p^n} - t$. Therefore $t^{p^n} - t$ splits completely in $F[t]$ and its roots generate $F$, and hence $F$ is a splitting field of $t^{p^n} - t$ over $\mathbb F _ p$.

---

(2) Any splitting field of $t^{p^n} - t$ over $\mathbb F _ p$ is a field of order $p^n$:

Note $f$ is separable and therefore has exactly $p^n$ distinct roots. Let $V$ be the set of roots of $f$ in $F$. Then $ \vert V \vert = p^n$ and

\[V = \\{\alpha \in F : \alpha^{p^n} = \alpha\\} = F^{\langle \phi^n \rangle}\]

where $\phi$ is the Frobenius endomorphism. Since $F$ is a splitting field of $f$ by assumption, $V$ generates $F$ as a field, and so $V = F$.

Hence $ \vert F \vert = \vert V \vert = p^n$.

(1): There is a result that says

Any field of order $p^n$ is a splitting field of $t^{p^n} - t$ over $\mathbb F _ p$.

But there is another result that says:

Any two splitting fields of a polynomial are isomorphic.

(2): If $g$ is an irreducible factor of $t^{p^n} - t$, then $g$ has no repeated roots in any splitting field. Therefore $g$ is separable by the result that says

If:

• $X \subseteq L$

Then the polynomial $f _ X := \prod _ {y \in X} (t - y) \in L[t]$ is always separable.

Hence all factors of $t^{p^n} - t$ are separable, and so $t^{p^n} - t$ is separable. But by the theorem that says

Any splitting field of $t^{p^n} - t$ over $\mathbb F _ p$ is a field of order $p^n$.

$\mathbb F _ {p^n}$ is a splitting field of the separable polynomial $t^{p _ n} - t$ and is hence Galois over $\mathbb F _ p$.

Since $\alpha^{p^n} = \alpha$ for all $\alpha \in \mathbb F _ {p^n}$ by Fermat’s Little Theorem, it follows that $\phi^n = 1$.

Now suppose that $\phi^m = 1$ for some $1 \le m \le n$. Then $\alpha^{p^m} = \alpha$ for all $\alpha \in \mathbb F _ {p^n}$. But then $t^{p^m} - t$ has $ \vert \mathbb F _ {p^n} \vert $ distinct roots in $\mathbb F _ {p^n}$, which implies that $p^m \ge p^n$. Hence $m \ge n$, and the order of $\phi$ is precisely $n$.

Since $ \vert \text{Gal}(\mathbb F _ {p^n} / \mathbb F _ p) \vert = [\mathbb F _ {p^n} : \mathbb F _ p] = n$, it follows that $\text{Gal}(\mathbb F _ {p^n} / \mathbb F _ p) \cong C _ n$.

It is cyclic of order $n$, and is generated by the Frobenius endomorphism $\phi : \mathbb F _ {p^n} \to \mathbb F _ {p^n}$.

The field must be of order $p^n$, and every finite field of order $p^n$ is the splitting field of $x^{p^n} - x$ over $\mathbb F _ p$.

$\mathbb F _ {p^a}$ embeds into $\mathbb F _ {p^b}$ if and only if $a \mid b$.

Forward direction: Suppose that $\mathbb F _ {p^a}$ embeds into $\mathbb F _ {p^b}$. Let $G = \text{Gal}(\mathbb F _ {p^b}/\mathbb F _ p)$, then $G$ is cyclic by the result that says

The Galois group $\text{Gal}(\mathbb F _ {p^n} / \mathbb F _ p)$ is cyclic of order $n$, and is generated by the Frobenius endomorphism $\phi : \mathbb F _ {p^n} \to \mathbb F _ {p^n}$.

and has order $b$. Let $H = \text{Gal}(\mathbb F _ {p^b} / \mathbb F _ {p^a})$ be the subgroup of $G$ corresponding to $\mathbb F _ {p^a}$ (which exists by the Galois correspondence). Since $G$ is abelian, $H$ is normal and $G/H \cong \text{Gal}(\mathbb F _ {p^a} / \mathbb F _ p)$. But then by the above result, $G/H$ is also a cyclic group of order $a$.

But then $a \mid b$ by Lagrange’s theorem.

In pictures:

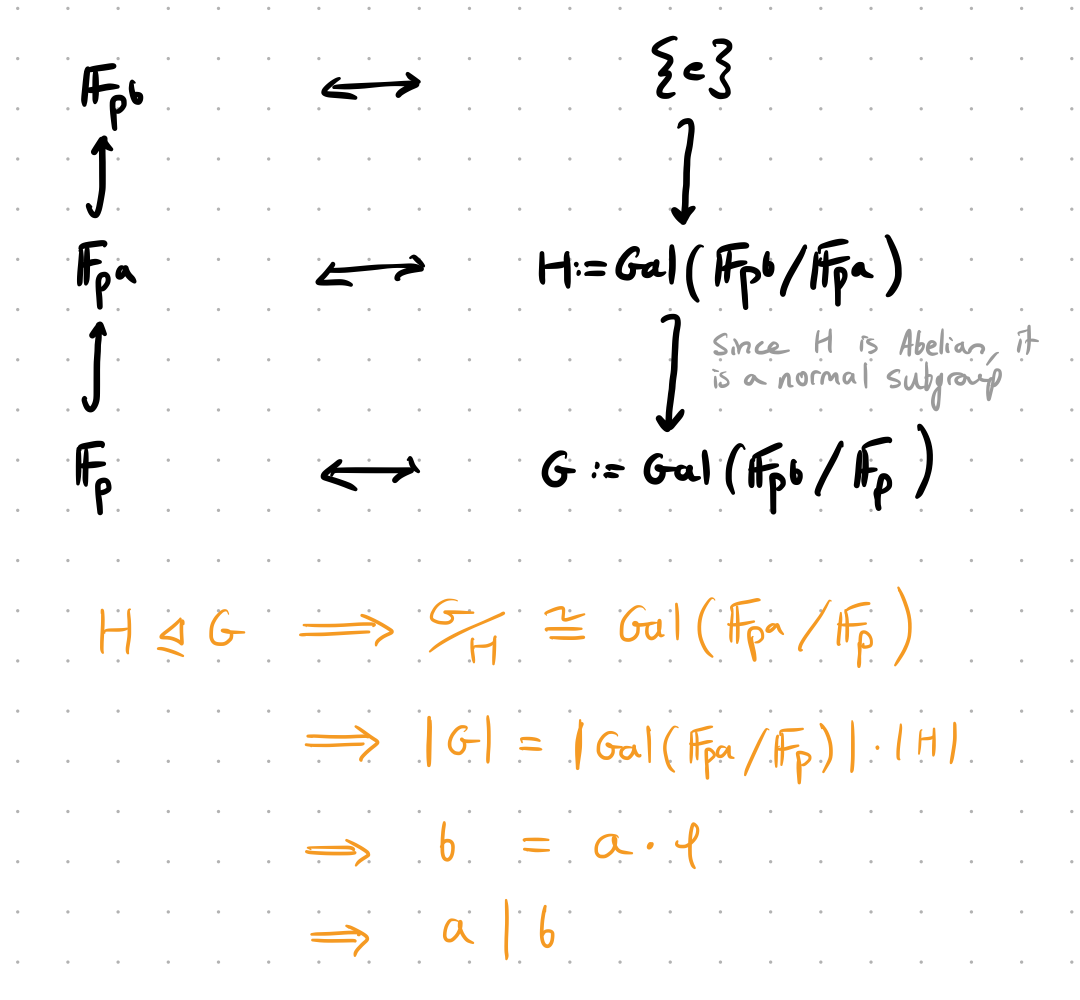
Backward direction: Suppose that $a \mid b$. Then $p^a - 1 \mid p^b - 1$ (this can be seen by considering $b = ka$ and then expanding as a sum of powers, full justification at end). Then similarly,

\[t^{p^a - 1} - 1 \mid t^{p^b - 1} - 1\]

Multiplying through by $t$, we see

\[t^{p^a} - t \mid t^{p^b} - t\]

Therefore $t^{p^a} - t$ splits completely in $\mathbb F _ {p^b}[t]$ (since previous results tell us that $t^{p^b} - t$ splits completely in this field). But then it follows that $\mathbb F _ {p^a}$ embeds into $\mathbb F _ {p^b}$ by the result that says

Let $f \in F[t]$ be a separable polynomial, and let $K$ be a splitting field for $f$. Suppose that $L$ is another extension of $F$ such that $f$ splits completely in $L[t]$. Then there exists at least one injective homomorphism $K \hookrightarrow L$.

it follows that $\mathbb F _ {p^a}$ embeds into $\mathbb F _ {p^b}$.

---

Why $a \mid b$ implies $p^a - 1 \mid p^b - 1$:

\[\begin{aligned} a \mid b &\implies b = ka \\\\ &\implies p^b - 1 = p^{ka} -1 = (p^k)^a - 1 \\\\ &\implies p^b - 1 = (p^a - 1)(1 + p^a + (p^a)^2 + \cdots + (p^a)^{k-1}) \\\\ &\implies p^a - 1 \mid p^b - 1 \end{aligned}\]

The multiplicative group of a finite field is cyclic.

Let $G$ be the multiplicative group and $ \vert G \vert = n$. Let $d$ be a divisor of $n$ and let $\psi(d)$ be the number of elements of order $d$ in $G$.

---

Since $G$ is a finite abelian group,

\[G \cong \left(\frac{\mathbb Z}{p_1 \mathbb Z}\right)^{k_1} \times \cdots \times \left(\frac{\mathbb Z}{p_n \mathbb Z}\right)^{k_n}\]

by the primary decomposition form of the structure theorem for finitely generated abelian groups.

Then $k _ i = 1$ for all $i$. Assume, for a contradiction, that $k _ i > 1$ for some $i$. This implies $K^\times$ contains a subgroup of the form $\left( \mathbb Z / p _ i \mathbb Z \right)^2$. All elements of this subgroup must satisfy $x^{p _ i} = 1$, and hence must satisfy $x^{p _ i} - 1 = 0$. But $x^{p _ i} - 1$ has at most $p _ i$ roots, not $p _ i^2$. Hence each $k _ i = 1$.

Thus

\[\begin{aligned} G &\cong \frac{\mathbb Z}{p_1 \mathbb Z} \times \cdots \times \frac{\mathbb Z}{p_n \mathbb Z} \\\\ &\cong \frac{\mathbb Z}{p_1 \cdots p_n \mathbb Z} \end{aligned}\]

and so $G$ is cyclic as required.

---

“Alternative” proof 1:

Suppose there exists an element $a$ of $G$ whose order is $d$. Let $H$ be the subgroup of $G$ generated by $a$. Then every element of $H$ satisfies the equation $x^d = 1$. Since the number of solutions of $x^d - 1 = 0$ is less than or equal to $d$ and the order of $H$ is $d$,

\[H = \\{x \in G \mid x^d - 1 = 0\\}\]

Therefore either $\psi(d) = 0$ or $psi(d) = \phi(d)$ where $\phi(d)$ is the totient function. As

\[\sum_{d \mid n} \psi(d) = n = \sum_{d \mid n}\]

we have $\psi(d) = \phi(d)$ for all $n$. In particular, $\psi(n) = \phi(n)$ and hence there exists an element of order $n$ in $G$.

---

“Alternative” proof 2:

We have the result that $G$ is cyclic iff there is exactly one subgroup for each divisor of $G$. If $G$ is not cyclic, then there are two distinct subgroups $H _ 1, H _ 2 \le G$ of cardinality $M$. Then $ \vert H _ 1 \cup H _ 2 \vert \le M + 1$ as $H _ 1$ and $H _ 2$ are distinct.

Consider $f(x) = x^M - 1 \in F[x]$. Then the set $S$ of the roots contains $H _ 1 \cup H _ 2$ and therefore has cardinality larger than the degree of $f$, a contradiction.

@exam~

$\mathbb F _ 2(\mu _ 4)$ is the splitting field for the polynomial $f(x) = x^4 - 1 \in \mathbb F _ 2[x]$. But over $\mathbb F _ 2$,

\[f(x) = x^4 - 1 = ((x^2)^2 - 1) = ((x - 1)^2)^2 = (x - 1)^4\]

and so $\mu _ 4 = 1$. Thus $[\mathbb F _ 2(\mu _ 4) : \mathbb F] = 1$.

@example~ @exam~

$\mathbb F _ 3(\mu _ {10})$ is the splitting field of $f(x) = x^{10} - 1 \in \mathbb F _ 3$. Note that $f$ has no repeated roots as $\text{gcd}(f, f’) = \text{gcd}(x^{10} - 1, 10x^9) = 1$, and so $\mathbb F _ 3(\mu _ {10})^\ast$ contains a copy of the group $\mu _ {10}(\mathbb F _ 3)$, which is a cyclic group.

Hence $\mathbb F _ 3(\mu _ {10})^\ast$ contains a cyclic subgroup of order 10.

Let $t$ be such that $\mathbb F _ 3(\mu _ {10}) = \mathbb F _ {3^t}$. Then $10 \mid 3^t - 1$. If $10 \mid 3^a - 1$ for some $a \ge 1$, then $x^{10} - 1$ splits in $\mathbb F _ {3^a}$ since then $\mathbb F^\ast _ {3^a}$ contains a cyclic subgroup of order 10. Suppose that $a$ is the smallest $a \ge 1$ such that $10 \mid 3^a - 1$ (i.e. the order of $3$ in $(\mathbb Z/10\mathbb Z)^\ast$).

Then $\mathbb F _ 3(\mu _ {10}) = \mathbb F _ {3^t}$ is a subfield of $\mathbb F _ {3^a}$ (by the uniqueness of splitting fields). Since by construction $t \ge a$ and $t \le a$, it follows $t = a$.

Hence $[\mathbb F _ 3 (\mu _ {10}) : \mathbb F _ 3]$ is the order of $3$ in $(\mathbb Z/10\mathbb Z)^\ast$, which is $4$.

@exam~ @example~

The order of $k$ in $(\mathbb Z / n \mathbb Z)^\ast$.

@exam~

Write $k = s p^i$ where $s$ is coprime to $p$. Then $\mathbb F _ p(\mu _ k)$ is the splitting field of

\[g(x) = x^k - 1 = (x^s - 1)^{p^i}\]

and so $\mathbb F _ p (\mu _ k)$ is the splitting field of

\[f(x) = x^s - 1\]

$f$ is reducible for all primes $p$.

---

If $p = 2$, then $f(x) = x^4$, which is reducible.

So suppose $p \ne 2$ and that $f$ is irreducible. Then $f$ has four distinct roots in the splitting field, and if $\alpha$ is a root, then so $-\alpha$ (since $x$ only appears as $x^2$ to some power, i.e. $f$ is an even polynomial).

Hence the four roots are of the form $\pm \alpha, \pm \beta$.

Note also that the splitting field $L$ of $f$ is $\mathbb F _ {p^4}$, since $[L : \mathbb F _ {p}] = \deg f(x) = 4$, and by general results the Galois group $G := \text{Gal}(L/\mathbb F _ {p}) = C _ 4$, and that $F$, the Frobenius endomorphism, generates $G$.

Also, $F(\alpha) = \pm \beta$, otherwise $F(\alpha) = -\alpha$ would have order $2$.

Now look at the roots. We know from the final coefficient of $f$ that

\[\alpha(-\alpha)\beta(-\beta) = \alpha^2 \beta^2 = 4\]

so $\alpha\beta = \pm 2 \pmod p$.

Then we may compute

\[F(\alpha \beta) = F(\pm 2) = \pm 2 = \alpha\beta = F(\alpha)F(\beta) = \pm \beta F(\beta) = \beta F(\pm \beta)\]

and thus $F(\pm \beta) = \alpha$. Thus $F^2 = \text{id}$, but this is a contradiction.

@example~ @exam~