Notes - Artificial Intelligence MT24, Nondeterministic search
Flashcards
@Define the difference between nondeterministic and stochastic.
Stochastic implies that the uncertainty about outcomes can be quantified in terms of probability.
A deterministic search problem can be formalised by:
- A set of states $S$
- An initial state $s$, where the agent starts
- Possible actions, described by a function $\mathbf{Actions}(s)$ which returns the set of actions applicable to state $s$
- A transition model, given by a successor function $\mathbf{Result}(s, a)$ which returns the state obtained by applying action $a$ to state $s$
- Goal test: A function for checking whether a state is a goal
- Path cost: A function assigning a value $\mathbf{pc}(p)$ to each path $p = s _ 0, a _ 1, s _ 1, a _ 2, \ldots$ and so on.
…and a solution is a sequence of states leading to a solution.
How does a nondeterministic environment change this model?
Rather than $\mathbf{Result}(s, a)$, it is $\mathbf{Results}(s, a)$, which returns a set of possible states. Now a solution is a contingency plan, like a game against nature.
Why is sensing needed in a nondeterministic environment?
You need to know the outcomes of your actions in order to know how to proceed according to your contingency plan.
Describe the And-Or @algorithm for search in nondeterministic algorithms, and describe its key differences with minimax (in the “game against nature” view).
- OR nodes: The agent has the choice of action (OuR choice)
- AND nodes: The environment chooses the action outcome (us AND THEM)
function AndOrGraphSearch(problem) return solution/failure:
# We get to make the first choice
return OrSearch(problem.InitialState, problem, [])
function OrSearch(state, problem, path) returns solution/failure:
# If we are making a choice, we just need to find one action that
# works.
if problem.GoalTest(state):
return empty plan
if state is on current path:
# There's a loop
return failure
for each action in problem.Actions(state):
# Otherwise, see if we can find a solution from by performing
# any of the actions
plan = AndSearch(results(state, action), problem, [state] + path)
if plan != failure:
return [action] + plan
return failure
function AndSearch(states, problem, path) return solution/failure:
# If nature is making the choice, we need to find a plan for every
# possible state nature puts us in.
for each s_i in states:
plan_i = OrSearch(s_i, problem, path)
# Even one possibility of failure means we're not guaranteed
# a solution.
if plan_i = failure:
return failure
return [
if s_1 then plan 1
...
else if s_{n-1} then plan n-1
else plan n
]
- Differences with minimax:
- Games against nature might last forever; in minimax if the opponent could force a cycle then this would be a draw. The algorithm can be modified to produce cyclic plans.
Is it true that every problem in a nondeterministic environment can be solved by an acyclic plan?
No.
Sometimes search in non-deterministic environments leads to plans which involve a cycle. In an adversarial environment, this would be bad news since the opponent could force a game to go on forever. But in the “game against nature” view of non-deterministic search, what’s sometimes a reasonable assumption to make?
The goal can be reached if each nondeterministic outcome occurs eventually.
Here’s a search tree generated by a few steps of And-Or search in the erratic vacuum world:
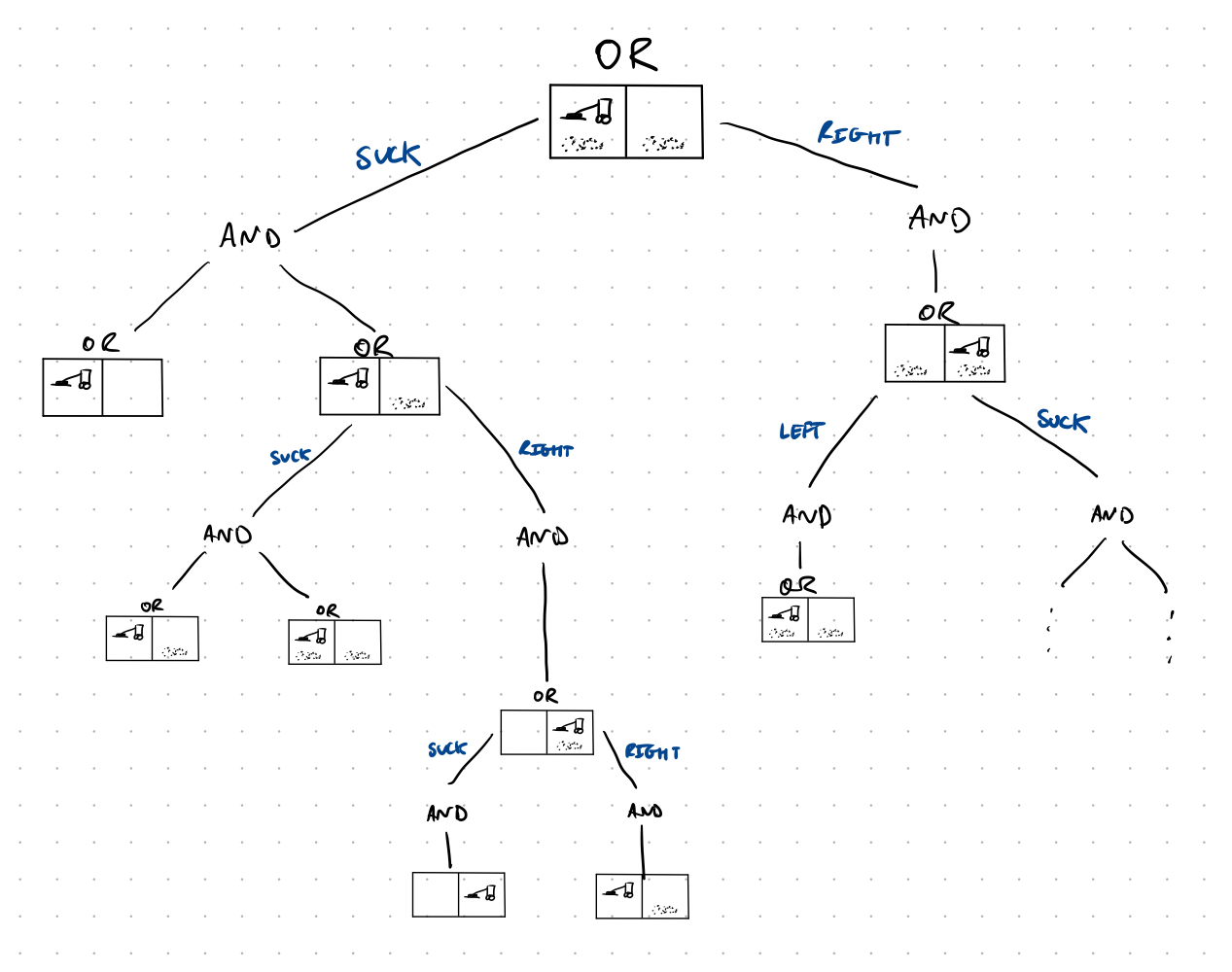
Here $\mathbf{Suck}$ applied to a dirty square will either clear one square or both, and $\mathbf{Suck}$ applied to a clean square might deposit dirt. Highlight the plan the algorithm would construct, and then write it down.
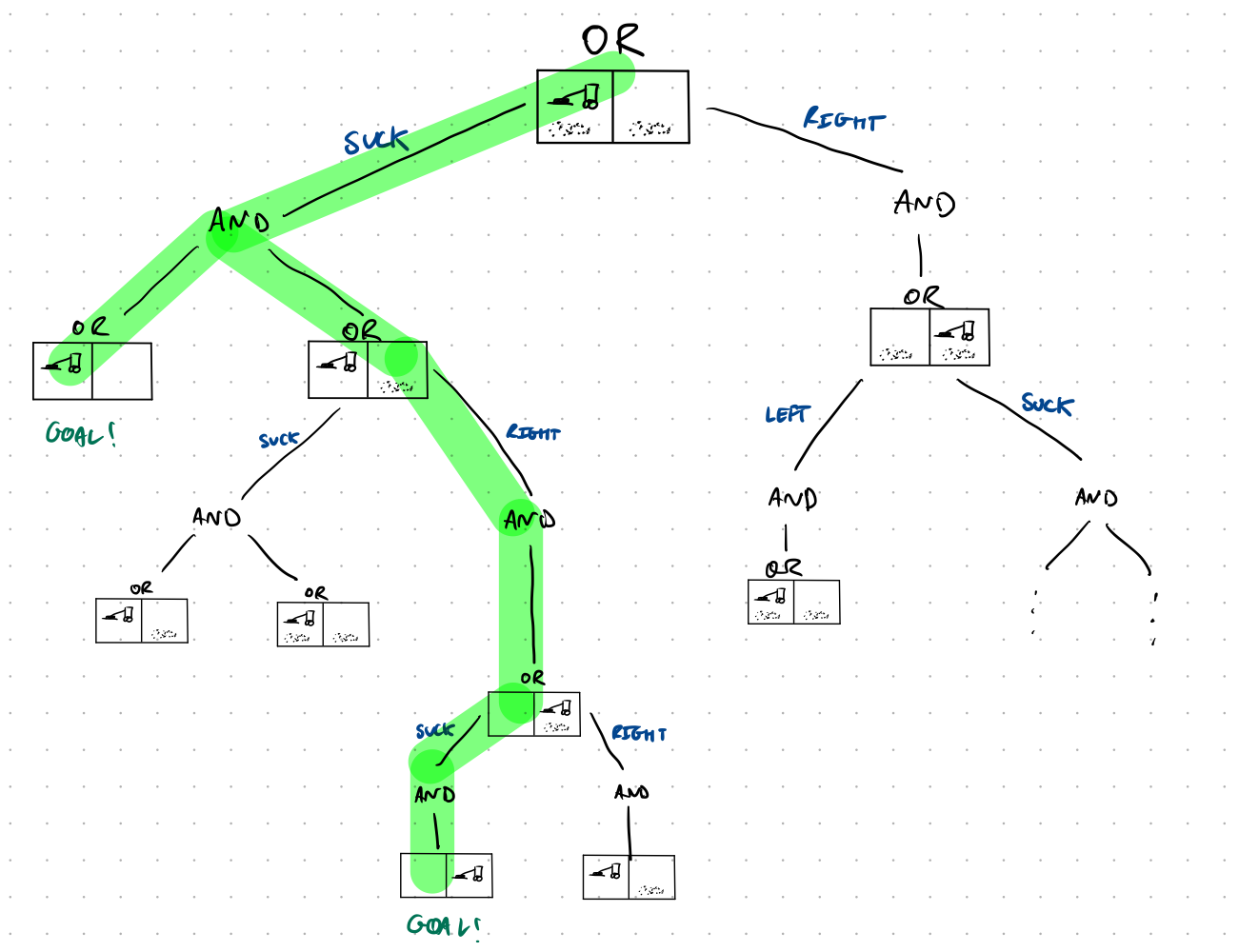
Using the notation L00, L01, L10, L11, R00, R01, R10, R11 for the 8 possible states, the plan would be:
[
Suck,
if L00 return [] else if L01 return [
Right,
if R01 return [
if R00 return []
]
]
]
@example~
And-Or search and belief state space
There is a lot of similarity between And-Or search and search through belief space. You could transform a search problem through belief space by instead performing And-Or search, and including each of the possible states as part of And nodes.
In this approach, the search tree would also begin with an And node.