Computer Vision MT25, Multiple view geometry
Flashcards
What are multi-view geometry problems?
Given cameras and correspondences, find a 3D reconstruction of a scene.
Epipolar geometry
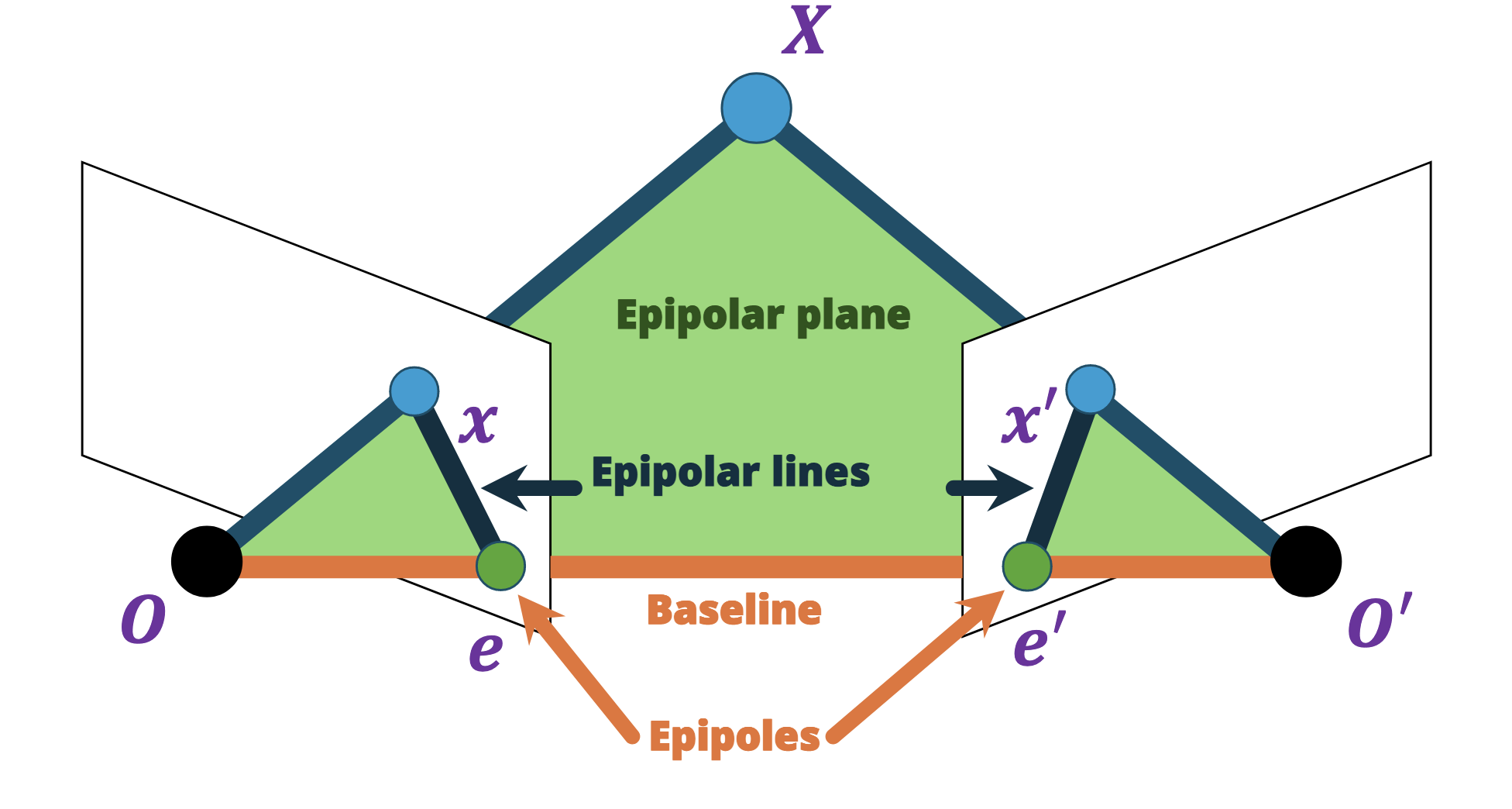
Suppose we have two cameras with centres $O$ and $O’$. @Define and @visualise the baseline.
The baseline is the line connecting the two origins.
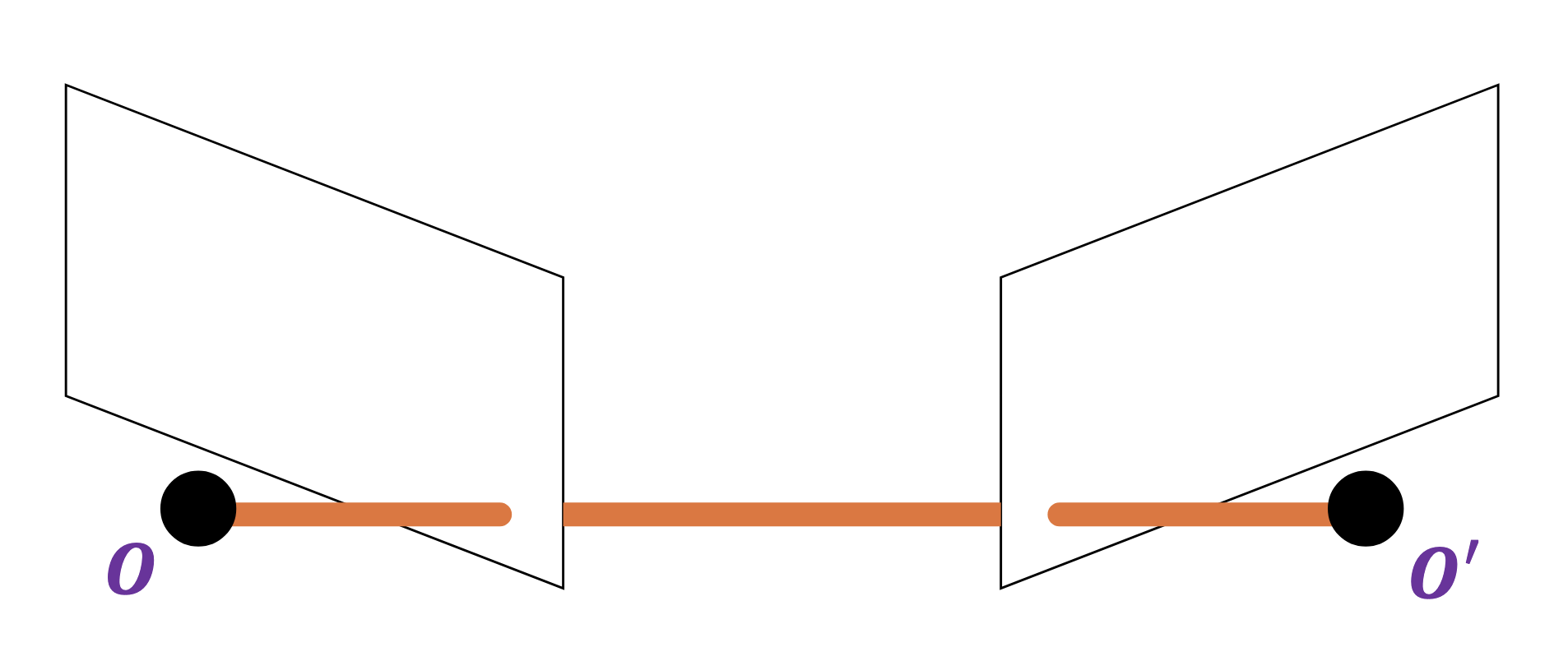
Suppose we have two cameras with centres $O$ and $O’$ connected by their baseline.

@Define and @visualise the epipoles $e$ and $e$’. What does this look like when the cameras lie on the same line?

The epipoles are where the baseline intersects with the image plane (equivalently, the projections of the other camera in each view).
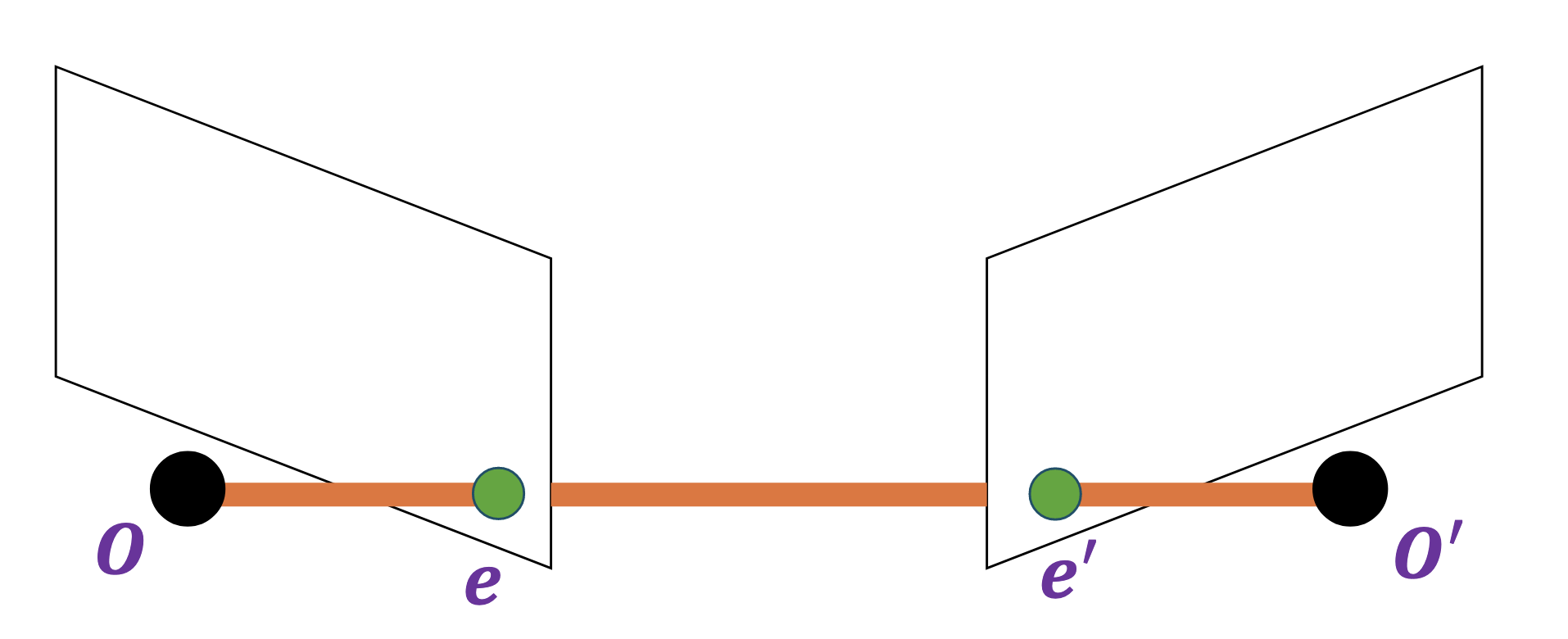
When the image planes lie on the same line, the epipoles are infinitely far away.
Suppose we have two cameras with centres $O$ and $O’$ with epipoles $e$ and $e’$, along with a point $X$ which projects onto $x$ and $x’$ respectively.
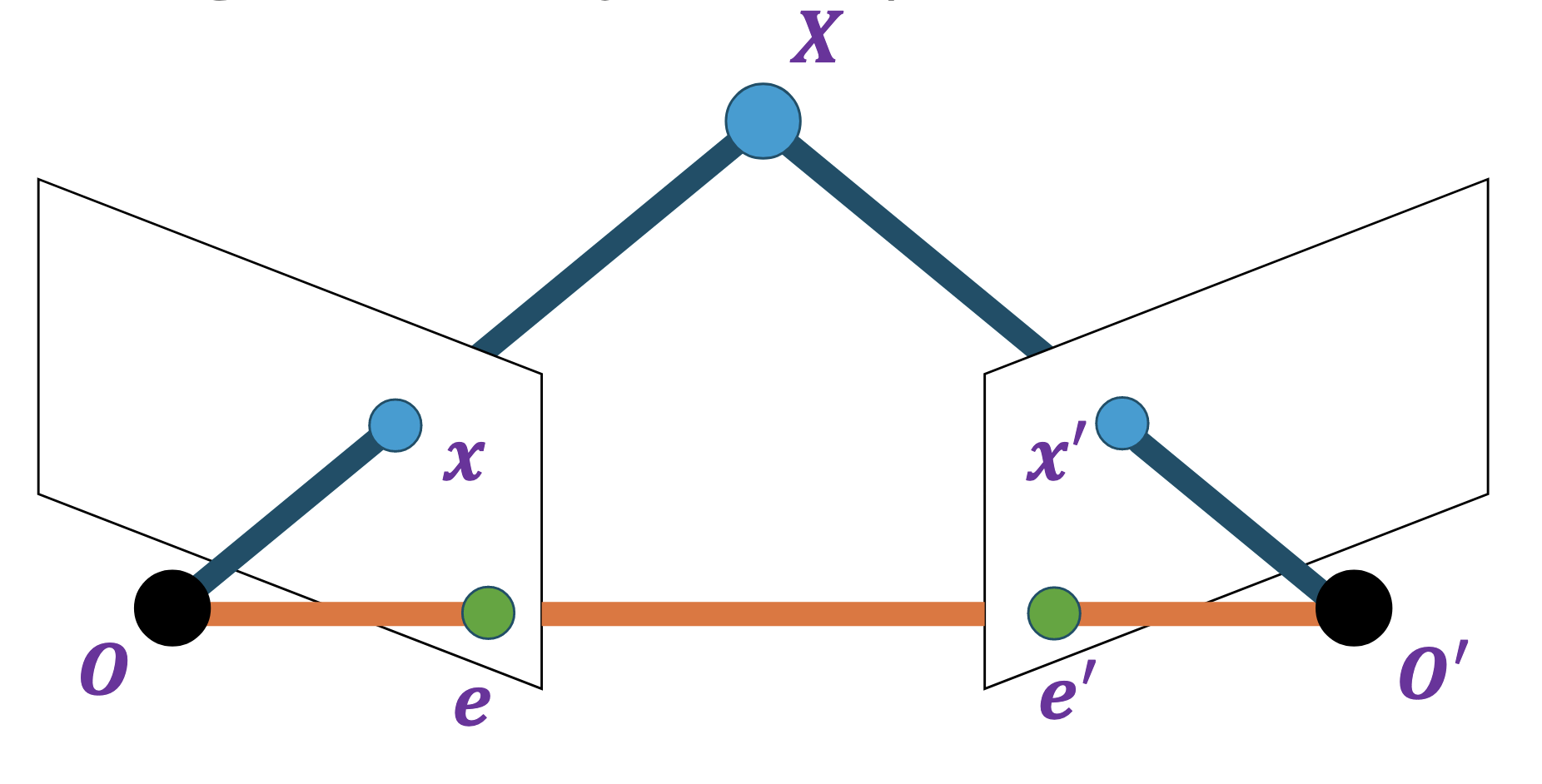
@Define and visualise the epipolar plane and the epipolar lines in this context.

- The epipolar plane is the plane formed by $X$, $O$ and $O’$.
- The epipolar lines connect the epipoles to the projections of $X$, or equivalently the intersection of the epipolar plane with the image plane.
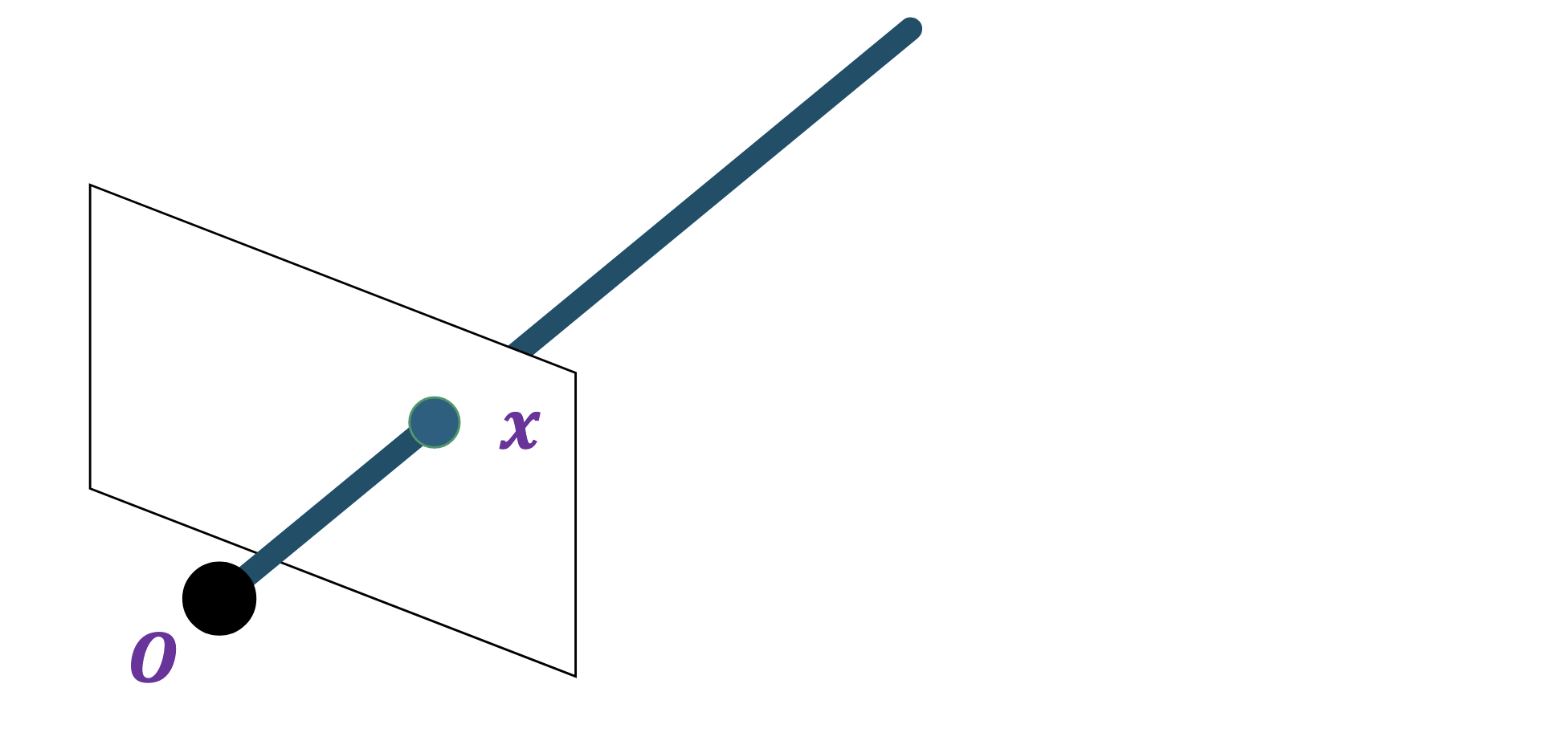
Suppose we observe a single point $x$ in some image taken by a camera with centre $O$.
Given another camera with centre $O’$, where can we find the $x’$ corresponding to the $x$ in the other image?

Along the epipolar line corresponding to $x$.
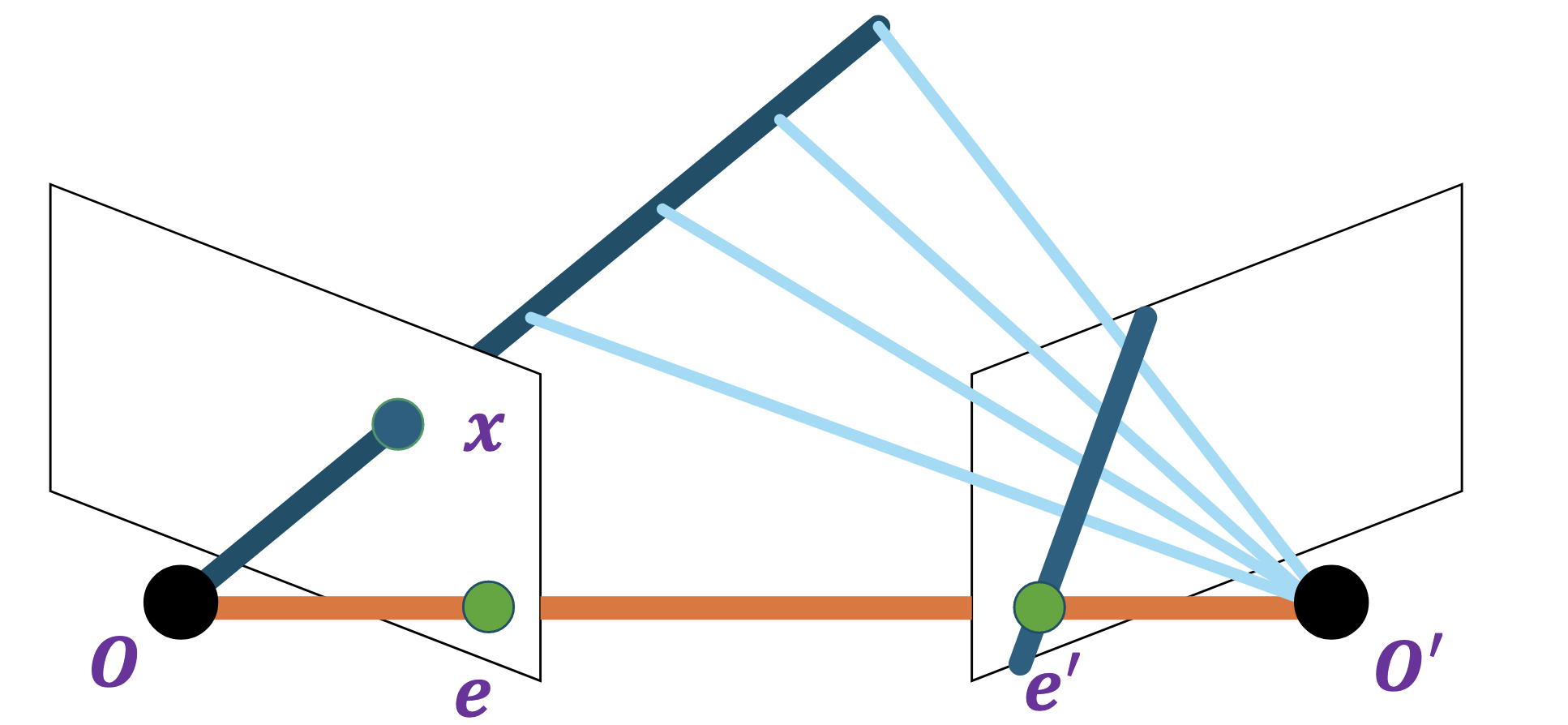
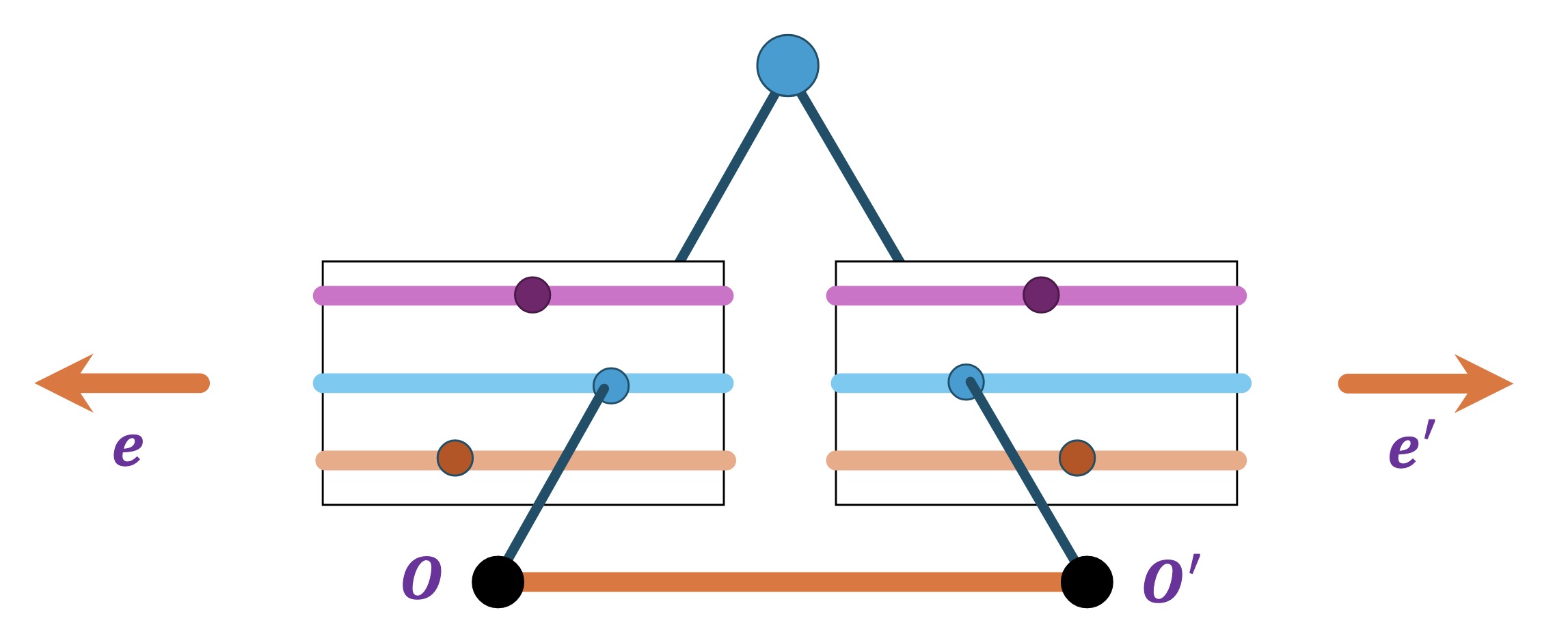
@Visualise what the epipolar lines would look like given a reference image and a target image.

@State and @visualise the epipolar constraint.
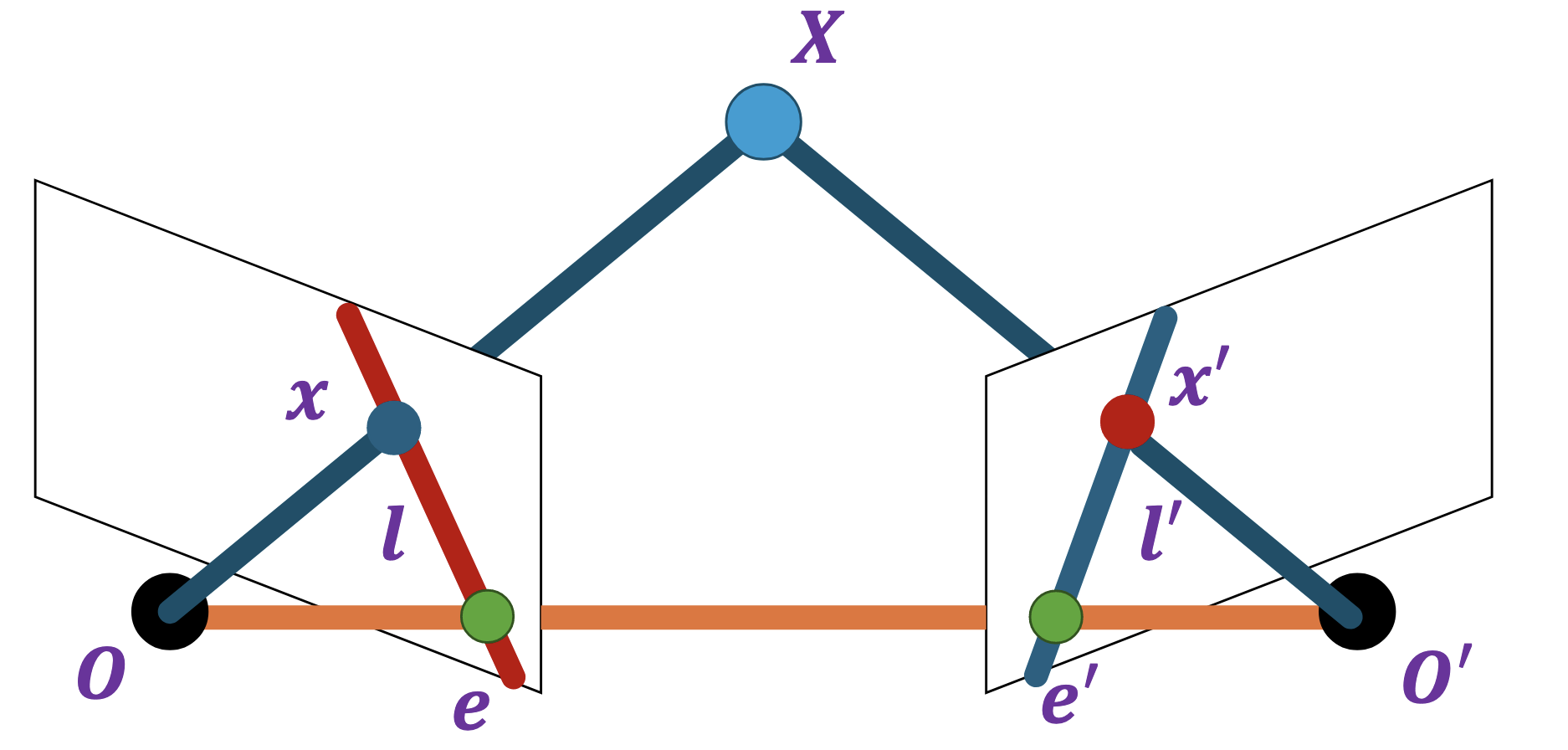
Whenever two points $x$ and $x’$ lie on matching epipolar lines $l$ and $l’$, the visual rays corresponding to them meet in space at some point $X$ (although they do not have to be projections of the same 3D point)
Consider the following setup:
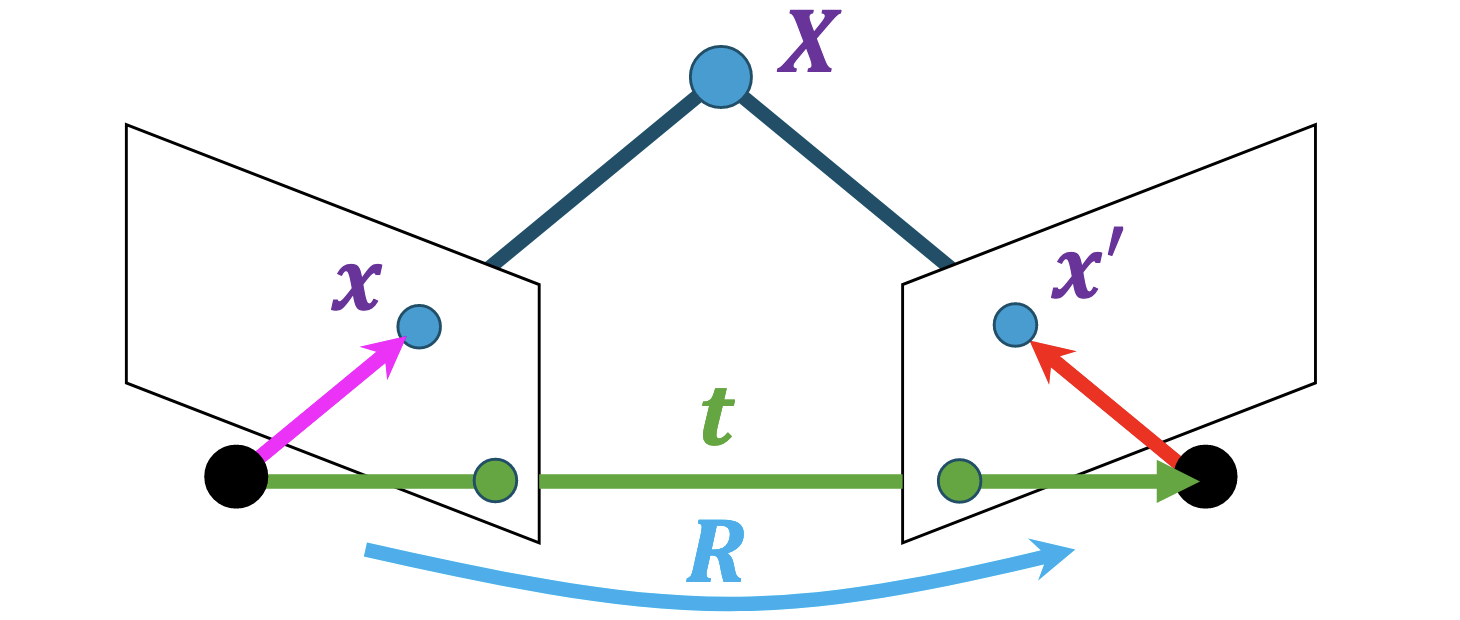
- We have two cameras at points $O$ and $O’$, of which the intrinsic $K, K’$ and extrinsic parameters are known
- The world coordinate system is set to that of the first camera
- The rotation and translation from $O$ to $O’$ is given as above
What are the two projection matrices $P, P’$ from the world coordinates to the camera coordinates?

- $K[I \mid 0]$
- $K’[R \mid t]$
Consider the following setup:

- We have two cameras at points $O$ and $O’$, of which the intrinsic $K, K’$ and extrinsic parameters are known
- The world coordinate system is set to that of the first camera
- The rotation and translation from $O$ to $O’$ is given as above, so that the projection matrices are given by $K[I \mid 0]$ and $K’[R \mid t]$
Given $X$, $x _ \text{pixel}$ and $x’ _ \text{pixel}$, where are $x$ and $x’$ in normalised image coordinates?

- $x _ \text{norm} = K^{-1} x _ \text{pixel} \cong [I \mid 0] X$
- $x’ _ \text{norm} = {K’}^{-1} x’ _ \text{pixel} \cong [R \mid t]X$
Consider the following setup:

- We have two cameras at points $O$ and $O’$, of which the intrinsic $K, K’$ and extrinsic parameters are known
- The world coordinate system is set to that of the first camera
- The rotation and translation from $O$ to $O’$ is given as above, so that the projection matrices are given by $K[I \mid 0]$ and $K’[R \mid t]$
- To simplify, we work in normalised image coordinates: given $X$, $x _ \text{pixel}$ and $x’ _ \text{pixel}$, we have
- $x _ \text{norm} = K^{-1} x _ \text{pixel} \cong [I \mid 0] X$
- $x’ _ \text{norm} = {K’}^{-1} x’ _ \text{pixel} \cong [R \mid t]X$
@State four different ways of expressing the relationship between $x$ and $x’$:
- By simply stating their exact relationship
- Using the cross product
- Using the “matrix form” of the cross product
- Using the essential matrix

- $x _ \text{norm} = K^{-1} x _ \text{pixel} \cong [I \mid 0] X$
- $x’ _ \text{norm} = {K’}^{-1} x’ _ \text{pixel} \cong [R \mid t]X$
Stating their exact relationship:
The direct transformation between $x$ and $x’$ gives
\[x' \cong Rx + t\]This means that $x’$, $Rx$ and $t$ are linearly dependent, so:
Using the cross product:
\[x' \cdot [t \times (Rx)] = 0\]Since
\[a \times b = \begin{bmatrix} 0 & -a _ 3 & a _ 2 \\ a _ 3 & 0 & -a _ 1 \\ -a _ 2 & a _ 1 & 0 \end{bmatrix} \begin{pmatrix} b _ 1 \\ b _ 2 \\ b _ 3 \end{pmatrix} := [a _ \times] b\]we have:
Using the “matrix form” of the cross product:
\[x'^\top [t _ \times] Rx = 0\]so defining $[t _ x] R = E$ as the “essential matrix”:
Using the essential matrix:
\[x'^\top E x = 0\]Consider the following setup:

- We have two cameras at points $O$ and $O’$, of which the intrinsic $K, K’$ and extrinsic parameters are known
- The world coordinate system is set to that of the first camera
- The rotation and translation from $O$ to $O’$ is given as above, so that the projection matrices are given by $K[I \mid 0]$ and $K’[R \mid t]$
- To simplify, we work in normalised image coordinates: given $X$, $x _ \text{pixel}$ and $x’ _ \text{pixel}$, we have
- $x _ \text{norm} = K^{-1} x _ \text{pixel} \cong [I \mid 0] X$
- $x’ _ \text{norm} = {K’}^{-1} x’ _ \text{pixel} \cong [R \mid t]X$
Then the direct transformation between $x$ and $x’$ gives
\[x' \cong Rx + t\]
this means that $x’$, $Rx$ and $t$ are linearly dependent, so we have
\[x' \cdot [t \times (Rx)] = 0\]
Collecting this into matrix form and defining $[t _ x] R = E$ as the “essential matrix”, we have
\[x'^\top E x = 0\]
@State how you may:
- Determine the epipolar line $l’$ corresponding to a point $x$
- Determine the epipolar line $l$ corresponding to a point $x’$

- $x _ \text{norm} = K^{-1} x _ \text{pixel} \cong [I \mid 0] X$
- $x’ _ \text{norm} = {K’}^{-1} x’ _ \text{pixel} \cong [R \mid t]X$
- $l’ = Ex$
- $l = E^\top x’$
Consider the following setup:

- We have two cameras at points $O$ and $O’$, of which the intrinsic $K, K’$ and extrinsic parameters are known
- The world coordinate system is set to that of the first camera
- The rotation and translation from $O$ to $O’$ is given as above, so that the projection matrices are given by $K[I \mid 0]$ and $K’[R \mid t]$
- To simplify, we work in normalised image coordinates: given $X$, $x _ \text{pixel}$ and $x’ _ \text{pixel}$, we have
- $x _ \text{norm} = K^{-1} x _ \text{pixel} \cong [I \mid 0] X$
- $x’ _ \text{norm} = {K’}^{-1} x’ _ \text{pixel} \cong [R \mid t]X$
Then the direct transformation between $x$ and $x’$ gives
\[x' \cong Rx + t\]
this means that $x’$, $Rx$ and $t$ are linearly dependent, so we have
\[x' \cdot [t \times (Rx)] = 0\]
Collecting this into matrix form and defining $[t _ x] R = E$ as the “essential matrix”, we have
\[x'^\top E x = 0\]
@State the relationship between the essential matrix $E$ and the epipolar points $e$ and $e’$.

- $x _ \text{norm} = K^{-1} x _ \text{pixel} \cong [I \mid 0] X$
- $x’ _ \text{norm} = {K’}^{-1} x’ _ \text{pixel} \cong [R \mid t]X$
- $Ee = 0$
- $E^\top e’ = 0$
Consider the following setup:

- We have two cameras at points $O$ and $O’$, of which the intrinsic $K, K’$ and extrinsic parameters are known
- The world coordinate system is set to that of the first camera
- The rotation and translation from $O$ to $O’$ is given as above, so that the projection matrices are given by $K[I \mid 0]$ and $K’[R \mid t]$
- To simplify, we work in normalised image coordinates: given $X$, $x _ \text{pixel}$ and $x’ _ \text{pixel}$, we have
- $x _ \text{norm} = K^{-1} x _ \text{pixel} \cong [I \mid 0] X$
- $x’ _ \text{norm} = {K’}^{-1} x’ _ \text{pixel} \cong [R \mid t]X$
Then the direct transformation between $x$ and $x’$ gives
\[x' \cong Rx + t\]
this means that $x’$, $Rx$ and $t$ are linearly dependent, so we have
\[x' \cdot [t \times (Rx)] = 0\]
Collecting this into matrix form and defining $[t _ x] R = E$ as the “essential matrix”, we have
\[x'^\top E x = 0\]
What assumptions do we drop in order to @define the fundamental matrix?

- $x _ \text{norm} = K^{-1} x _ \text{pixel} \cong [I \mid 0] X$
- $x’ _ \text{norm} = {K’}^{-1} x’ _ \text{pixel} \cong [R \mid t]X$
- We assume that the calibration matrices $K$ and $K’$ of the two cameras are unknown
- This gives $x’^\top F x = 0$ where $F = (K’^{-1})^\top E K^{-1}$
Consider the following setup:

- We have two cameras at points $O$ and $O’$, of which the intrinsic $K, K’$ and extrinsic parameters are known
- The world coordinate system is set to that of the first camera
- The rotation and translation from $O$ to $O’$ is given as above, so that the projection matrices are given by $K[I \mid 0]$ and $K’[R \mid t]$
- To simplify, we work in normalised image coordinates: given $X$, $x _ \text{pixel}$ and $x’ _ \text{pixel}$, we have
- $x _ \text{norm} = K^{-1} x _ \text{pixel} \cong [I \mid 0] X$
- $x’ _ \text{norm} = {K’}^{-1} x’ _ \text{pixel} \cong [R \mid t]X$
Then the direct transformation between $x$ and $x’$ gives
\[x' \cong Rx + t\]
this means that $x’$, $Rx$ and $t$ are linearly dependent, so we have
\[x' \cdot [t \times (Rx)] = 0\]
Collecting this into matrix form and defining $[t _ x] R = E$ as the “essential matrix”, we have
\[x'^\top E x = 0\]
For the fundamental matrix, we drop some assumptions:
- We assume that the calibration matrices $K$ and $K’$ of the two cameras are unknown
- This gives $x’^\top F x = 0$ where $F = (K’^{-1})^\top E K^{-1}$
@State:
- The relationship between the essential matrix $E$ and the epipolar points $e$ and $e’$.
- How you would determine the epipolar line $l’$ corresponding to a point $x$
- How you would determine the epipolar line $l$ corresponding to a point $x’$

- $x _ \text{norm} = K^{-1} x _ \text{pixel} \cong [I \mid 0] X$
- $x’ _ \text{norm} = {K’}^{-1} x’ _ \text{pixel} \cong [R \mid t]X$
- $l’ = Fx$
- $l = F^\top x$
- $Fe = 0$
- $F^\top e’ = 0$
Given that the fundamental matrix satisfies the equation
\[x'^\top F x = 0\]
Derive the eight-point algorithm for determining an estimate of $F$.
Explicitly, we require for each pair of points $\pmb x, \pmb x’$
\[\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix}^\top \begin{bmatrix} f _ {11} & f _ {12} & f _ {13} \\ f _ {21} & f _ {22} & f _ {23} \\ f _ {31} & f _ {32} & f _ {33} \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = 0\]which, vectorising $f$ gives
\[\begin{pmatrix} x'x & x'y & x' &y'x & y'y & y' & x & 1 \end{pmatrix} \begin{pmatrix} f _ {11} \\ f _ {12} \\ f _ {13} \\ f _ {21} \\ f _ {22} \\ f _ {23} \\ f _ {31} \\ f _ {32} \\ f _ {33} \\ \end{pmatrix} = 0\]Collecting this into a matrix equation for each of the point correspondences, we have
\[Uf = 0\]where
\[\begin{aligned} U &= \begin{pmatrix} x _ 1'x _ 1 & x _ 1'y _ 1 & x _ 1' &y _ 1'x _ 1 & y _ 1'y _ 1 & y _ 1' & x _ 1 & 1 \\ & & & \vdots & & & & \\ x _ n'x _ n & x _ n'y _ n & x _ n' &y _ n'x _ n & y _ n'y _ n & y _ n' & x _ n & n \\ \end{pmatrix} \\ \\ \end{aligned}\]which can be solved via least squares. To enforce the fact $F$ must be rank $2$, we can take the best rank-2 approximation of the found solution using truncated SVD.