Galois Theory HT25, Main theorems of Galois theory
-
The main observations of Galois theory
- There is a bijective correspondence between subgroups and subfields
- Galois intermediate subfields correspond to normal subgroups of $G$, and the quotient groups are nice
- The correspondences are inclusion reversing
- The indexes of the intermediate fields correspond to the indexes of the quotient groups
- Flashcards
The main observations of Galois theory
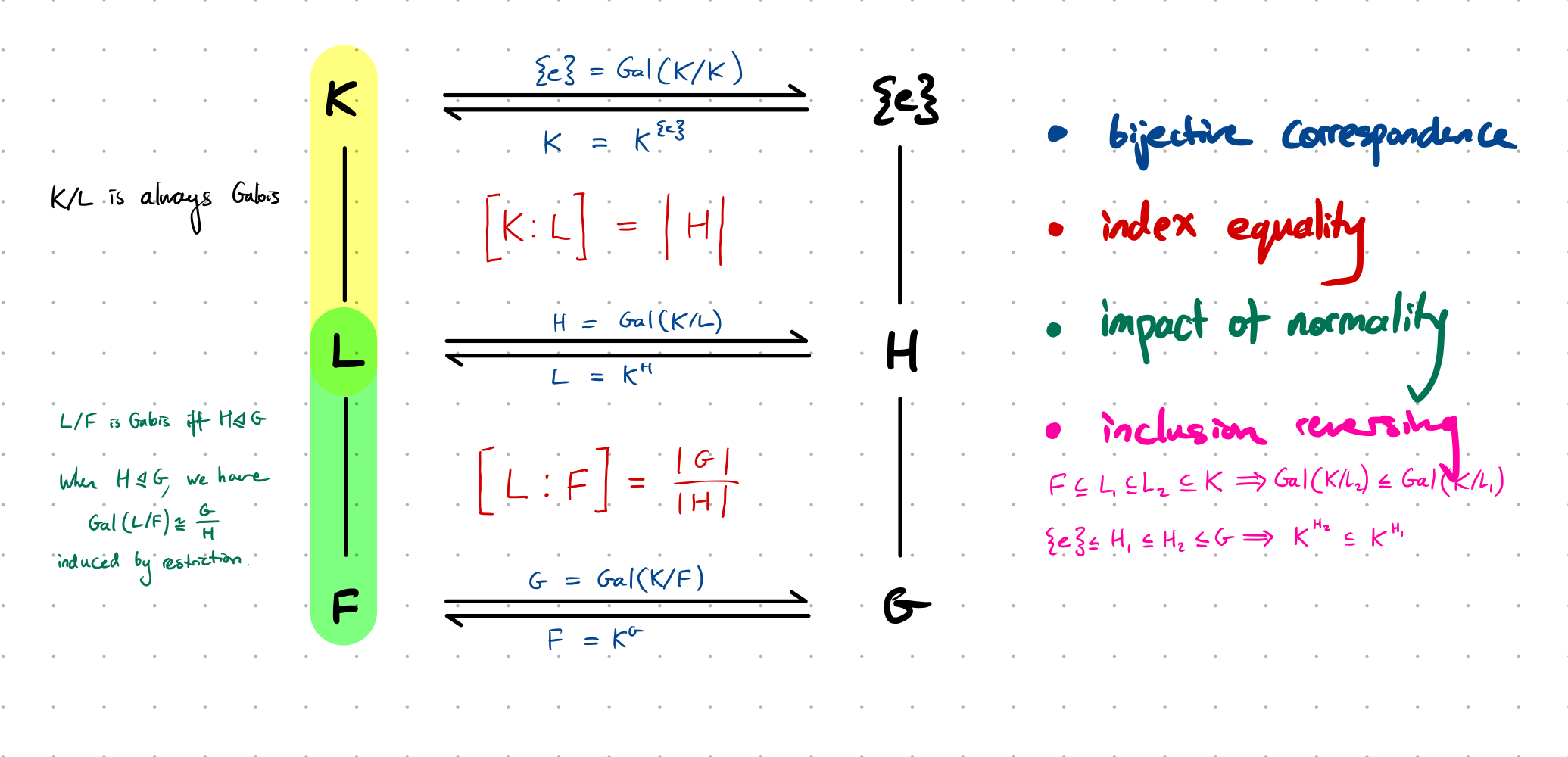
Let $K/F$ be aGalois extension, and let $L$ be some intermediate field. The main observations of Galois theory are as follows.
There is a bijective correspondence between subgroups and subfields
The function $L \mapsto \text{Gal}(K/L)$ is a bijection with inverse $H \mapsto K^H$, and establishes a correspondence between the intermediate fields $F \subseteq L \subseteq K$ and the subgroups of $H \le \text{Gal}(K/F)$.
Proof overview
Let $f(L) := \text{Gal}(K/L)$ and $g(H) := K^H$. We want to show that $f$ and $g$ are mutual inverses, so that $f$ and $g$ are bijections.
To see $g(f(L)) = L$, i.e. that $f$ is injective:
- $K/L$ is Galois (proof).
- Therefore $K^{\text{Gal}(K/L)} = L$ by the result which says that an extension $K/L$ being Galois is equivalent to $K^G = L$ where $G = \text{Gal}(K/L)$ (proof).
Some materials in fact define a Galois extension to be one such that $K^G = F$, in which case step (2) is not needed.
To see $f(g(H)) = H$, i.e. that $f$ is surjective:
- We have a result that says if $H \le \text{Gal}(K/F)$, then $\text{Gal}(K/K^H) = H$. (proof).
- Since $f(g(H)) = \text{Gal}(K/K^H)$ (by definition), the result follows.
- Alternatively, $\text{Gal}(K/K^H) = H$ follows from [[Notes - Galois Theory HT25, Artin’s lemma]]U applied to $K$ and $H$.
Galois intermediate subfields correspond to normal subgroups of $G$, and the quotient groups are nice
- Intermediate subfields $F \subseteq L \subseteq K$ that are Galois over $F$ correspond precisely with the normal subgroups $H$ of $G$ under the above mapping
- For any Galois extension $L/F$ we have:
Proof overview
This is full proof ishere. For (1), one proof proceeds roughly as follows:
- $H$ is normal in $G$
- $\iff$ $K^H$ is $G$-stable (proof)
- $\iff$ $L$ is $G$-stable (by the first theorem, $K^H = L$ if $H = \text{Gal}(K/L))$
- $\iff$ $L/F$ is Galois (proof)
For (2), we have
- $H$ is normal in $G$
- $\implies$ $L$ is Galois over $F$ (by the above)
- $\implies$ $L$ is $G$-stable (by the above)
- $\implies$ $r : G \to \text{Gal}(L/F)$ is a well-defined surjective group homomorphism (proof, can also use Artin’s lemma)
- $\implies G/(\ker r) = G/H \cong \text{Gal}(L/F)$ by the first-isomorphism theorem
The correspondences are inclusion reversing
If $F \subseteq L _ 1 \subseteq L _ 2 \subseteq K$, then $\text{Gal}(K/L _ 2) \le \text{Gal}(K/L _ 1)$, and if $H _ 1 \le H _ 2 \le G$, then $K^{H _ 2} \subseteq K^{H _ 1}$.
Proof overview
The most straightforward of all the claims of the main theorem.
- If $F \subseteq L _ 1 \subseteq L _ 2 \subseteq K$, then every $L _ 2$-linear automorphism of $K$ is also a $L _ 1$-linear automorphism of $K$. Thus $\text{Gal}(K/L _ 2) \le \text{Gal}(K/L _ 1)$.
- If $H _ 1 \le H _ 2 \le G$, then if some $k \in K$ is fixed by every $h \in H _ 2$, then it is also fixed by every $h \in H _ 1$, so $K^{H _ 2} \subseteq K^{H _ 1}$.
The indexes of the intermediate fields correspond to the indexes of the quotient groups
If $F \subseteq L \subseteq K$ is an intermediate field and $H = \text{Gal}(K/L)$, then
\[[L : F] = |G/H|\]and
\[[K : L] = |H|\]Proof overview
We know that for every Galois extension $K/F$, $[K : F] = \vert G \vert $ (proof), and likewise as $K/L$ is Galois (proof), $[K : L] = \vert H \vert $. But then by the Tower Law and properties of group quotients:
\[[L : F] = \frac{[K : F]}{[K : L]} = \frac{|G|}{|H|} = |G/H|\]Flashcards
Main statement
Suppose:
- $K/F$ is a Galois extension
- $G = \text{Gal}(K/F)$
@State the results that together comprise the main observations of Galois theory.

Bijective correspondence of subgroups and subfields:
The function $L \mapsto \text{Gal}(K/L)$ is a bijection with inverse $H \mapsto K^H$, and establishes a correspondence between the intermediate fields $F \subseteq L \subseteq K$ and the subgroups of $H \le \text{Gal}(K/F)$.
The intermediate subfields which are Galois correspond to the normal subgroups of $G$:
Intermediate subfields $F \subseteq L \subseteq K$ that are Galois over $F$ correspond precisely with the normal subgroups $H$ of $G$ under the above mapping, and for any Galois extension $L/F$ we have:
\[\text{Gal}(L/F) \cong \frac{\text{Gal}(K/F)}{\text{Gal}(K/L)}\]The correspondences are inclusion reversing:
If $F \subseteq L _ 1 \subseteq L _ 2 \subseteq K$, then $\text{Gal}(K/L _ 2) \le \text{Gal}(K/L _ 1)$, and if $H _ 1 \le H _ 2 \le G$, then $K^{H _ 2} \subseteq K^{H _ 1}$.
The indexes of the intermediate fields correspond to the indexes of the quotient groups:
If $F \subseteq L \subseteq K$ is an intermediate field and $H = \text{Gal}(K/L)$, then
\[[L : F] = |G/H|\]and
\[[K : L] = |H|\]$K/F$ is Galois and $K/L/F$, then $K/L$ is Galois
Suppose:
- $K/F$ is a Galois extension
- $F \subseteq L \subseteq K$
@State what you can then conclude about $K/L$.
$K/L$ is also Galois.
@Justify that if:
- $K/F$ is a Galois extension
- $F \subseteq L \subseteq K$
Then:
- $K/L$ is also Galois.
- Since $K/F$ is Galois, by definition $K$ is a splitting field for some separable polynomial $f \in F[t]$.
- As the roots of $f$ in $K$ still generate $K$ as a field and $f$ is still separable when viewed as an element of $L[t]$ (this follows from previous results), $K/L$ is also Galois.
@important~ (main theorem)
$K/F$ is Galois and $K/L/F$, then $L=K^{\text{Gal}(K/L)}$
Suppose:
- $K/F$ is a Galois extension
- $L$ in $F \subseteq L \subseteq K$ is an intermediate field
@State a result that relates $L$ to a fixed field.
Suppose:
- $K/F$ is a Galois extension
- $L$ in $F \subseteq L \subseteq K$ is an intermediate field
@Prove that
\[L = K^{\text{Gal}(K/L)}\]
This comes from two previous results:
If:
- $K/F$ is a Galois extension
- $F \subseteq L \subseteq K$
Then:
- $K/L$ is also Galois.
and
If:
- $K/F$ is a finite extension
- $G = \text{Gal}(K/F)$
Then the following are equivalent:
- $K/F$ is Galois.
- $ \vert G \vert = [K : F]$
- $F = K^G$
In the above, $K/L$ is also Galois. But then $L = K^{\text{Gal}(K/L)}$.
$K/F$ is Galois, then the normal subgroups $H \trianglelefteq \text{Gal}(K/F)$ correspond to Galois extensions $L / F$
Suppose:
- $K$ is a field
- $H$ is a finite group of automorphisms of $K$
- $z \in K$
@Prove that:
- $z$ is algebraic over $K^H$
- $m _ {K^H, z} = f _ {H \cdot z}$
- $\deg m _ {K^H, z} = \vert H \cdot z \vert $.
1: Consider the polynomial $f _ {H \cdot z}$ defined by
\[f _ {H \cdot z}(t) := \prod _ {y \in H \cdot z} (t - y)\]Since $f _ {H \cdot z}(z) = 0$ and $f _ {H \cdot z}$ has coefficients in $K^H$ (by previous results), it follows $z$ is algebraic over $K^H$.
2: Since $f _ {H \cdot z}(z) = 0$, $m _ {K^H, z}$ must divides $f _ {H \cdot z}$.
But also, $K \le \text{Gal}(K/K^H)$, so $H$ acts on the roots of $m _ {K^H, z}$ in $K$. Since $z$ is a root of $m _ {K^H, z}$ in $K$, it follows that the entire $H$-orbit $H\cdot z$ is contained in the set of roots of $m _ {K^H, z}$. Hence $f _ {H \cdot z} \mid m _ {K^H, z}$.
Since both $f _ {H \cdot z}$ and $m _ {K^H, z}$ are monic, there must be equality.
3. This follows from 2.
Suppose:
- $K/F$ is a Galois extension
- $H \le \text{Gal}(K/F)$
@State a result that establishes one direction of the Galois correspondence works in this case.
Suppose:
- $K/F$ is a Galois extension
- $H \le \text{Gal}(K/F)$
@Prove that
\[\text{Gal}(K/K^H) = H\]
Let $J := \text{Gal}(K/K^H)$. This is a finite group since $K/K^H$ is a finite extension and $H \le J$, since almost tautologically
\[\begin{aligned} \varphi \in H &\implies \varphi \text{ is a }K^H\text{-linear aut. of }K \\\\ &\implies \varphi \in \text{Gal}(K/K^H) = J \end{aligned}\]We aim to show that $ \vert H \vert = \vert J \vert $, since this together with $H \le J$ implies $H = J$.
Choose some $k \in K$ such that $\text{Stab} _ J(z) = \lbrace\text{id}\rbrace$, this is always possible by previous results (lower bounds on the size of Galois groups). Then by the orbit-stabiliser theorem,
\[|H| = |H\cdot z| \cdot |\lbrace \text{id}\rbrace| = \deg m _ {K^H, z}\]and
\[|J| = |J \cdot z| \cdot |\lbrace \text{id}\rbrace| = \deg m _ {K^J, z}\]Hence it is enough to show that $K^J = K^H$, since then these polynomials will be the same and $ \vert H \vert = \vert J \vert $. Since $K/F$ is a Galois extension, the extension $K/K^H$ is also Galois with Galois group $\text{Gal}(K/K^H) = J$. By the result that says
If:
- $K/F$ is a finite extension
- $G = \text{Gal}(K/F)$
Then the following are equivalent:
- $K/F$ is Galois.
- $ \vert G \vert = [K : F]$
- $F = K^G$
It then follows that $K^J = K^H$.
@important~ (main theorem)
Suppose:
- $K/F$ is a Galois extension
- $L$ is an intermediate field
- $L$ is $\text{Gal}(K/F)$-stable
@State a result that gives you a relationship between $\text{Gal}(K/F)$ and $\text{Gal}(L/F)$.
The restriction map
\[r : \text{Gal}(K/F) \to \text{Gal}(L/F)\]is a well-defined surjective group homomorphism.
Suppose:
- $K/F$ is a Galois extension
- $L$ is an intermediate field
- $L$ is $\text{Gal}(K/F)$-stable
@Prove that the restriction map
\[r : \text{Gal}(K/F) \to \text{Gal}(L/F)\]
is a well-defined surjective group homomorphism.
- Well-defined: If $\sigma \in \text{Gal}(K/F)$, then $r(\sigma) = \sigma \vert _ L : L \to K$ is an element of $\text{Gal}(L/F)$ since $L$ is $\text{Gal}(K/F)$-stable.
- Group homomorphism: This is by construction.
- Surjective: Any $F$-stable automorphism of $L$ extends to an automorphism of $K$ by the theorem:
Suppose:
- $\varphi : F \to \tilde F$ is an isomorphism of fields
- $f \in F[t]$ is a separable polynomial
- $K$ is a splitting field for $f$
- $\tilde f = \varphi(f)$
- $\tilde K$ is a splitting field for $\tilde f$
Then there are at least $[K : F]$ distinct isomorphisms extending $\varphi$ to an isomorphism $\phi’ : K \to \tilde K$.
Suppose:
- $K/F$ is a Galois extension
- $G = \text{Gal}(K/F)$
- $L$ is an intermediate field $F \subseteq L \subseteq K$
@State two exact characterisations of when $L/F$ is Galois.
- $L/F$ is Galois iff $L$ is $G$-stable.
- $L/F$ is Galois iff $\text{Gal}(K/L) \trianglelefteq G$
@Prove that if
- $K/F$ is a Galois extension
- $G = \text{Gal}(K/F)$
- $L$ is an intermediate field $F \subseteq L \subseteq K$
then $L/F$ is Galois if and only if $L$ is $G$-stable.
Forward direction: Suppose $L/F$ is Galois. Then it is a splitting field of a separable polynomial $g \in F[t]$, so the roots $V(g)$ of $g$ in $L$ generate $L$. But $V(g)$ is $G$-stable, and so $L$ is also $G$-stable.
Backward direction: Suppose that $L$ is $G$-stable. Then by the result that says
If:
- $K/F$ is a finite extension
- $G = \text{Gal}(K/F)$
Then the following are equivalent:
- $K/F$ is Galois.
- $ \vert G \vert = [K : F]$
- $F = K^G$
it is enough to show that $L^{\text{Gal}(L/F)} = F$. Recall also the result that:
\[r : \text{Gal}(K/F) \to \text{Gal}(L/F)\]If
- $K/F$ is a Galois extension
- $L$ is an intermediate field
- $L$ is $\text{Gal}(K/F)$-stable
Then the restriction map
is a well-defined surjective group homomorphism.
Hence $r(G) \le \text{Gal}(L/F)$. But then
\[\begin{aligned} L^{\text{Gal}(L/F)} &\subseteq L^{r(G)} &&(\text{since } r(G) \le \text{Gal}(L/F)) \\\\ &= \lbrace x \in L \mid \tau(x) = x \text{ for all } \tau \in r(G) \rbrace \\\\ &= \lbrace x \in L \mid \sigma(x) = x \text{ for all } \sigma \in G \rbrace && (\tau(x) = x \iff \sigma(x) = x \text { when }x \in L) \\\\ &= L \cap \lbrace x \in K \mid \sigma(x) = x \text{ for all } \sigma \in G \rbrace \\\\ &= L \cap K^G \\\\ &= L \cap F &&(G\text{ is Galois}) \\\\ &= F \end{aligned}\]Suppose:
- $K/F$ is a Galois extension
- $G = \text{Gal}(K/F)$
- $H \le G$
- $\varphi \in G$
@State a relationship between $K$, $H$ and $\varphi$.
Suppose:
- $K/F$ is a Galois extension
- $G = \text{Gal}(K/F)$
- $H \le G$
- $\varphi \in G$
@Justify that then
\[K^{\varphi H \varphi^{-1} } = \varphi(K^H)\]
Let $x \in K$ and $\psi \in H$. Then $(\varphi \psi \varphi^{-1}) \cdot x = x$ iff $\psi(\varphi^{-1} x) = \varphi^{-1}x$. So $x \in K^{\varphi H \varphi^{-1} } \iff \varphi^{-1}(x) \in K^H \iff x \in \varphi(K^H)$.
Suppose:
- $K/F$ is a Galois extension
- $G = \text{Gal}(K/F)$
- $L$ is an intermediate subfield
- $H := \text{Gal}(K/L)$
@State a result about what the normality of $H$ tells you about the field.
$H$ is normal in $G$ iff $L$ is Galois over $F$.
Suppose:
- $K/F$ is a Galois extension
- $L$ is an intermediate subfield
- $G = \text{Gal}(K/F)$
- $H := \text{Gal}(K/L)$
- $H$ is a normal subgroup of $G$
One consequence of this is that $K/L$ is Galois (in fact, this is an if and only if).
@State another result about the quotient $G/H$ in this case.
- The restriction map $\text{Gal}(K/F) \to \text{Gal}(L/F)$ induces a group isomorphism $G/H \cong \text{Gal}(L/F)$.
Suppose:
- $K/F$ is a Galois extension
- $G = \text{Gal}(K/F)$
- $L$ is an intermediate subfield
- $H := \text{Gal}(K/L)$
@Prove that then:
- $H$ is normal in $G$ iff $L$ is Galois over $F$.
- If $H$ is normal in $G$, the restriction map $\text{Gal}(K/F) \to \text{Gal}(L/F)$ induces a group isomorphism $G/H \cong \text{Gal}(L/F)$.
(1):
\[\begin{align} H \trianglelefteq G &\iff \varphi H \varphi^{-1} = H \text{ for all } \varphi \in G \\\\ &\iff K^{\varphi H \varphi^{-1} } = K^H \text{ for all } \varphi \in G && \\\\ &\iff \varphi(K^H) = K^H \text{ for all }\varphi \in G && (1\star)\\\\ &\iff K^H \text{ is }G\text{-stable} \\\\ &\iff K^H / F \text{ is Galois} &&(2\star) \\\\ &\iff L/F \text{ is Galois} &&(3\star) \end{align}\]where:
- $(1\star)$ is justified by the general result that $K^{\varphi H \varphi^{-1} } = \varphi(K^H)$.
- $(2\star)$ is justified by the result that says if $K/F$ is a Galois extension with $G = \text{Gal}(K/F)$ and $L$ is an intermediate field, then $L/F$ is Galois iff $L$ is $G$-stable
- $(3\star)$ is justified by one of the main theorems of Galois theory; namely that if $K/F$ is a Galois extension and $F \subseteq L \subseteq K$ is an intermediate field, then $L = K^{\text{Gal}(K/L)}$.
(2): Suppose that $H$ is normal in $G$. Then $L$ is Galois over $F$ by (1), so $L$ is $G$-stable.
Hence $r : G \to \text{Gal}(L/F)$ is a well-defined surjective group homomorphism. The kernel of this map is
\[\begin{aligned} \ker r &= \\{\varphi \in G : \varphi| _ L = 1 _ L\\} \\\\ &= \text{Gal}(K/L) \\\\ &= H \end{aligned}\]Then by the first isomorphism theorem,
\[G/(\ker r) = G/H \cong \text{Gal}(L/F)\]as required.
@important~ (main theorem)
Examples
Suppose:
- $K/F$ is a Galois extension
- $\text{Gal}(K/F) \cong C _ {60}$
How many intermediate fields are there between $K$ and $F$?
Since $G := \text{Gal}(K/F)$ is cyclic, it has exactly one subgroup for each divisor of $60$. Since $60 = 2^2 \times 3 \times 5$, there are 12 intermediate fields.
@exam~ @example~
Can you give an @example of a field extension $K/F$ with infinitely many subfields?
Let:
- $F = \mathbb F _ p(t _ 1, t _ 2)$, i.e. the field of fractions of $\mathbb F _ p[t _ 1, t _ 2]$
- $K = F(\alpha, \beta)$, where:
- $\alpha$ is a root of $x^p - t _ 1$
- $\beta$ is a root of $x^p - t _ 2$
Then $K/F$ is a field extension. Now consider intermediate extensions $L = F(\alpha + \lambda \beta)$ for $\lambda \in F$.
Note that as $F$ is infinite, we may consider an infinite number of fields $F(\alpha + \lambda \beta)$, so it suffices to show that
\[F(\alpha + \lambda \beta) \ne F(\alpha + \mu \beta)\]for distinct $\lambda, \mu \in F$
Suppose for a contradiction that $F(\alpha + \lambda \beta) = F(\alpha + \mu \beta)$. Then $\alpha + \mu \beta \in F(\alpha + \lambda \beta)$, so
\[\begin{aligned} (u - \lambda) \beta &= (\alpha - \alpha) + (\mu - \lambda)\beta \\\\ &= (\alpha + \mu \beta) - (\alpha + \lambda \beta) \\\\ &\in F(\alpha + \lambda \beta) \end{aligned}\]This implies $\beta \in F(\alpha + \lambda \beta)$, as $u - \lambda$ is an element of $F$.
This implies also that $\alpha = \alpha + \lambda \beta - \lambda \beta \in F(\alpha + \lambda \beta)$.
Thus $F(\alpha + \lambda \beta) = F(\alpha, \beta)$. But this is impossible as
\[(\alpha + \lambda \beta)^p = \alpha^p + \lambda^p \beta^p = t_1 + \lambda^p t_2 \in F\]and therefore $m _ {F, a + \lambda \beta}(x) = x^p - (t _ 1 + \lambda^p t _ 2)$, so:
\[[F(\alpha + \lambda \beta) : F] = p\]but
\[[F(\alpha + \lambda \beta) : F] = [F(\alpha, \beta) : F] = p^2\]and $p \ne p^2$.
So each $F(\alpha + \lambda \beta)$ is distinct, and so there are infinitely many subfields.
@exam~