Artificial Intelligence MT24, Online search
Flashcards
Basic definitions
A typical search-based agent in an environment knows the following:
- A set of states $S$
- An initial state $s$, where the agent starts
- Possible actions, described by a function $\mathbf{Actions}(s)$ which returns the set of actions applicable to state $s$
- A transition model, given by a successor function $\mathbf{Result}(s, a)$ which returns the state obtained by applying action $a$ to state $s$
- Goal test: A function for checking whether a state is a goal
- Path cost: A function assigning a value $\mathbf{pc}(p)$ to each path $p = s _ 0, a _ 1, s _ 1, a _ 2, \ldots$ and so on.
What assumption do you drop in order to model an online agent?
$\mathbf{Result}(s, a)$ is not known in advance.
An online agent models the search space via:
- A set of states $S$
- An initial state $s$, where the agent starts
- Possible actions, described by a function $\mathbf{Actions}(s)$ which returns the set of actions applicable to state $s$
- Goal test: A function for checking whether a state is a goal
- Path cost: A function assigning a value $\mathbf{pc}(p)$ to each path $p = s _ 0, a _ 1, s _ 1, a _ 2, \ldots$ and so on.
and where $\mathbf{Result}(s, a)$ is not known in advance. What assumption is needed so that online agents are useful?
The state space is safely explorable, i.e. from every reachable state, some goal state can be reached.
Online depth-first search
Describe the @algorithm used for an online depth-first search algorithm.
# Global variables
result: a table indexed by state and action, initially empty
untried: a table listing, for each state, the actions not yet tried
unbacktracked: a table listing, for each state, the untried backtracks (i.e. previous states we can return to)
s _ prev, a _ prev: the previous state and action, initially null.
function OnlineDFSAgent(s) returns an action:
inputs: s, the current state
if GoalTest(s):
# We have finished
return
if s is a new state:
# We can only determine the actions of a state when we are in that state since the search is online
untried[s] = Actions(s)
if s _ prev != null:
# Fill in the details for where taking a _ prev in s _ prev ends up
result[s _ prev, a _ prev] = s
add s _ prev to the front of unbacktracked[s]
if untried[s] is empty:
# We've not reached the goal and there's nothing left to try
# Therefore we need to backtrack
if unbacktracked[s] is empty:
# In this case we've hit a dead end
return stop
else:
# Take an action which backtracks
a = an action such that result[s, a] is Pop(unbacktracked[s])
else:
# We've not reached the goal but there's still things left to try
# Choose an untried action
a = Pop(untried[s])
s _ prev = s
return a
Show how online depth-first search would enter the dead-end and then reverse out assuming that it moves up from this position:
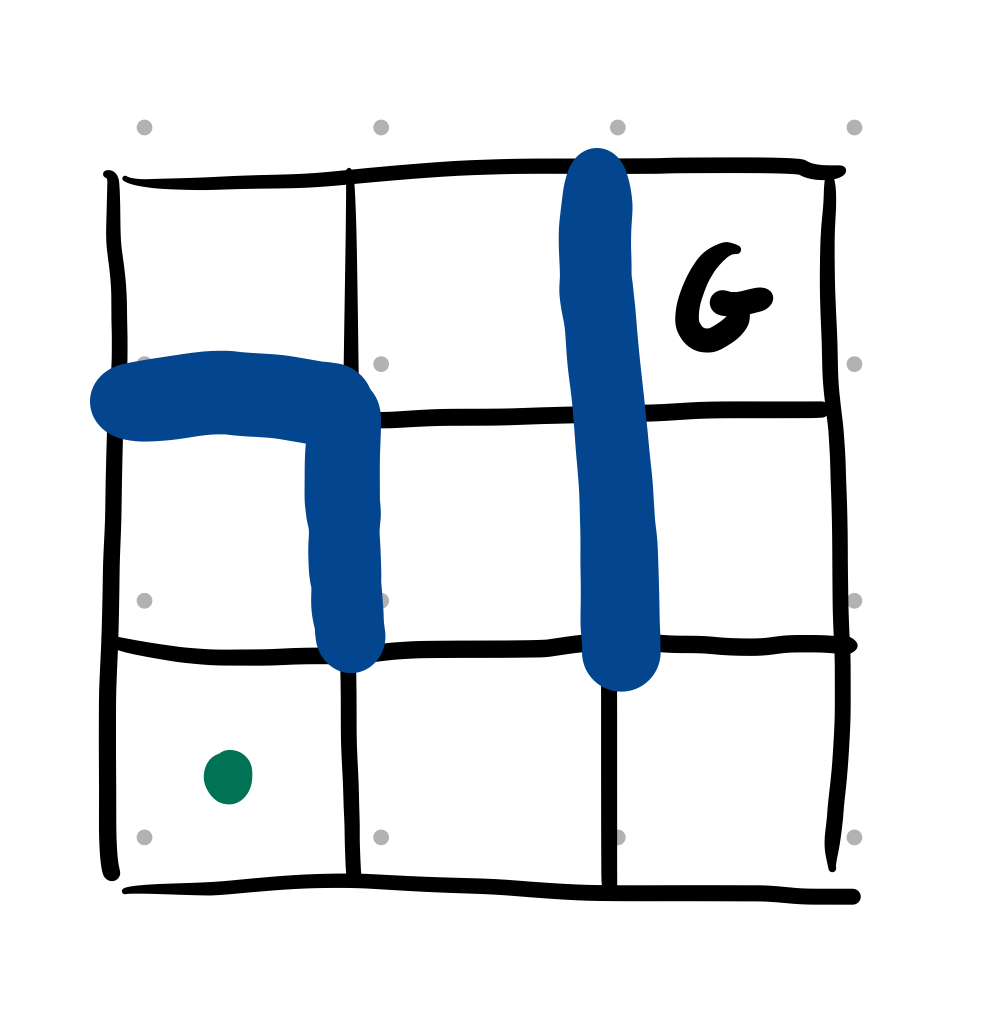

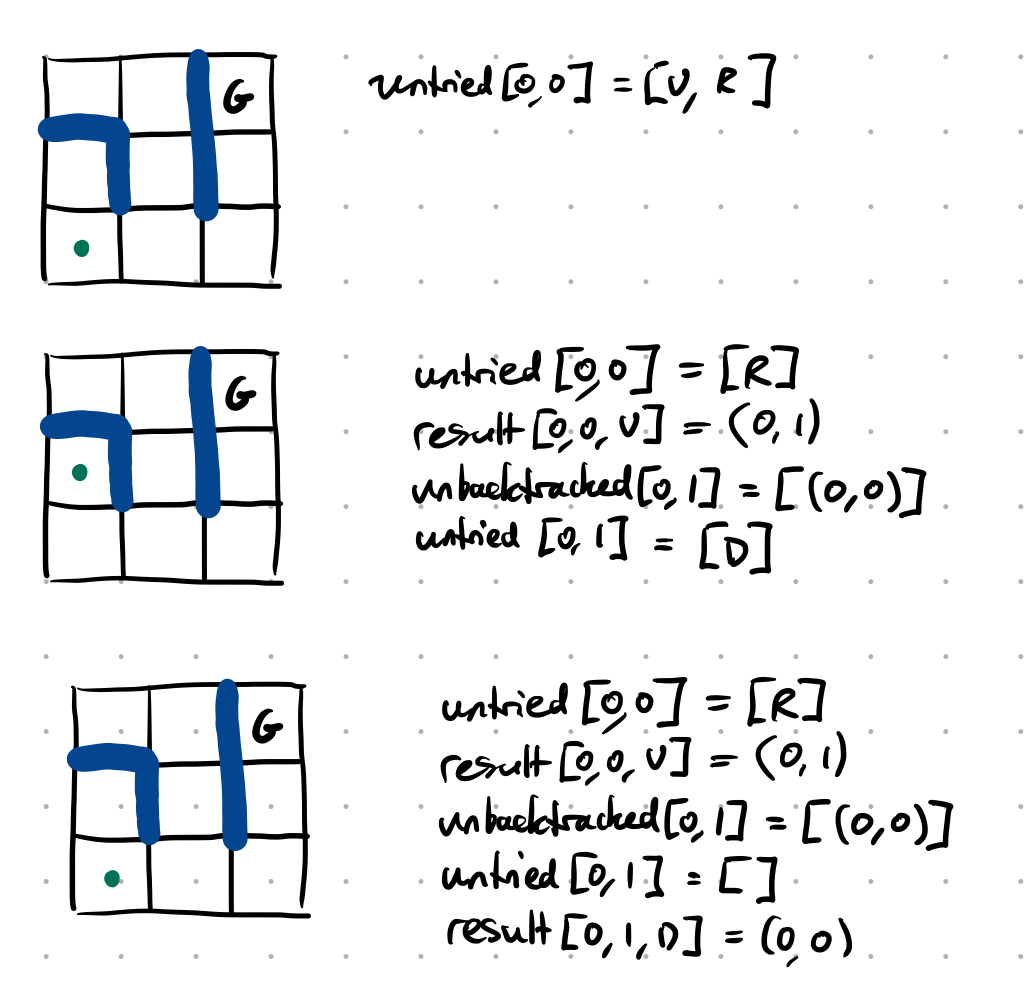
@example~
LRTA*
Describe the $\mathbf{LRTA}^\ast$ (learning real-time $A^\ast$) @algorithm and explain its purpose.
The main purpose of $\mathbf{LRTA}^\ast$ is to explore an unknown environment, making use a heuristic to guide the search.
# Global variables
result: a table indexed by state and action, initially empty
H: a table of cost estimates indexed by state, initially empty
s _ prev, a _ prev: the previous state and action, initially null
# h is a heuristic estimating the cost
function LRTAAgent(s) returns an action:
inputs: s, a percept that identifies the current state
# If we hit a goal node then stop
if GoalTest(s):
return stop
# Set our initial estimate for this state using the heuristic
if s is a new state (not in H):
H[s] = h(s)
# If there is a predecessor, note down how we got to the current state
# and update our estimate of the cost for that previous state by setting
# it to the minimum over all costs of successor states
if s _ prev != null:
result[s _ prev, a _ prev] = s
H[s _ prev] = minimum cost over any action a _ candidate for LRTA-Cost(s _ prev, a _ candidate, result[s _ prev, a _ candidate], H)
# Pick the action which leads to a state of least cost
a _ next = argmin over a _ candidate actions LRTA-Cost(s, a _ candidate, result[s, a _ candidate], H)
s _ prev = s
return a _ next
function LRTA-Cost(s _ 0, a _ candidate, s _ 1, H) returns a cost estimate:
if s _ 1 is undefined:
# If we know nothing about the successor state because we haven't
# figured it out yet, a good estimate is that the cost is just the
# heuristic applied to the current state
return h(s _ 0)
else:
return c(s _ 0, a _ candidate, s _ 1) + H[s _ 0]
It may be helpful to contrast to the online DFS agent:
# Global variables
result: a table indexed by state and action, initially empty
untried: a table listing, for each state, the actions not yet tried
unbacktracked: a table listing, for each state, the untried backtracks (i.e. previous states we can return to)
s _ prev, a _ prev: the previous state and action, initially null.
function OnlineDFSAgent(s) returns an action:
inputs: s, the current state
if GoalTest(s):
# We have finished
return
if s is a new state:
# We can only determine the actions of a state when we are in that state since the search is online
untried[s] = Actions(s)
if s _ prev != null:
# Fill in the details for where taking a _ prev in s _ prev ends up
result[s _ prev, a _ prev] = s
add s _ prev to the front of unbacktracked[s]
if untried[s] is empty:
# We've not reached the goal and there's nothing left to try
# Therefore we need to backtrack
if unbacktracked[s] is empty:
# In this case we've hit a dead end
return stop
else:
# Take an action which backtracks
a = an action such that result[s, a] is Pop(unbacktracked[s])
else:
# We've not reached the goal but there's still things left to try
# Choose an untried action
a = Pop(untried[s])
s _ prev = s
return a
@State the time complexity of the $\mathbf{LRTA}^\ast$ agent in a finite state space with $n$ states.
Show how the $\mathbf{LRTA}^\ast$ (learning real-time $A^\ast$) search would begin its search, assuming that the heuristic $h$ being used is the length of the shortest path. Assume that it luckily picks actions that end up moving it closer to the goal.

(although note that in reality the length of the shortest path couldn’t be used as the heuristic since by assumption the shortest path is not known ahead of time).

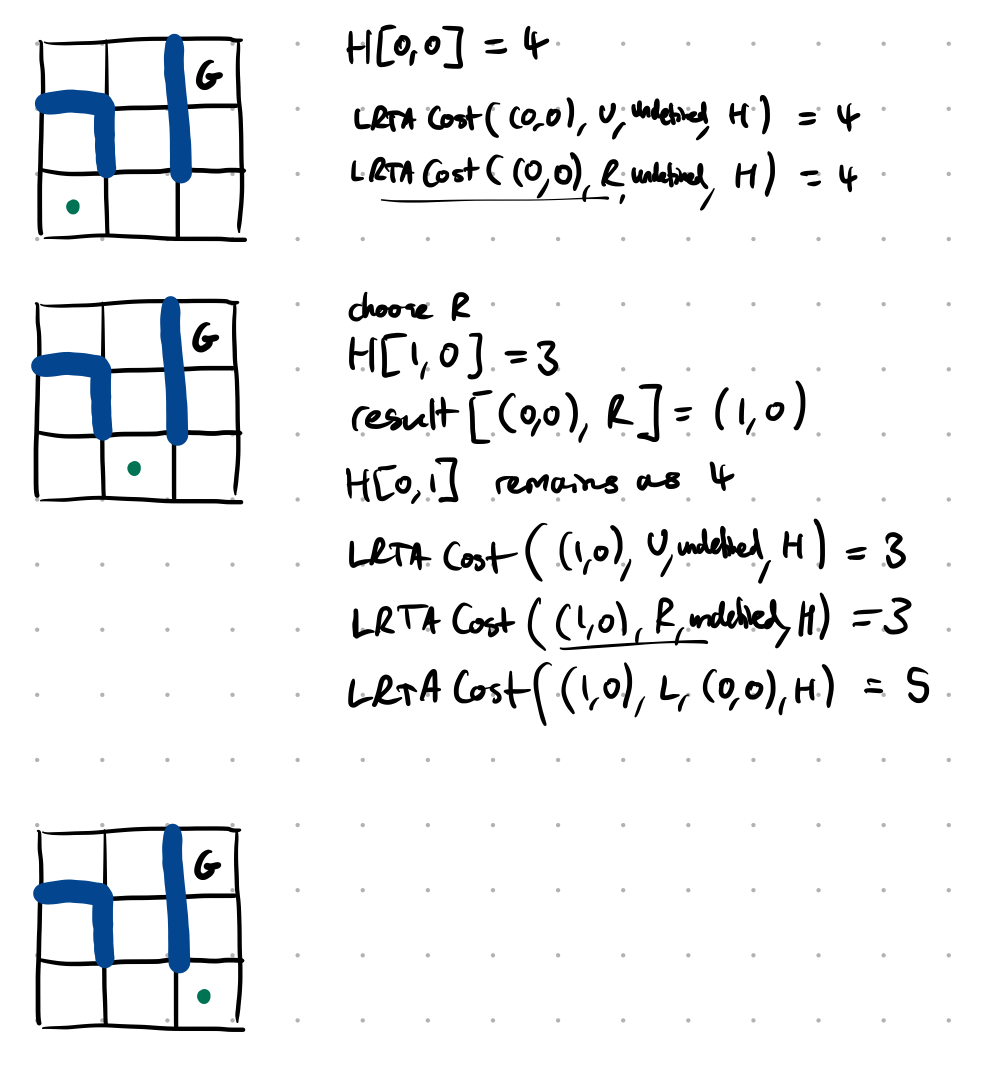
(oops, the line that says “$H[0, 1]$ remains as $4$” should really be $H[0, 0]$ remains as $4$, since the minimum is just over the singleton $\lbrace \mathbf{LRTA}\text{-}\mathbf{Cost}((0, 0), R, (1, 0), H)\rbrace$ which equals $4$)
@example~