Computer Vision MT25, Neural rendering
Flashcards
The rendering equation
@State and @visualise the rendering equation for determining how much light $L _ o$ of wavelength $\lambda$ is leaving a point $x$ in the direction of $\omega _ 0$ at time $t$.
where $L _ e$ is the emitted radiance and $L _ r$ is the reflected radiance, defined by
\[L _ r(x, \omega _ 0, \lambda, t) = \int _ \Omega f _ i(x, \omega _ i, \omega _ o, \lambda, t) L _ i(x, \omega _ i, \lambda, t) (\omega _ i \cdot \pmb n) \text d\omega _ i\]and:
- $f _ i$ is the bidirectional reflectance distribution function (BRDF), which describes the intensity that the reflected light from direction $\omega _ i$ reflects to the observer
- $L _ i$ is the incoming radiance at $x$ from direction $\omega _ i$
- $\pmb n$ is the surface norm at $x$
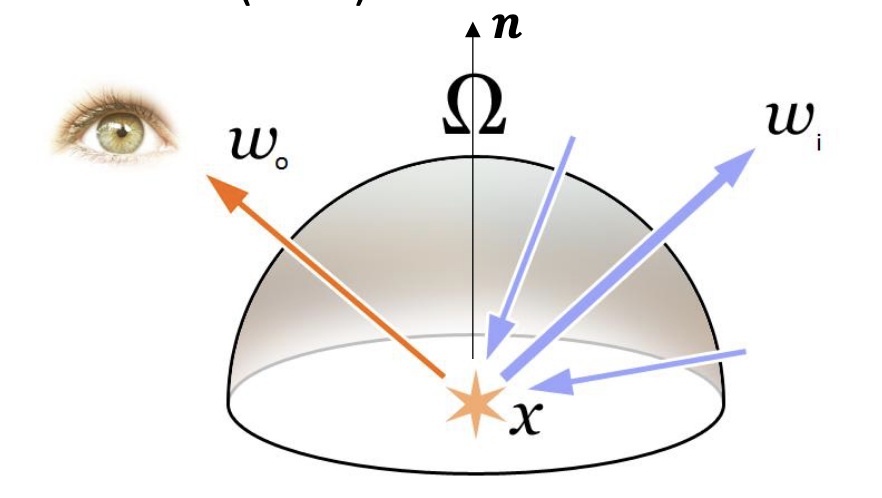
The rendering equation for determining how much light $L _ o$ of wavelength $\lambda$ is leaving a point $x$ in the direction of $\omega _ 0$ at time $t$ is given by
\[L _ o(x, \omega _ 0, \lambda, t) = L _ e(x, \omega _ o, \lambda, t) + L _ r(x, \omega _ o, \lambda, t)\]
where $L _ e$ is the emitted radiance and $L _ r$ is the reflected radiance, defined by
\[L _ r(x, \omega _ 0, \lambda, t) = \int _ \Omega f _ i(x, \omega _ i, \omega _ o, \lambda, t) L _ i(x, \omega _ i, \lambda, t) (\omega _ i \cdot \pmb n) \text d\omega _ i\]
and:
- $f _ i$ is the bidirectional reflectance distribution function (BRDF), which describes the intensity that the reflected light from direction $\omega _ i$ reflects to the observer
- $L _ i$ is the incoming radiance at $x$ from direction $\omega _ i$
- $\pmb n$ is the surface norm at $x$
@State the definition of $f _ r$ in terms of the $L _ r$ and the surface normal $\pmb n$, and state three properties that need to be true about any $f _ r$.
- Positivity: $f _ r(\omega _ i, \omega _ r) > 0$
- Reciprocity: $f _ r(\omega _ i, \omega _ r) = f(\omega _ r, \omega _ i)$
- Energy conservation: $\forall w _ i, \int _ \Omega f _ r(\omega _ i \cdot \pmb n) \text d\omega r \le 1$
Neural radiance fields
@State the typical problem setup in neural radiance fields.
- Input: Collection of images of some scene
- Learning: Mapping coordinates $(x, y, z)$ to colour and occupancy
- Output: Rendering of scene from new viewpoints
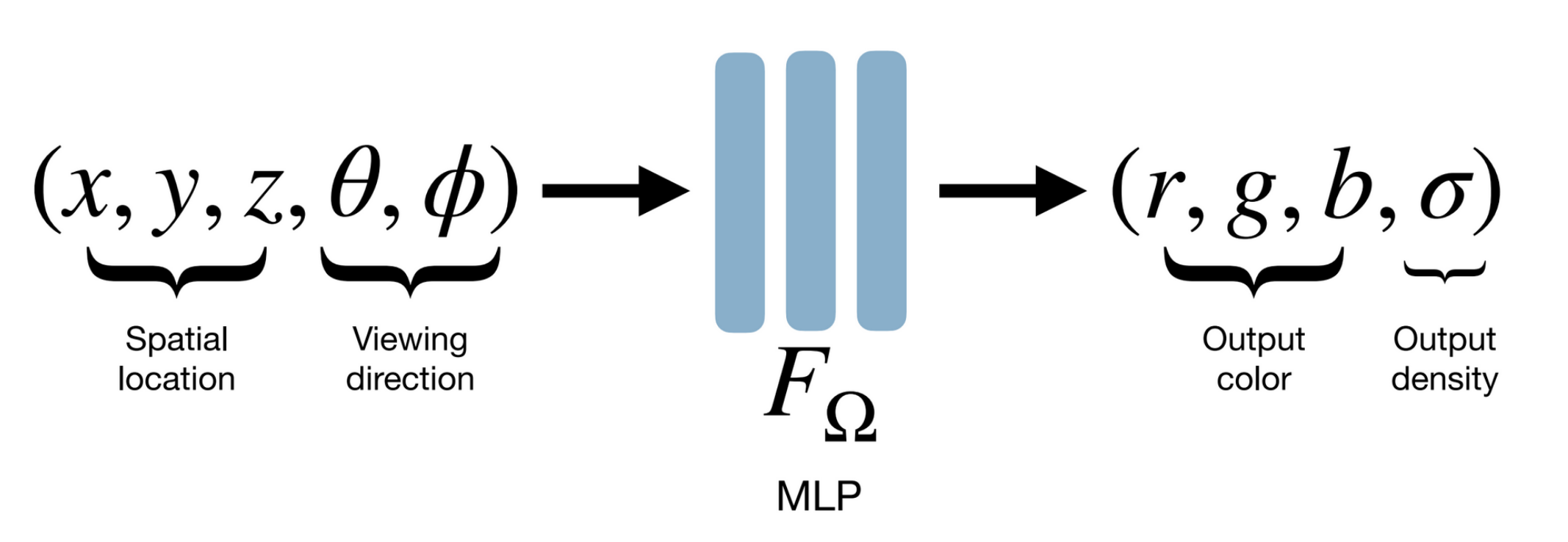
In neural radiance fields, the typical setup is:
- Input: Collection of images of some scene
- Learning: Mapping coordinates $(x, y, z)$ to colour and occupancy
- Output: Rendering of scene from new viewpoints
How is the loss determined?
We render an image using the model via direct volume rendering, and compare this to a ground truth image.
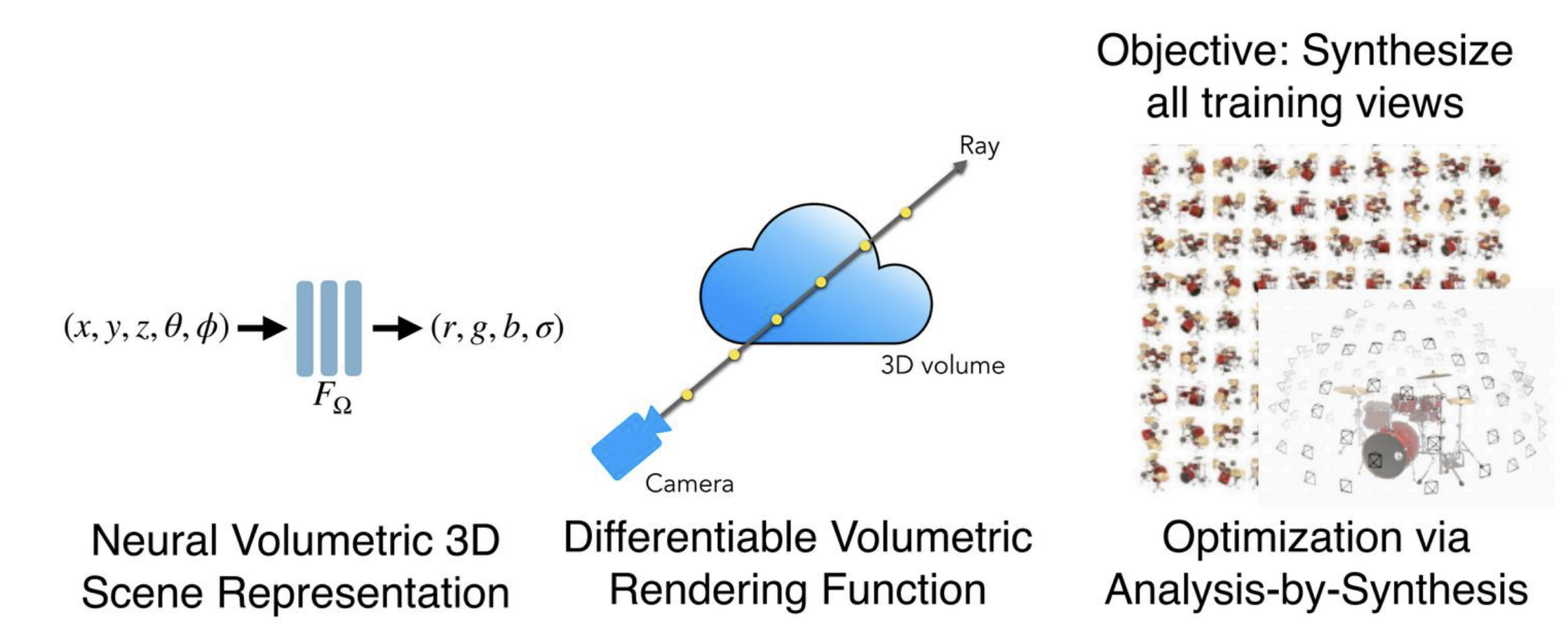
@State the equation used to determine the colour of a point corresponding to a ray emerging from the camera $r(t) = o + td$ when performing direct volume rendering.
where the sum is taken over some finite amount of steps along the ray, and:
- $T _ i$ is the visibility of that point, given by a product of previous opacities $T _ i = \prod^{i - 1} _ {j = 1}(1 - \alpha _ i)$
- $\alpha _ i$ is the opacity of a point, given by $\alpha _ i = 1 - e^{-\sigma _ i \Delta _ t}$
- state the rendering equation
- define the brdf
- define a neural radiance field
- how is the loss computed for a nerf? volume renderer
- how does direct volume rendering work