Course - Galois Theory HT25
An introductory course on Galois Theory, focussed on building the theory to the point where we can prove the insolubility of quintics by radicals (i.e. there is no “quintic formula” like the “quadratic formula”). The core observation of Galois theory is a remarkable correspondence between field extensions (i.e. $\mathbb Q$ is a field, if you “add” $\sqrt 2$ as an element to $\mathbb Q$, you have the extension $\mathbb Q[\sqrt 2]/\mathbb Q$) and the so-called Galois group of the field extension, which is (in some specific way) the set of “symmetries” of the field extension.
This course actually answered some questions I had from studying Further Maths at A-level, like the relevance of the [[Further Maths - Roots of Polynomials]]A topic and why complex numbers $a + bi$ seemed very similar to something like $a + b\sqrt 2$ (they’re both vector spaces containing conjugation as a linear map).
- Course Webpage
- Lecture Notes:
- Lecture notes by Prof. Damian Rössler (easier to follow)
- Old lecture notes by Prof. Konstantin Ardakov (more concise)
- My notes here are based primarily on the old lecture notes (oops).
- Other courses this term: [[Courses HT25]]U
- Relevant textbooks:
Notes
- [[Notes - Galois Theory HT25, Background from group theory]]U
- [[Notes - Galois Theory HT25, Group actions]]U
- [[Notes - Galois Theory HT25, Symmetric functions]]U
- [[Notes - Galois Theory HT25, Fields and field extensions]]U
- [[Notes - Galois Theory HT25, Galois groups and Galois extensions]]U
- [[Notes - Galois Theory HT25, Bounds on the size of the Galois group]]U
- [[Notes - Galois Theory HT25, Separability]]U
- [[Notes - Galois Theory HT25, Normality]]U
- [[Notes - Galois Theory HT25, Artin’s lemma]]U
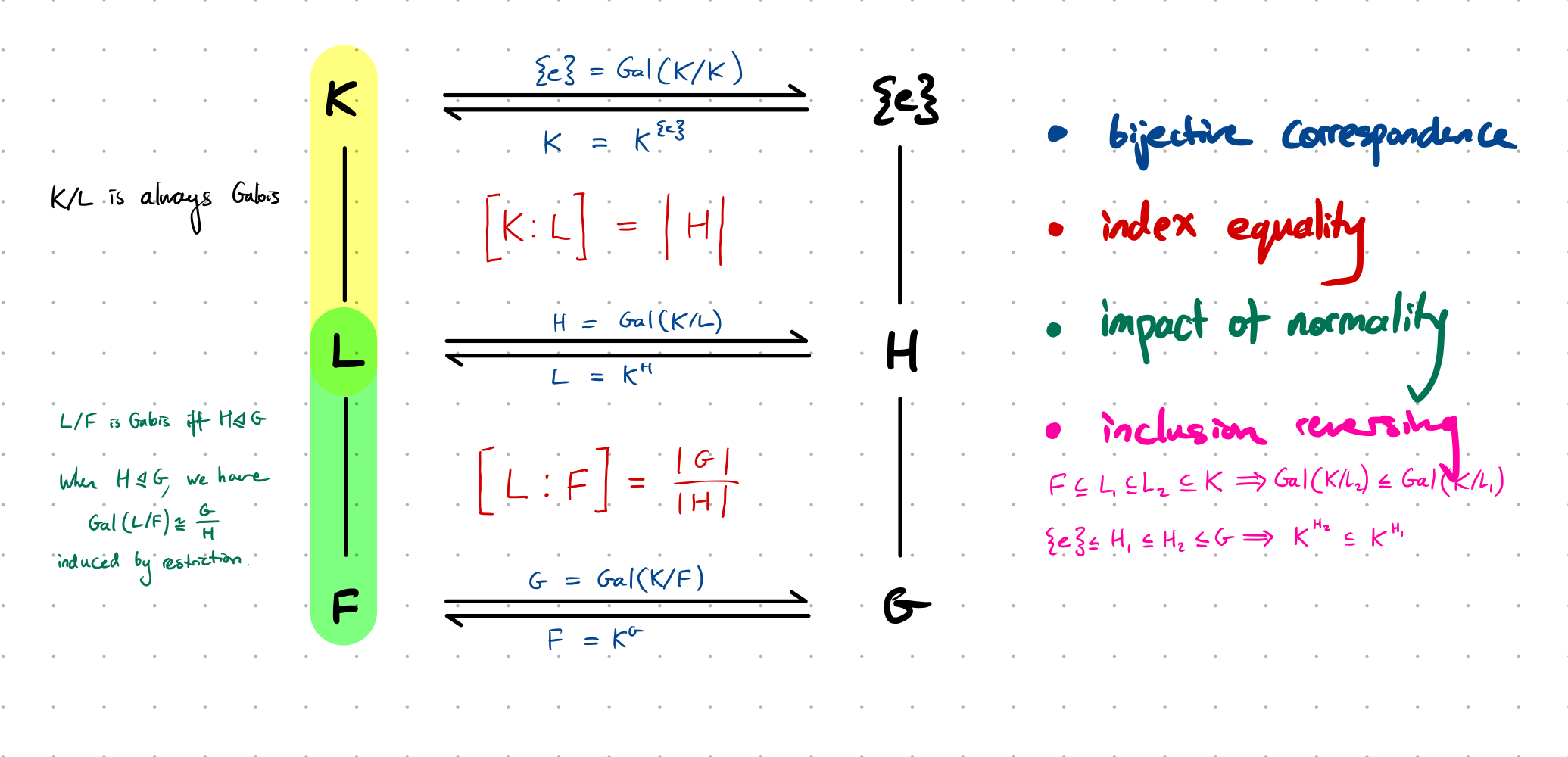
- [[Notes - Galois Theory HT25, Main theorems of Galois theory]]U ⭐️
- [[Notes - Galois Theory HT25, Computing the Galois group]]U ⭐️
- [[Notes - Galois Theory HT25, Primitive element theorem]]U
- [[Notes - Galois Theory HT25, Solvable groups]]U
- [[Notes - Galois Theory HT25, Solvability by radicals]]U
- [[Notes - Galois Theory HT25, Cyclotomic extensions]]U
- [[Notes - Galois Theory HT25, Kummer extensions]]U
- [[Notes - Galois Theory HT25, Determinant and discriminant]]U
- [[Notes - Galois Theory HT25, Cubic equations]]U
- [[Notes - Galois Theory HT25, Quartic equations]]U
- [[Notes - Galois Theory HT25, Quintic equations]]U
- [[Notes - Galois Theory HT25, Finite fields]]U
- [[Notes - Galois Theory HT25, Misc]]U
Related notes
The Part A [[Course - Rings and Modules HT24]]U is a prerequisite, especially:
- [[Notes - Rings and Modules HT24, Basic definitions for rings]]U
- [[Notes - Rings and Modules HT24, Ring quotients]]U
- [[Notes - Rings and Modules HT24, Ideals]]U
- [[Notes - Rings and Modules HT24, Eisenstein’s criterion]]U
- [[Notes - Rings and Modules HT24, Factorisation in polynomial rings]]U
- [[Notes - Rings and Modules HT24, Factorisation]]U
- [[Notes - Rings and Modules HT24, Fields]]U
- [[Notes - Rings and Modules HT24, Polynomial rings]]U
- [[Notes - Rings and Modules HT24, Structure theorems]]U
The Prelims courses [[Course - Groups and Group Actions HT23]]U and [[Course - Groups and Group Actions TT23]]U are also very relevant:
- [[Notes - Groups HT23, Normal subgroups]]U
- [[Notes - Groups TT23, Group actions]]U
- [[Notes - Groups TT23, Orbits and stabilisers]]U
- [[Notes - Groups TT23, Quotient groups]]U
And occasionally results from the linear algebra courses [[Course - Linear Algebra I MT22]]U, [[Course - Linear Algebra II HT23]]U and [[Course - Linear Algebra MT23]]U are used.
Problem Sheets
- [[Problem Sheet - Galois Theory HT25, I]]?
- [[Problem Sheet - Galois Theory HT25, II]]?
- [[Problem Sheet - Galois Theory HT25, III]]?
- [[Problem Sheet - Galois Theory HT25, IV]]?
- Sheet 1, partial solutions
- Sheet 2
- Sheet 3, partial solutions
- Sheet 4, partial solutions
